Модельная система поддержки принятия решений для управления информационными ресурсами вуза
Авторы
Аннотация
Статья посвящена проблеме качества обслуживания в библиотеках вуза. Предложена модельная система управления качеством обслуживания, состоящая из трех комплексов моделей, позволяющих имитировать процесс обслуживания, предвидеть результаты принимаемых управляющих решений и выбрать наилучшее из них. Предложены экономико-математические модели оценки качества принимаемых решений. Модели разработаны на основе аппарата теории массового обслуживания. Показаны области применения каждого из видов моделей. Продемонстрирован процесс разработки проекта штатного расписания, позволяющий оптимальным образом определить количество персонала, необходимого для обслуживания читателей библиотеки вуза в различные периоды времени.
Ключевые слова
оптимизация; библиотека вуза; вероятность; теория массового обслуживания, автоматизированная система моделей, игровая модель.
Рекомендуемая ссылка
No items found. Модельная система поддержки принятия решений для управления информационными ресурсами вуза // Современные технологии управления. ISSN 2226-9339. — №4 (16). Номер статьи: 1603. Дата публикации: 08.04.2012. Режим доступа: https://sovman.ru/article/1603/
Authors
Abstract
Keywords
Suggested citation
No items found. // Modern Management Technology. ISSN 2226-9339. — №4 (16). Art. # 1603. Date issued: 08.04.2012. Available at: https://sovman.ru/article/1603/
В современный период развития постиндустриальной экономики заостряются вопросы использования знаний в различных аспектах управления народным хозяйством. Эти обстоятельства диктуют необходимость повышения качества подготовки специалистов вузами, что, в свою очередь, требует повышения оперативности обслуживания студентов и научных работников системы высшего образования информационными ресурсами. В этой связи, в настоящее время стоит проблема повышения качества управления библиотеками вуза, играющими решающую роль в накоплении и приращении знаний.
Все это влечет за собой предъявление библиотекам высоких требований к качеству обслуживания читателей. Возникающие при этом проблемы выдвигают необходимость всестороннего анализа всей совокупности относящихся к библиотеке вопросов. Это обусловлено тем, что все аспекты работы библиотеки взаимосвязаны, и она функционирует как единое целое. Эти обстоятельства наряду с повышением требований к качеству высшего образования ставят акцент на управлении этим качеством и его совершенствование на основе научно обоснованного математического аппарата.
Современные подходы не позволяют оптимизировать проблемы качества обслуживания посетителей в библиотеке вуза. Решение данной проблемы представляется посредством применения информационных систем, основанных на применении математических методов и разработок. Предлагается комплекс экономико-математических моделей, позволяющих моделировать и оптимизировать процессы, протекающие в библиотеке вуза.
Ввиду такого подхода разработана модельная система (рис. 1).
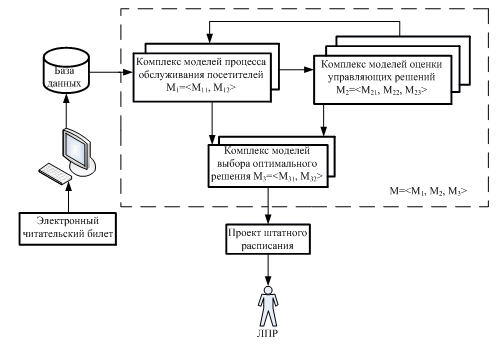
Рис. 1. Модельная система моделей управления качеством обслуживания
В предложенную систему входит комплекс моделей управления качеством обслуживания M=<M1, M2, M3>, где M1 – комплекс моделей, описывающий процесс обслуживания читателей, M2 – комплекс моделей оценки управляющих решений, М3 – комплекс моделей выбора оптимального решения.
Комплекс моделей процесса обслуживания читателей М1=<М11, М12> состоит из двух моделей, таких как М11 – модель построения закона распределения случайной величины плотности потока читателей, М12 – имитационная модель.
Имитационная модель М12 позволяет воспроизводить процесс подачи заявок читателями библиотеки вуза и процесс их обслуживания. В роли входных переменных выступает величина интенсивности поока читателей. Выходами системы являются показатели качества обслуживания, описанные виде вектора 
, компонентами которого являются: показатель неравномерности загрузки мест обслуживания 
, среднее время нахождения в очереди 
, отклонение длины очереди от заданной длины 
, суммарная заработная плата 
. [5]. В роли управляющих переменных рассматривается вектор 
, где 
– количество точек обслуживания читателей конкретного отдела библиотеки, 
– квалификационный уровень библиотекарей. [2]
Для формального описания процесса принятия решений в статье предложено три вида математических моделей: М21 — модель обслуживания с отказом, М22 — модель обслуживания с ожиданием, М23 — модель обслуживания с ограничением по длине очереди.
Ранее автором предлагалась модель обслуживания с отказом для оценки качества обслуживания, обозначенная М21. [3]. В данной статье расширены результаты, позволяющие углубить возможность моделирования и учесть другие аспекты обслуживания, а именно модели обслуживания с ожиданием М22 и модель с ограничением по длине очереди М23.
Модель массового обслуживания с ожиданием М22 рассматривает такое же множество состояний 
, что и модель М1.Но в такой системе заявка, заставшая все каналы обслуживания занятыми, не покидает систему, а становится в очередь и ожидает, пока не освободится какой-нибудь канал. Ввиду этого система дополняется следующим множеством состояний 
. В результате множество состояний для модели М2 будет выглядеть следующим образом:
, где:
— заняты все n библиотекарей, один посетитель стоит в очереди,
…
— заняты все n библиотекарей, s посетителей стоят в очереди,
…
Выходными сигналами в данной модели являются вероятности состояний системы:
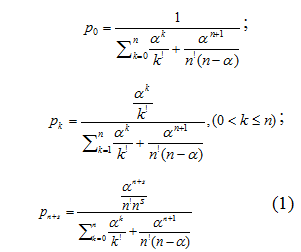
Кроме вероятностей 
на выходе модели М2 получим среднее число заявок, находящихся в очереди:
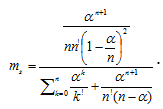
По формуле (1) выполнено численное моделирование для значений переменных n=3 (чел.), 
=17 (мин.) (n – количество точек обслуживания, — время обслуживания), полученных в результате функционирования имитационной модели. Результаты сведены в табл. 1.
Таблица 1
| Количество точек обслуживания |
Вероятность занятости канала Р |
Длина очереди к n-му каналу |
|
1 |
0,196 |
0,209 |
|
2 |
0,238 |
0,064 |
|
3 |
0,192 |
0,015 |
Модель массового обслуживания с ограничением по длинеочереди М23 представляет собой n-канальную систему с ожиданием, в которой количество заявок, стоящих в очереди, ограничено числом m. Множество состояний для данной модели будут иметь вид:
,
где 
— множество состояний, используемое в модели M1 и 
, где:
— заняты все n библиотекарей, один посетитель стоит в очереди,
…
— заняты все n библиотекарей, m посетителей стоят в очереди,
…
Предположим, что заявка, заставшая все каналы занятыми, становится в очередь, только если в ней находится менее m заявок; если же число заявок в очереди равно m (больше m оно и быть не может), то последняя прибывшая заявка в очередь не становится и покидает систему необслуженной.
Выходными сигналами для данной модели будут вероятности состояний системы [1]:
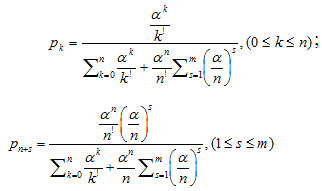; (2)
По формуле (2) выполнено численное моделирование с вариацией значений, результаты которого сведены в табл. 2.
Таблица 2
| Количество точек обслуживания |
Вероятность занятости канала Р |
Длина очереди к n-му каналу |
|
1 |
0,158 |
0,102 |
|
2 |
0,191 |
0,082 |
|
3 |
0,155 |
0,066 |
Для доказательства работоспособности описанных ранее моделей были проведены эксперименты и продемонстрирован процесс их использования для принятия решений. При постановке экспериментов на имитационной модели варьировались значения величины – описывающие количество точек обслуживания читателей и на выходе получены соответствующие значения пропускной способности системы q=1-Vi, где Vi – вероятность отказа точки обслуживания (рис. 2). При проведении экспериментов на моделях, основанных на аппарате теории массового обслуживания, также фиксировались значения величины q (рис. 2).
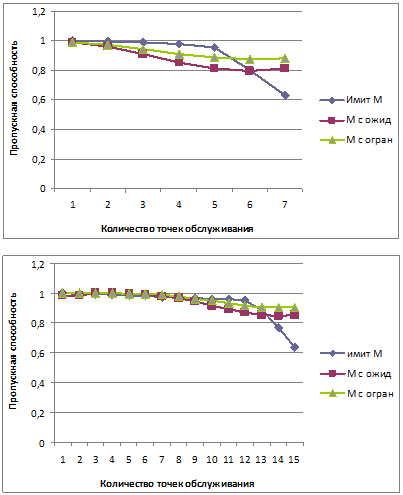
Рис. 2 Результаты функционирования моделей
Таким образом, предложенные модели M22, M23 позволяют с количественной точки зрения оценить целесообразность решений, рекомендуемых в результате функционирования имитационной модели. Сравнительный анализ свидетельствует о том, что результаты моделирования в заданном интервале изменения аргументов различаются не более чем на 10 %.
Модели M1, M2, M3 могут также использоваться как исходные данные для функционирования модели оптимизации.
Как указывалось ранее, в комплекс М входит комплекс моделей выбора оптимального решения М3 и состоит из двух моделей: М31 – экономико-математическая модель поиска оптимальных решений, М32 – игровая модель нахождения компромиссных решений. Данная модель базируется на формальном описании онтоганистической игры Фон-Неймана [4]. В качестве игроков выбраны критерии качества и оптимальные значения количества точек обслуживания () и квалификационного уровня () относительно этих критериев. Задача управления ставится следующим образом: при заданном потоке читателей найти такое значение входных управляемых переменных U, из множества допустимых значений UD, при которой котором критерий качества Pi достигает оптимума:
[2],
где U* — значения вектора 
, являющиеся оптимальным относительно критерия .
В результате взаимодействия трех комплексов моделей был составлен проект штатного расписания работы сотрудников библиотеки вуза. В таблице 3 представлены результаты расчетов, где интенсивность прихода читателей I:
,
где n – количество посещений в определенный месяц, 
– общее рабочее время в месяц (160 час.)
Таблица 3
|
Месяцы |
Количество посещений |
Интенсивность прихода читателей I |
Проект штатного расписания |
|
|
Количество точек обслуживания |
Квалификационный |
|||
|
Январь |
73 |
2,19 |
1, 5, 5 |
2, 3, 7 |
|
Февраль |
82 |
1,95 |
1, 5, 5 |
2, 3, 7 |
|
Март |
67 |
2,38 |
1, 4, 5 |
2, 3, 6 |
|
Апрель |
60 |
2,66 |
1, 4, 5 |
2, 3, 6 |
|
Май |
58 |
2,75 |
1, 4, 5 |
2, 3, 7 |
|
Июнь |
37 |
4,32 |
1, 3, 3 |
2, 2, 5 |
|
Июль |
15 |
10,6 |
1, 2, 2 |
3, 1, 2 |
|
Август |
22 |
7,27 |
1, 2, 2 |
3, 1, 2 |
|
Сентябрь |
111 |
1,44 |
1, 5, 7 |
2, 6, 7 |
|
Октябрь |
92 |
1,73 |
1, 5, 7 |
2, 3, 7 |
|
Ноябрь |
54 |
2,36 |
1, 4, 5 |
2, 3, 6 |
|
Декабрь |
45 |
3,55 |
1, 3, 4 |
1, 2, 6 |
|
Январь |
15 |
10,6 |
1, 2, 2 |
3, 1, 2 |
На рисунке 3 представлено визуальное представление проекта штатного расписания.
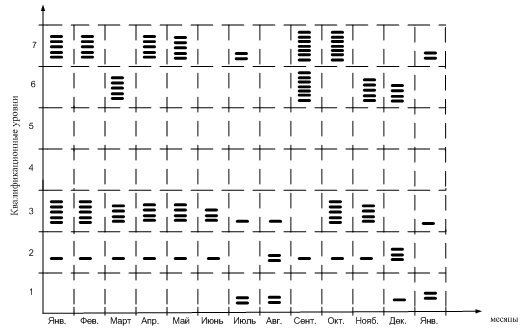
Рис. 3. Проект штатного расписания работы сотрудников библиотеки вуза
На основе предложенного проекта штатного расписания работы библиотеки вуза лицо, принимающее решение может оптимизировать процесс распределения принимаемых управленческих решений в разные периоды времени.
Полученные результаты позволяют сформулировать следующие выводы:
- Предложена модельная система управления качеством обслуживания M=<M1, M2, M3>, состоящая из трех комплексов, позволяющих имитировать процесс обслуживания, предвидеть последствия принимаемых управляющих решений и выбрать наилучшее из них.
- Продемонстрирована оценка качества принимаемых решений посредством вычисления вероятностей состояний на базе системы массового обслуживания.
- Произведен сравнительный количественный анализ решений, принимаемых имитационной и моделями, основанными на теории массового обслуживания.
- Продемонстрирован проект штатного расписания работы библиотеки вуза, созданный на базе моделирования.
Читайте также
Библиографический список
- Вентцель Е.С. Теория вероятностей. – М. : Изд-во «Наука», 1969. – 564 с.
- Комплекс экономико-математических моделей оценки качества управления информационными ресурсами / Е.Д. Стрельцова, М.О. Яблонская, О.Ф. Ковалев // Вестник Адыгейского университета. – 2011. — № 2. – С. 181-185
- Модельный подход к оценке качества управления информационными ресурсами вуза // European Social Science Journal. — 2011. — № 11 (14). — С. 65-71.
- Вентцель Е.С. Введение в исследование операций. – М. : «Сов. радио», 1964. – 384 с.
- Экономико-математическое моделирование процессов обслуживания библиотеки вуза / Е.Д. Стрельцова, М.О. Яблонская, О.Ф. Ковалев // Государственное регулирование экономики: проблемы и перспективы : коллект. монография тр. преподавателей, докторантов, аспирантов и студентов кафедры теории и практики гос. регулирования экономики ЮФУ / Юж. фед. ун-т. – Ростов н/Д : Изд-во «Эверест», 2011. – С. 56-59.
