Формирование эконометрического инструментария исследования инвестиционной привлекательности отраслевых комплексов
Formation of econometric research toolkit investment attractiveness industrial complexes
Авторы
Аннотация
В данной работе рассматриваются основные положения эконометрического исследования инвестиционных процессов в условиях отраслевого разделения труда, лежащего в основе формирования комплексного инструментария оценки, прогнозирования и моделирования инвестиционной привлекательности отраслевых комплексов.
Ключевые слова
Финансовый менеджмент, инвестиционный менеджмент, инвестиции, инвестиционная ситуация, инвестиционная привлекательность, инвестиционный потенциал, инвестиционный риск, прогнозирование инвестиционных преференций (ожиданий), моделирование инвестиционной ситуации.
Рекомендуемая ссылка
Перцухов Виктор Иванович. Формирование эконометрического инструментария исследования инвестиционной привлекательности отраслевых комплексов // Современные технологии управления. ISSN 2226-9339. — №10 (22). Номер статьи: 2206. Дата публикации: 08.10.2012. Режим доступа: https://sovman.ru/article/2206/
Authors
Abstract
This paper provides an outline of the econometric studies of investment processes in terms of the sectoral division of labor, which is the basis of forming an integrated assessment tools, forecasting and modeling of investment attractiveness of industrial complexes.
Keywords
Financial management, investment management, investment, investment situation, investment attraction, investment-nual capacity, investment risk, forecasting investment preferences (expectations), modeling investment situation.
Suggested citation
Pertsuhov Viktor Ivanovich. Formation of econometric research toolkit investment attractiveness industrial complexes // Modern Management Technology. ISSN 2226-9339. — №10 (22). Art. # 2206. Date issued: 08.10.2012. Available at: https://sovman.ru/article/2206/
Современные тенденции развития социально-экономических отношений в государстве предусматривают необходимость формализации не только эффективных стратегических подходов построения общественных отношений, не менее важными представляются пути развития оптимальных тактических методов управления социально-экономическими процессами, а также инструментарий исследования характера данных процессов, степени их воздействия на качество жизни [1].
Одними из наиболее важных социально-экономических процессов, определяющих пути развития социального общества, безусловно, являются инвестиционные процессы. Степень проявления последних во многом обусловлена характером инвестиционного поведения потенциального инвестора, которое определяется обстоятельствами, характеризующими как сам объект интересов инвестора, так и условия, в которых он функционирует. В силу этого особую важность приобретает инструментарий, которым руководствуется инвестор при оценке целесообразности ведения активной инвестиционной политики в отношении того или иного объекта его интересов [2,3].
В данной работе изложены основные положения исследования инвестиционных процессов, объектом приложения которых выступает совокупность отраслевых комплексов. Основной задачей этого исследования представляется разработка инструмента оценки степени инвестиционной привлекательности отраслевых комплексов.
Процедура моделирования инвестиционной привлекательности отраслевых комплексов предусматривает последовательную реализацию ряда операций [4].
I этап. Построение базы данных и изучение их свойств.
База данных, используемая для выявления скрытых математических зависимостей, состоит из двух элементов: наблюдений (регистров) и переменных.
Поскольку в данной работе исследуется инвестиционная политика хозяйствующих субъектов, проявляющаяся, в частности, сквозь призму воздействия отраслевых факторов, в рамках данного исследования была сформирована база данных, содержащая информацию о состоянии и динамике развития отраслевых комплексов, составляющих инфраструктуру народного хозяйства Российской Федерации.
Данные отраслевые комплексы рассматриваются в качестве наблюдений (регистров) во вновь формируемой базе данных. В качестве переменных базы данных выступают показатели состояния отраслей, описывающие качественные и количественные характеристики их деятельности.
Основными источниками формируемой базы данных являются официальные материалы Государственного комитета статистики РФ, а также производные от них.
Максимальный уровень предсказательной силы вновь разрабатываемой модели напрямую зависит от глубины исследования. В ходе моделирования инвестиционной привлекательности отраслевых комплексов был использован четырнадцатилетний период исследования (1995-2008 гг.), поскольку для этого периода новейшей истории Российской Федерации характерно проявление устойчивых тенденций стабилизации финансовых и экономических преференций, т.е. для этого периода появилась возможность создания адекватных прогнозов и моделей развития как экономики Российской Федерации в целом, так и отдельных субъектов финансового (инвестиционного) рынка Российской Федерации.
Поскольку для сформированной базы данных характерна разнородность и разобщённость цифрового материала, проводится операция стандартизации базы данных.
Заканчивается I этап изучением дескриптивных статистик, характерных для вновь созданной базы данных, и построением корреляционных матриц с целью выявления внутренних связей между переменными, составляющих базу данных.
II этап. Формирование перечня параметров, используемых для построения модели оценки инвестиционной привлекательности отраслевых комплексов.
Моделирование индекса инвестиционной привлекательности отраслевых комплексов должно быть ориентировано на возможность учёта различных, часто разнонаправленных характеристик, описывающих состояние отраслевых комплексов и тенденции их развития. В связи с этим представление индекса инвестиционной привлекательности отраслевых комплексов в качестве отдельной линейной или нелинейной модели не представляется возможным, поскольку данная модель предполагает жёсткую конкретизацию индикативной цели моделирования и (или) чёткое разграничение потенциальных пользователей модели, т.е. ориентирование модели на приоритеты последних [4].
Для того чтобы достичь максимальной универсальности формируемой модели, инвестиционную привлекательность следует рассматривать в качестве обобщающей характеристики сочетания трёх базовых векторов, в полной мере описывающих всевозможные приоритеты потенциального инвестора:
- вектор экономического роста – характеризует тенденции социально-экономического развития отраслевых комплексов;
- вектор доходности – характеризует степень эффективности (результативности) функционирования отраслевых комплексов;
- вектор риска – характеризует степень вариабельности основных индикаторов развития отраслевых комплексов, стимулирующих инвестиционную активность.
Таким образом, модель оценки инвестиционной привлекательности отраслевых комплексов получает вид системы зависимостей, описывающих уровень и динамику экономического роста отраслевых комплексов, уровень и динамику доходности отраслевых комплексов, уровень и динамику риска отраслевых комплексов. Использование подобной системы зависимостей позволит всесторонне оценить уровень привлекательности отраслевых комплексов для потенциальных инвесторов [4].
Каждый из приведённых базовых векторов инвестиционной привлекательности отраслевых комплексов представляет собой интегральный показатель, исчисляемый на основе использования ряда частных параметров.
Проведённые эмпирические исследования дали возможность предложить ряд количественных индикаторов, позволяющих максимально точно интерпретировать экономический смысл категорий «экономический рост», «доходность» и «риск» применительно к отраслевым комплексам. Список данных индикаторов представлен в приведённой ниже таблице [4].
Таблица 1 – Список индикаторов, используемых в процессе моделирования инвестиционной привлекательности отраслевых комплексов
| Базовые векторы |
Индикаторы для оценки инвестиционной привлекательности отраслевых комплексов |
| Вектор экономического роста |
 – удельный вес отраслевого производства продукции в валовом внутреннем продукте (валовом региональном продукте) – удельный вес занятых в отрасли работников в общей численности занятого населения в стране (в регионе) – удельный вес объёма капитальных вложений в отрасль в совокупном объёме капитальных вложений в стране (в регионе) – удельный вес государственных капитальных вложений в совокупном объёме капитальных вложений в отрасль – удельный вес капитальных вложений, осуществляемых за счёт собственных финансовых ресурсов предприятий отрасли, в совокупном объёме капитальных вложений в отрасль – удельный вес объёма финансовых вложений предприятий отрасли в совокупном объёме финансовых вложений предприятий в стране (в регионе) – удельный вес собственного капитала предприятий отрасли в совокупном капитале предприятий отрасли (коэффициент автономии) |
| Вектор доходности |
 – коэффициент среднеотраслевой рентабельности активов – коэффициент среднеотраслевой рентабельности собственного капитала – коэффициент среднеотраслевой рентабельности продукции – коэффициент среднеотраслевой рентабельности текущих затрат |
| Вектор риска |
 – стандартное отклонение среднеотраслевой рентабельности активов – стандартное отклонение среднеотраслевой рентабельности собственного капитала – стандартное отклонение среднеотраслевой рентабельности продукции – стандартное отклонение среднеотраслевой рентабельности текущих затрат |
III этап. Кластеризация (ранжирование) отраслевых комплексов по степени их инвестиционной привлекательности, проводимая на основе анализа состояния отраслевых комплексов и тенденций их развития. Представление количественных оценок кластеризации отраслевых комплексов в качестве результирующего признака их инвестиционной привлекательности.
Для построения любой регрессионной зависимости необходимо определиться не только с характером независимых параметров формируемой модели, но и с характером результирующего признака.
С этой целью отраслевые комплексы, данные состояния и развития которых образуют базу данных, используемую для моделирования, подвергаются кластеризации по степени их привлекательности для потенциального инвестора. Поскольку модель оценки инвестиционной привлекательности отраслевых комплексов представляет собой систему зависимостей, то кластеризация отраслевых комплексов проводится отдельно по степени экономического роста, наблюдаемого в отраслевых комплексах, по степени их доходности и по степени их риска. Иными словами для каждой отдельной зависимости, описывающей одно из качеств инвестиционной привлекательности отраслевых комплексов, предусматривается отдельная кластеризация отраслевых комплексов на основе анализа специфического набора частных индикаторов. При этом в ходе кластеризации отраслевых комплексов учитываются следующие признаки:
- абсолютный уровень включаемых в модель параметров;
- поправка на динамику параметров модели.
Базовые критерии оценки параметров, составляющих формируемую модель, представлены в приведённых ниже таблицах [4].
Таблица 2 – Базовые критерии кластеризации отраслевых комплексов по параметрам вектора экономического роста
| Показатели |
Оценки параметров |
||||
|
крайне |
неудовлетворительно |
в районе |
удовле-творительно |
хорошо |
|
| 1. Удельный вес отраслевого производства продукции в валовом внутреннем продукте (валовом региональном продукте) (ER1) |
0-2,5% |
2,5-5,0% |
5,0-7,5% |
7,5-10,0% |
>10,0% |
| 2. Удельный вес занятых в отрасли работников в общей численности занятого населения в стране (в регионе) (ER2) |
0-2,5% |
2,5-5,0% |
5,0-7,5% |
7,5-10,0% |
>10,0% |
| 3. Удельный вес объёма капитальных вложений в отрасль в совокупном объёме капитальных вложений в стране (в регионе) (ER3) |
0-5,0% |
5,0-10,0% |
10,0-20,0% |
20,0-30,0% |
>30,0% |
| 4. Удельный вес государственных капитальных вложений в совокупном объёме капитальных вложений в отрасль (ER4) |
0-10,0% |
10,0-20,0% |
20,0-40,0% |
40,0-50,0% |
>50,0% |
| 5. Удельный вес капитальных вложений, осуществляемых за счёт собственных финансовых ресурсов предприятий отрасли, в совокупном объёме капитальных вложений в отрасль (ER5) |
0-20,0% |
20,0-40,0% |
40,0-60,0% |
60,0-80,0% |
>80,0% |
| 6. Удельный вес объёма финансовых вложений предприятий отрасли в совокупном объёме финансовых вложений предприятий в стране (в регионе) (ER6) |
0-5,0% |
5,0-10,0% |
10,0-15,0% |
15,0-20,0% |
>20,0% |
| 7. Удельный вес собственного капитала предприятий отрасли в совокупном капитале предприятий отрасли (коэффициент автономии) (ER7) |
0-5,0% |
5,0-10,0% |
10,0-20,0% |
20,0-50,0% |
>50,0% |
|
Оценки |
1 |
2 |
3 |
4 |
5 |
Таблица 3 – Базовые критерии кластеризации отраслевых комплексов по параметрам вектора доходности
| Показатели |
Оценки параметров |
||||
|
крайне |
неудовлетворительно |
в районе |
удовле-творительно |
хорошо |
|
| 1. Коэффициент среднеотраслевой рентабельности активов (D1) |
<-10,0% |
-10,0-0,0% |
0,0-5,0% |
5,0-15,0% |
>15,0% |
| 2. Коэффициент среднеотраслевой рентабельности собственного капитала (D2) |
<-30,0% |
-30,0-0,0% |
0,0-20,0% |
20,0-50,0% |
>50,0% |
| 3. Коэффициент среднеотраслевой рентабельности продукции (D3) |
<-20,0% |
-20,0-0,0% |
0,0-5,0% |
5,0-20,0% |
>20,0% |
| 4. Коэффициент среднеотраслевой рентабельности текущих затрат (D4) |
<-20,0% |
-20,0-0,0% |
0,0-5,0% |
5,0-20,0% |
>20,0% |
|
Оценки |
-2 |
-1 |
0 |
+1 |
+2 |
Таблица 4 – Базовые критерии кластеризации отраслевых комплексов по параметрам вектора риска
| Показатели |
Оценки параметров |
||||
|
хорошо |
удовле-творительно |
в районе |
неудовлетворительно |
крайне |
|
| 1. Стандартное отклонение (среднее квадратическое отклонение) среднеотраслевой рентабельности активов (R1) |
<0,025 |
0,025-0,050 |
0,050-0,075 |
0,075-0,100 |
>0,100 |
| 2. Стандартное отклонение (среднее квадратическое отклонение) среднеотраслевой рентабельности собственного капитала (R2) |
<0,15 |
0,15-0,30 |
0,30-0,45 |
0,45-0,60 |
>0,60 |
| 3. Стандартное отклонение (среднее квадратическое отклонение) среднеотраслевой рентабельности продукции (R3) |
<0,05 |
0,05-0,10 |
0,10-0,15 |
0,15-0,20 |
>0,20 |
| 4. Стандартное отклонение (среднее квадратическое отклонение) среднеотраслевой рентабельности текущих затрат (R4) |
<0,05 |
0,05-0,10 |
0,10-0,15 |
0,15-0,20 |
>0,20 |
|
Оценки |
+2 |
+1 |
0 |
-1 |
-2 |
Поправка на динамику используется по результатам оценки каждого из параметров за последние три года. В зависимости от характера этой динамики конечный уровень оценки корректируется в соответствии со следующими нормами:
- «крайне положительная» – +20%;
- «положительная» – +10%;
- «стабильная» – 0%;
- «отрицательная» – -10%;
- «крайне отрицательная» – -20%.
В целом, результирующий признак по каждой из зависимостей, составляющих модель оценки инвестиционной привлекательности отраслевых комплексов, представляет собой комплексный показатель, уровень которого определяется как сумма репрезентативных параметров, характеризующих различные аспекты состояния и тенденций развития отраслевых комплексов. В качестве репрезентативных параметров в данном случае рассматриваются количественные оценки кластеризации отраслевых комплексов по параметрам экономического роста, доходности и риска.
Следует отметить тот факт, что для адекватной оценки результирующего признака необходимо использовать обоснованный алгоритм расчёта, позволяющий представить этот индикатор в качестве интегрального показателя. В настоящее время для подобных целей используются следующие подходы [4,5]:
- свод численных значений факториальных параметров на основе их сложения (с учётом весовых нагрузок рассматриваемых параметров или без их учёта);
- свод численных значений факториальных параметров по формуле средней (с учётом весовых нагрузок рассматриваемых параметров или без их учёта);
- свод численных значений факториальных параметров по формуле многомерной средней (с учётом весовых нагрузок рассматриваемых параметров или без их учёта).
Поскольку для расчёта интегрального показателя результирующего признака используются количественные оценки кластеризации отраслевых комплексов по параметрам, то особой разницы в использовании того или иного подхода оценки интегрального результирующего признака не наблюдается.
Это обуславливается абсолютной унифицированностью размерности количественных оценок кластеризации и идентичностью количества и характера возможных кластерных групп по параметрам, формирующим модель оценки инвестиционной привлекательности отраслевых комплексов.
Таким образом, интегральный показатель результирующего признака определяется в виде суммы репрезентативных параметров без учёта факторных нагрузок последних. Отказ от взвешивания репрезентативных параметров обусловлен отсутствием научно обоснованных подходов учёта степени приоритетности отдельных параметров в их совокупности. Использование экспертных оценок для решения проблемы обоснованных факторных весовых нагрузок представляется неприемлемым, поскольку данный подход предполагает применение методов, ориентированных на личностные приоритеты экспертов. Использование экспертных оценок отнюдь не решает проблемы отсутствия факторных нагрузок, а скорее переводит её в плоскость проблемы достоверности экспертных оценок [4,5].
Приведённый алгоритм формализации результирующего признака лежит в основе расчёта интегральных индексов первого порядка, описывающих уровень экономического роста, уровень доходности и уровень риска, характерные для отдельной отрасли, а также в основе расчёта интегрального индекса инвестиционной привлекательности отраслевых комплексов, который сочетает в себе названные интегральные индексы первого порядка.
Если спроецировать интегральный показатель результирующего признака на вектор оценки инвестиционной привлекательности отраслевых комплексов и придать его интерпретации качественный характер, то степень привлекательности отраслевых комплексов для потенциальных инвесторов можно оценивать в соответствии с критериями представленной ниже таблицы. В этой связи данные критерии позволяют обосновать интервалы инвестиционной привлекательности отраслевых комплексов.
Таблица 5 – Базовые критерии кластеризации отраслевых комплексов по степени их инвестиционной привлекательности
| Показатели |
Оценки параметров |
||||
|
крайне |
неудовлетворительно |
в районе |
удовле-творительно |
хорошо |
|
| 1. Вектор экономического роста |
1 |
2 |
3 |
4 |
5 |
| 2. Вектор доходности |
-2 |
-1 |
0 |
+1 |
+2 |
| 3. Вектор риска |
-2 |
-1 |
0 |
+1 |
+2 |
|
Сводные оценки |
-3 |
0 |
3 |
6 |
9 |
|
Интервалы инвестиционной |
<-3 |
-3-0 |
0-6 |
6-9 |
>9 |
Однако использование данных интервалов для кластеризации отраслевых комплексов по степени их инвестиционной привлекательности представляется несколько грубым и неоднозначным подходом. Дело в том, что степень воздействия каждого из интегральных индексов первого порядка (векторов) на интегральный индекс инвестиционной привлекательности отраслевых комплексов имеет разнонаправленный характер, что может сказаться на точности расчёта конечного результирующего признака.
В связи с этим более обоснованным выглядит представление инвестиционной привлекательности отраслевых комплексов в виде их позиционирования в инвестиционном поле. Если последнее представить в виде трёхмерного графика, в качестве осей которого выступают вектор экономического роста, вектор доходности и вектор риска, то позиционирование отраслевых комплексов в инвестиционном поле получит высокую степень наглядности. Таким образом, конечное выражение инвестиционной привлекательности отраслевых комплексов получает графическую интерпретацию.
IV этап. Построение модели оценки инвестиционной привлекательности отраслевых комплексов.
На сегодняшний день большинство моделей оценки и прогнозирования финансовых и экономических преференций носят линейных характер. Однако для них характерен один весьма существенный недостаток – они не позволяют учесть разнонаправленность векторов динамики финансовых и экономических составляющих этих моделей. Поэтому при построении модели оценки инвестиционной привлекательности отраслевых комплексов были рассмотрены два альтернативных алгоритма моделирования [4]:
- формирование модели оценки индекса инвестиционной привлекательности отраслевых комплексов на основе использования алгоритма мультипликативного регрессионного анализа (линейный тип модели);
- формирование модели оценки индекса инвестиционной привлекательности отраслевых комплексов на основе использования регрессии экспоненциального типа (нелинейный тип модели).
Выбор регрессионной зависимости экспоненциального типа для формирования нелинейного типа модели обусловлен результатами эмпирических исследований, которые показали, что динамика индекса инвестиционной привлекательности отраслевых комплексов наиболее полно и наиболее точно описывается экспоненциальной зависимостью.
Общий вид формируемой модели представлен следующей системой зависимостей:
- для линейного типа модели оценки инвестиционной привлекательности отраслевых комплексов
|
|
 |
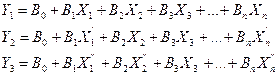(1) |
- для нелинейного типа модели оценки инвестиционной привлекательности отраслевых комплексов
|
|
 |
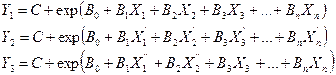(2) |
В ходе моделирования конечная модель была ориентирована на достижение максимальной достоверности ожидаемых результатов.
Далее в зависимости от типа формируемой модели используется соответствующий алгоритм моделирования индекса инвестиционной привлекательности отраслевых комплексов.
1. Алгоритм формирования модели оценки индекса инвестиционной привлекательности отраслевых комплексов на основе использования мультипликативного регрессионного анализа (линейный тип модели) [4,6].
Как правило, методом оценки, на основании которого производится поиск скрытой регрессионной зависимости, описывающей индекс инвестиционной привлекательности отраслевых комплексов, является метод наименьших квадратов.
В зависимости от характера интерпретации алгоритма метода наименьших квадратов для построения регрессионных зависимостей используются стандартный метод или пошаговый (включения и исключения) метод.
Стандартный метод моделирования состоит в использовании стандартных функций ограничений процесса моделирования.
Пошаговый метод предусматривает построение модели последовательно по шагам. Для пошагового метода включения на каждом шаге оценивается вклад в регрессионную функцию не включённых в модель переменных. Переменная, обеспечивающая наибольший вклад, включается в модель, после чего производится переход к следующему шагу. Для пошагового метода исключения характерно включение в модель на первом этапе всех переменных, после чего производится их последовательное исключение. Для пошаговых методов предусмотрена возможность использования нестандартных функций ограничений процесса моделирования. К их числу относятся:
- толерантность модели;
- значения статистики F для включения переменной в модель;
- значения статистики F для исключения переменной из модели;
- число шагов моделирования.
2. Алгоритм формирования модели оценки индекса инвестиционной привлекательности отраслевых комплексов на основе использования регрессии экспоненциального типа (нелинейный тип модели) [4,6].
В первую очередь выбирается метод оценки, на основании которого производится поиск скрытой экспоненциальной зависимости, описывающей индекс инвестиционной привлекательности отраслевых комплексов. В качестве такого метода оценки используется метод Квази-Ньютон. В случае если процесс оценки параметров вновь формируемой модели сошёлся, необходимо определить насколько оценённая модель подходит к данным, т.е. проверить степень её адекватности. Если же процесс оценки параметров вновь формируемой модели не сошёлся, необходимо выполнить следующие операции:
- изменить метод оценки параметров, т.е. провести оценку параметров симплекс методом, методом Розенброка или методом Хука-Джевиса;
- изменить вид вновь формируемой математической зависимости, т.е. придать ей вид линейной регрессии, кусочно-линейной регрессии, логистической регрессии или регрессии специфического (частного) характера.
Первичный анализ результатов моделирования заключается в оценки таких параметров как:
- точечные оценки параметров модели;
- стандартные ошибки оценки параметров модели;
- стандартизированные коэффициенты регрессионного уравнения;
- стандартные ошибки оценки стандартизированных коэффициентов регрессионного уравнения;
- t-критерий, который используется для проверки гипотезы о равенстве 0 свободного члена регрессии;
- уровень значимостиp, представляющий вероятность ошибки, связанной с распространением наблюдаемого результата на совокупную популяцию.
V этап. Проверка построенной модели на значимость и адекватность.
Гипотеза о незначимости регрессионной модели проверяется на основе использования дисперсионного анализа. Индикаторами оценки значимости модели и весовых факторных нагрузок её параметров являются статистика критерия Фишера F и уровень значимости p.
Линейная регрессионная зависимость называется адекватной, если предсказанные по ней значения переменной Y согласуются с результатами наблюдений. Грубая оценка адекватности модели может быть проведена непосредственно по графику остатков, которые представляют собой разницу между наблюдаемыми значениями и спрогнозированными с помощью модели. Если модель адекватна, то остатки ведут себя достаточно хаотично, в известном смысле напоминая белый шум, т.е. являются следствием случайных ошибок наблюдений, которые должны быть независимыми нормально распределёнными случайными величинами с нулевыми средними и равными дисперсиями. При этом в остатках не наблюдаются систематическая составляющая и резкие выбросы, в чередовании их знаков нет никаких закономерностей, остатки являются независимыми друг от друга. Всякое отклонение от названных условий отражается на поведении остатков.
График стандартизированных остатков позволяет обнаружить следующие дефекты регрессионной модели и исходных данных:
- наличие выбросов, т.е. таких остатков, которые по абсолютному значению значительно превосходят все прочие остатки;
- нарушение условия постоянства дисперсии ошибок для всех наблюдений; если все остатки укладываются в симметричную относительно нулевой линии полосу шириной
2S, то дисперсии ошибок наблюдений постоянны; - криволинейных характер графика остатков показывает, что в регрессионной модели не учтены факторы, оказывающие существенное влияние на зависимую переменную Y.
Далее проводится проверка гипотезы о нормальности распределения остатков. С этой целью остатки проецируются на нормальном вероятностном графике и на полунормальном вероятностном графике. Если наблюдается расположение точек близко к прямой, то можно предположить, что остатки распределены по нормальному закону. Гипотезу о нормальном распределении остатков можно также проверить по критерию 
или критерию Колмогорова-Смирнова.
Кроме того, при оценке значимости и адекватности вновь сформированной модели необходимо рассчитать ряд количественных критериев, описывающих характер корреляционной связи между результирующим признаком и независимыми переменными, а также показатели, характеризующие абсолютные потери при моделировании.
В качестве таких критериев выступают:
- коэффициент множественной корреляции – описывает степень линейной зависимости между результирующим признаком и независимыми переменными модели; в случае с простой линейной регрессией данный показатель равен модулю коэффициента корреляции;
- коэффициент детерминации, представляющий собой квадрат коэффициента множественной корреляции. Если регрессионная модель значима, то коэффициент детерминации равен той доле дисперсии ошибок наблюдений, которая объясняется регрессионной моделью;
- скорректированный коэффициент детерминации;
- стандартная ошибка наблюдений – характеризует стандартное отклонение выборочного среднего, рассчитанное по выборке из генеральной совокупности;
- суммарные потери;
- объяснённая дисперсия, которая характеризует долю вариации данных, учитываемых вновь созданной моделью.
Для оценки адекватности вновь формируемой модели особое внимание следует обратить на коэффициент детерминации, характеризующий долю общего разброса относительно выборочного среднего зависимой переменной, которая объясняется построенной регрессией. Чем меньше разброс значений остатков около линии регрессии по отношению к общему разбросу значений, тем лучше прогноз. Уровень коэффициента детерминации является индикатором степени подгонки модели к данным. Значение этого показателя варьирует в пределах от 0 до 1. Чем ближе его уровень к 1, тем лучше построенная зависимость объясняет разброс наблюдений. В известной степени данный показатель может рассматриваться в качестве критерия оценки предсказательной силы модели.
В соответствии с изложенной процедурой моделирования инвестиционной привлекательности отраслевых комплексов в рамках данного исследования подготовлены:
- модель оценки инвестиционной привлекательности отраслевых комплексов, сформированная на основе использования мультипликативного регрессионного анализа для периода глубиной 14 лет – 1995-2008 гг.
|
|
 |
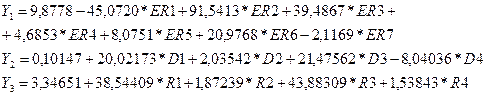(3) |
- модель оценки инвестиционной привлекательности отраслевых комплексов, сформированная на основе использования регрессии экспоненциального типа для периода глубиной 14 лет – 1995-2008 гг.
|
|
 |
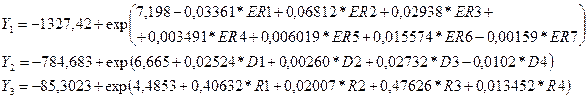(4) |
Тот факт, что указанные модели разработаны с использованием альтернативных способов моделирования, обеспечивает большую степень свободы в выборе эффективного инструментария оценки и прогнозирования индекса инвестиционной привлекательности отраслевых комплексов. Тем не менее, как модели, сформированные на основе использования алгоритма мультипликативного регрессионного анализа, так и модели, сформированные на основе использования регрессии экспоненциального типа, обеспечивают весьма высокую степень точности оценки уровня привлекательности объекта исследования для потенциальных инвесторов. Об этом свидетельствуют результаты статистического исследования как сформированных моделей, так и базы данных, составленной с целью выявления скрытых математических зависимостей, описывающих инвестиционную привлекательность отраслевых комплексов.
Следует отметить тот факт, что уровень предсказательной силы предлагаемых моделей, который описывается коэффициентом детерминации, очень высок. Как для моделей, сформированных на основе использования алгоритма мультипликативного регрессионного анализа, так и для моделей, сформированных на основе использования регрессии экспоненциального типа, уровень коэффициента детерминации варьирует в пределах от 0,92 до 0,95. Иными словами, построенные регрессионные зависимости объясняют 92-95% общего разброса относительно выборочного среднего зависимой переменной, что свидетельствует о хороших качественных характеристиках созданных моделей.
Анализ стандартизированных остатков, демонстрирующих дефекты вновь созданных моделей, позволяет утверждать, что эти остатки являются следствием случайных ошибок наблюдений, которые представляются независимыми нормально распределёнными случайными величинами. Следовательно, сформированные зависимости обладают должной степенью адекватности.
В силу этого можно констатировать, что отличительной чертой созданных моделей является весьма высокая точность прогноза инвестиционной привлекательности отраслевых комплексов в сочетании с очевидной простотой используемого для этой цели инструмента оценки.
Однако, поскольку инвестиционное поле России в последние годы подвержено постоянному воздействию множества политических, экономических, финансовых и социальных факторов, степень влияния которых на протекающие и ожидаемые инвестиционные процессы неоднозначна, при формировании прогноза индекса инвестиционной привлекательности отраслевых комплексов необходимо учитывать характер изменчивости инвестиционного поля и факторов, оказывающих на него влияние. Поэтому сформулированные модели следует использовать для построения краткосрочных или среднесрочных прогнозов инвестиционной привлекательности отраслевых комплексов, не превышающих по своей продолжительности, соответственно, одного года или трёх лет.
Кроме того, с течением времени наблюдается определённое изменение степени значимости параметров, составляющих модель оценки индекса инвестиционной привлекательности отраслевых комплексов. Отдельные параметры способны приобрести статус факторов, определяющих уровень рассчитываемого индекса, другие параметры, напротив, трансформируются в незначительные факторы, не оказывающие существенного влияния на уровень инвестиционной привлекательности отраслевых структур.
В силу названных причин следует проводить актуализацию сформулированных моделей оценки индекса инвестиционной привлекательности не реже одного раза в три года (при наличии возможности – не реже одного раза в год). Это позволит обеспечить учёт динамики значимости факторов, в той или иной степени определяющих уровень привлекательности отраслевых комплексов для потенциальных инвесторов, и, как следствие, повысить точность прогноза индекса инвестиционной привлекательности отраслей.
Наряду с оценкой количественного индекса инвестиционной привлекательности отраслевых комплексов выше говорилось о целесообразности графического представления позиций отдельного комплекса в инвестиционном поле. Если последнее представить в виде трёхмерного графика, в качестве осей которого выступают вектор экономического роста, вектор доходности и вектор риска, то позиционирование отраслевых комплексов в инвестиционном поле получит высокую степень наглядности. Тем самым, конечное выражение инвестиционной привлекательности отраслевых комплексов получает графическую интерпретацию.
На этих графиках весьма наглядно прослеживается характер изменения с течением времени степени значимости того либо иного вектора инвестиционного поля в свете воздействия, которое он оказывал на уровень инвестиционной привлекательности отраслевых комплексов.
Кроме того, использование подобного подхода позволяет весьма наглядно продемонстрировать степень предпочтения для потенциальных инвесторов тех либо иных отраслевых комплексов в сравнении между последними.
В целом, сформированный в рамках данного исследования комплексный инструментарий оценки и прогнозирования индекса инвестиционной привлекательности отраслевых комплексов отличается универсальностью и может быть использован на практике при исследовании инвестиционного поведения хозяйствующих субъектов и организации эффективного финансового и инвестиционного менеджмента.
Читайте также
Библиографический список
- Инвестиционное поведение российских предприятий / С. Дробышевский, А. Радыгин, И. Горшунов, О. Изряднова, А. Ильин, Г. Мальгинов, М. Турунцева, С. Цухло, И. Шкребела. – М., 2003.
- Бланк И.А. Основы финансового менеджмента. В 2-х т. – К.: Эльга-Н, Ника-Центр, 1999.
- Бланк И.А. Основы инвестиционного менеджмента. В 2-х т. – К.: Эльга-Н, Ника-Центр, 2001.
- Перцухов В.И., Панасейкина В.С. Моделирование инвестиционного поведения экономических систем. В 2-х т.: Монография. – Краснодар: Изд-во ООО «Ризограф», 2007.
- Перцухов В.И. Инвестиционная привлекательность организаций: методология оценки, прогнозирования и моделирования. В 3-х т.: Монография. – Краснодар: Изд-во ООО «Ризограф», 2008.
- Боровиков В.П. STATISTICA. Искусство анализа данных на компьютере: Для профессионалов. 2-е изд. (+CD). – СПб.: Питер, 2003.
References
- Investment behavior of Russian enterprises / S. Drobyshevsky Radygin A., I. Gorshunov, O. Izryadnova, Ilyin, G. Malginov, Turuntseva M., S. Tsukhlo, I. Shkrebela. – M., 2003.
- Blank I.A. Fundamentals of Financial Management. In 2 volumes – K.: Elga-N, Nick Center, 1999.
- Blank I.A. Fundamentals of Investment Management. In 2 volumes – K.: Elga-N, Nick Center, 2001.
- Pertsuhov V.I., V.S. Panaseykina Modeling investment behavior of economic systems. In 2 volumes: Monograph. – Krasnodar: Publishing House Ltd. “printing machine” in 2007.
- Pertsuhov V.I. Investment attractiveness of organizations: an assessment methodology, forecasting and simulation. In 3 vol: Monograph. – Krasnodar: Publishing House Ltd. “printing machine”, 2008.
- Borovikov V.P. STATISTICA. Art data analysis on the computer: For professionals. 2nd ed. (+ CD). – St.: Peter, 2003.
