Оценка чувствительности нейросетевого метода построения динамической модели банкротства к выявлению признаков развивающегося процесса кризиса корпорации
Evaluation of the sensitivity of neural network method for constructing the dynamic model of bankruptcy to identify signs of a developing process of the crisis of the Corporation
Авторы
Аннотация
Проводится апробация оригинального нейросетевого логистического динамического метода построения модели банкротств. Исследована сходимость итераций восстановления индикатора банкротства по неполным данным, которое составляет основное «ядро» предложенного метода, а также регуляризация модели на байесовском ансамбле нейросетей. Проведено сравнение с 22 известными моделями банкротств: MDA – моделями, logit-моделями, экспертными моделями, рейтинговыми моделями, регламентированной методикой Правительства РФ.
Ключевые слова
Динамический нейросетевой метод, модель развивающегося банкротства, сходимость, регуляризация, оценка чувствительности метода, прогноз банкротства, сравнение с известными методами.
Рекомендуемая ссылка
Горбатков Станислав Анатольевич,Касимова Лиана Ириковна,Фарваев Ирик Рафитович. Оценка чувствительности нейросетевого метода построения динамической модели банкротства к выявлению признаков развивающегося процесса кризиса корпорации // Современные технологии управления. ISSN 2226-9339. — №11 (59). Номер статьи: 5902. Дата публикации: 08.11.2015. Режим доступа: https://sovman.ru/article/5902/
Authors
Abstract
Pilot original neural network logistic dynamic method of building the model of bankruptcies. Investigated the convergence of the iterations of the restoration indicator bankruptcy on incomplete data, which makes the basic "core" of the proposed method and regularization model on Bayesian ensemble of neural networks. Compared with 22 known models of bankruptcies: MDA models, logit models, expert models, rating models, regulated by the method of the Government of the Russian Federation.
Keywords
Dynamic neural network method, the model of an evolving bankruptcy, convergence, regularization, evaluation of the sensitivity of the method, the prediction of bankruptcy, comparison with known methods.
Suggested citation
Gorbatkov Stanislav Anatol'evich,Kasimova Liana Irikovna,Farvaev Irik Rafitovich. Evaluation of the sensitivity of neural network method for constructing the dynamic model of bankruptcy to identify signs of a developing process of the crisis of the Corporation // Modern Management Technology. ISSN 2226-9339. — №11 (59). Art. # 5902. Date issued: 08.11.2015. Available at: https://sovman.ru/article/5902/
Введение
Вопрос об оценке изменяющегося во времени финансово-экономического состояния корпораций интересует многих: банки при выдаче кредитов и дальнейшем управлении процесса обслуживания кредитного портфеля; корпорации для обеспечения своей экономической безопасности; предпринимателей, заключающих сделки; финансовые структуры, организующие выпуск корпоративных облигаций и др. Поэтому вопросу диагностики банкротств корпораций посвящено большое число работ. К 2014 г. их число составило более двухсот [1].
Однако наиболее важный вопрос разработки динамических (прогнозных) моделей банкротств с непрерывным временем остается малоисследованным. Можно выделить две причины такой ситуации:
- Высокий уровень зашумленности данных, вплоть до их сознательного искажения, что вызывается, например, стремлением заемщиков банков показать с выгодной стороны свое финансово-экономическое состояние.
- Неполнота данных: в исследуемых в статье нейросетевых адаптивных моделях банкротства во временных срезах для обучения модели, необходима информация как по экзогенным переменным (входным факторам), так и по эндогенным выходным переменным – индикаторам банкротства. Как правило, метки «банкрот – набанкрот» для корпорации в выборке данных известны только после соответствующей юридической процедуры, т.е. для последнего временного среза
.
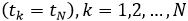В [2] авторами был предложен итерационный нейросетевой логистический динамический метод (НЛДМ) построения динамической модели банкротств с неполными данными, который практически компенсирует указанные выше две причины. При этом авторов, прежде всего, интересовал вопрос: насколько эффективно «сработают» идеи, заложенные в алгоритм НЛДМ. По вопросу метода обоснования адекватности предложенные модели и верификации в силу ограниченности объема статьи в [2] были сделаны лишь первые шаги. Поэтому в рассматриваемой работе первым посылом к исследованию была оценка устойчивости модели и, соответственно, ее регуляризация на байесовском ансамбле нейросетей. Вторым посылом, как и для любого предлагаемого метода, послужило стремление авторов к оценке качества НЛДМ путем его всестороннего сравнения с известными группами методов диагностики банкротств, включая современные продвинутые логистические методы [1].
1. Краткое описание алгоритма НЛДМ
Изложим в очень сжатой форме алгоритм НЛДМ с тем, чтобы выявить механизм восстановления динамических закономерностей, скрытых в данных, и оценить чувствительность модели по выходному показателю-вероятности риска банкротства 
.
Требуется построить логистическую динамическую нейросетевую модель оценки вероятности риска банкротства вида
(1)
где показатель экспоненты 
восстанавливается по неполным данным 
с помощью нейросетевого отображения вида [3]:
(2)
Здесь оператор нейросетевого отображения
(3)
где 
, 
– пространства действительных чисел размерности 
и 1 соответственно; 
– матрица параметров (синаптических весов) нейросети; 
– непрерывно изменяющееся время; 
– дискретное время для 
-го временного «среза» в данных; 
– количество факторов 
Отметим, что в динамической модели банкротства (1), (2), (3) вероятность трансформируется к логистической функции в правой части (1), где в качестве аргумента логистической функции, т.е. числовой меры риска наступления нежелательного события, выступает значение нелинейной нейросетевой функции (2).
Вся сложность исследуемой проблемы построения динамической модели банкротств вида (1) по неполным данным 
где 
– гипотетические полные данные, состояла в двух моментах:
1) получения адекватной нейросетевой аппроксимации (2), (3);
2) восстановления кортежей (строк таблицы данных)
(4)
для всех временных «срезов», кроме последнего.
В основу предложенного в [2] НЛДМ положено допущение, что оператор нейросетевого отображения 
в (2), (3), т.е. оператор аппроксимации данных, является сжимающим либо, по крайней мере, не растягивающим [4] по выбранной норме в , . Термин «сжимающий оператор» здесь понимается в следующем смысле. В выборке данных реальных объектов (4) аргумент 
нейросетевой функции (2), а, следовательно, и значение этой функции 
«плывут» во времени. Между срезами 
значения и 
неизвестны. Пусть построен некоторый итерационный алгоритм уточнения значений 
в кортежах (4). Мы вводим гипотезу, что ошибка в задании векторного аргумента и матрицы синаптических весов в ходе упомянутого итерационного процесса будет «сжиматься» (либо не растягиваться) оператором в (2), (3) в соответствующую ошибку для 
. После расчета в нейросетевой модели (2), (3) имеет место дополнительное сжатие ошибки расчета с помощью логистической функции (1), поскольку реальный максимальный диапазон изменения аргумента экспоненты (примерно 
отображается в отрезок [0;1], т.е. 7, 8 раза!
Вторая гипотеза, на которую мы опираемся, вытекает из теории нейросетей [3], которая состоит в том, что восстанавливаемая (аппроксимируемая) нейросетью зависимость 
по (2), (3) есть непрерывная функция своих аргументов. Это означает, что малым изменениям аргументов соответствует малые изменения функции.
Тогда можно предположить, что, если взять два соседних временных «среза» из данных 
и 
, то информация о «плывущей» во времени зависимости 
в «срезе» с номером может быть вычислена приближенно через значение аргумента 
, которое известно в этом срезе из данных. Другими словами, мы считаем, что зависимость 
, построенную нейросетью (2), (3) для последнего «среза» 
в какой-то мере, т.е. с определенной ошибкой 
«наследуется» в соседнем временном «срезе» . Для уменьшения ошибки 
в [2] строится внутренний итерационный процесс восстановления эндогенной переменной 
поочередно во всех временных «срезах» 
с использованием нейросетей (2), (3). Затем организуется процесс внешних итераций по индексу 
с переобучением нейросетей по восстановленным данным .
Критерий остановки внешних итераций принят по сходимости невязки вида:
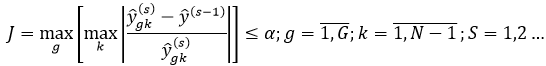(5)
где 
номер объекта в выборке; 
– малое число, например 
.
2. Квазибайесовский алгоритм регуляризации динамической модели банкротства
Поясним кратко суть процедуры регуляризации, основанной на парадигме сужения класса искомых решений обратной задачи восстановления зависимостей, скрытых в данных. В широко известной теории А.Н. Тихонова [4] решения обратных некорректных задач указанное «сужение» производится путем введения в алгоритм специального регуляризирующего (стабилизирующего) функционала А.Н. Тихонова, для построения которого, требуется использование некоторой априорной информации об искомом решении обратной задачи. Чаще всего – это информация о свойствах гладкости искомого решения. В данной статье используется та же парадигма «сужения», но другая концепция реализации этой парадигмы, основанная на байесовском подходе [2,5,6]. Идея состоит в том, что оператор нейросетевого отображения (2), (3) реализуется не на одной нейросети, а на байесовском ансамбле нейросетей, различающихся архитектурой, параметрами промежуточных слоев и видом активационных функций. После обучения ансамбля производится фильтрация априорных гипотез — нейросетевых моделей по критерию качества объяснения данных, например:
(6)
Здесь 
— количество точек тестового множества, где ошибка обобщения нейросети не превосходит заданного уровня 
:
(7)
В (6), (7) введены обозначения: 
– количество точек тестового множества, которое должно быть одинаковым для всех нейросетей, входящих в байесовский ансамбль; 
– номер нейросети в ансамбле; 
– число сетей в ансамбле; 
– частотный критерий приемлемого качества объяснения данных, задаваемый параметрами 
и , которые взаимосвязаны через прогностические свойства обученных нейросетей, т.е. 
, 
– некоторая непрерывная функция; 
— номер наблюдения в данных; звездочка сверху означает, что эта величина прошла операцию фильтрации в алгоритме (6), (7). Все расчетные выходные показатели далее усредняюся на отфильтрованном байесовском ансамбле нейросетей.
Механизм регуляризации нейросетевой модели согласно разработанному квазибайесовскому алгоритму заключаются в трех операциях:
1) Априорного задания архитектуры нейросетей в байесовском ансамбле и активационных функций в каждом скрытом слое сети. При этом, в модель вводится априорная информация, аккумулирующая профессиональный опыт исследователя и результаты предварительных вычислительных экспериментов. Естественно, это повышает прогностическую силу каждой нейросети в ансамбле.
2) Апостериорной фильтрации обученных и протестированных нейросетевых моделей (НСМ) по критерию качества (6), (7). Здесь за счет отсеивания НСМ, имеющих неприемлемое с точки зрения исследователя качество, сужается область искомых решений на байесовском ансамбле, что и является реализацией упомянутой выше парадигмы регуляризации согласно теории решения некорректных задач А.Н. Тихонова [4].
3) Усреднение расчетных моделируемых показателей на отфильтрованном байесовском ансамбле НСМ. Например, для критерия качества (6), (7):
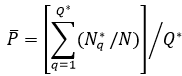(8)
где 
— число НСМ в отфильтрованном ансамбле. Регуляризирующая роль операции усреднения (8) очевидна: усреднение показателей на достаточно однородных элементах, всегда повышает устойчивость оценок, особенно в экономических задачах. В нашем случае однородность элементов 
, 
обеспечивается операцией фильтрации (6), (7), а также принадлежностью всех НСМ в ансамбле к единому классу моделей, т.е. «мета-гипотезе» 
[5,6].
3. Количественные оценки для алгоритма НЛДМ
В качестве исходных данных для построения динамической модели банкротств используется только выборка для множества объектов 
формируемая на основе стандартной бухгалтерской отчетности. В этом состоит удобство построения модели с точки зрения публичной доступности данных. По мнению авторов, модель (1) – (8) должна быть адаптирована для конкретной отрасли экономики (в нашем случае для одной из массовых отраслей – строительной). Использовалась международная база данных «Bereua Van Dijk» [7]. По методу из [7] была выбрана система из 16 показателей А.О. Недосекина [6,8], образующих четыре группы: I- рентабельности; II – ликвидности и платежеспособности; III – деловой активности; IV – финансовой устойчивости.
При выборе системы показателей из альтернативных традиционно сложившихся систем (в терминах описанного выше квазибайесовского алгоритма – это выбор на уровне мета-гипотезы) 
использовался критерий:
(9)
где 
— количество верно идентифицированных корпораций для данной зафиксированной байесовской метагипотезы 
– количество ошибок первого и второго рода соответственно при идентификации; 
— удельные веса показателей в (9), характеризующие их предпочтения, т.е. коэффициенты Фишберна [8]:
(10)
— количество ранжируемых показателей, входящих в критерий (9); – номер показателя. Формулу (10) можно использовать в случае, если множество показателей 
упорядочено в порядке убывания их предпочтения по значимости 
.
Затем была предпринята попытка для выбранной зафиксированной системы 16 показателей А.О. Недосекина [8] сократить число факторов по следующему простому алгоритму перебора. Вначале случайно выбрано по одному фактору из каждой группы I, II, III и IV и построены вспомогательные НСМ статические вида (2), где в число факторов не включалось время . Затем на каждом шаге итераций добавлялось по одному новому фактору, выбранному случайно из групп I, II, III и IV. После полного перебора факторов по индексу 
фиксировался тот оптимальный набор факторов 
, который соответствовал при тестировании модели условию:
(11)
где критерий 
– определялся по (9). Попытка оказалась успешной: удалось сократить число факторов в 2,29 раз, т.е. с 16 до 7 практически без ухудшения критерия качества (9). Были отобраны факторы из группы I – (рентабельности):
- R1 – общая рентабельность (балансовая прибыль/ (выручка от продаж + внереализационные доходы), %);
- R2- рентабельность активов (чистая прибыль / средняя балансовая стоимость активов, % за квартал);
- R3 — рентабельность собственного капитала ((чистая прибыль / капитал и резервы (за вычетом собственных акций, выкупленных у акционеров) – целевое финансирование и поступления + доходы будущих периодов, % за квартал);
Из группы II (ликвидности и платежеспособности):
- L1 – быстрый коэффициент ликвидности ((оборотные активы – запасы – налог на добавленную стоимость по приобретенным ценностям – долгосрочная дебиторская задолженность) / краткосрочные обязательства, не включая доходы будущих периодов), безразмерная величина);
- L2 – коэффициент покрытия запасов ((оборотные собственные средства + краткосрочные займы и кредиты + краткосрочная кредиторская задолженность) / средняя величина запасов, %).
Из группы III (деловой активности):
- А4 – оборачиваемость кредиторской задолженности (выручка от продажи без учета коммерческих и управленческих расходов / средняя кредиторская задолженность, за квартал);
Из группы IV (финансовой устойчивости):
- F1 – коэффициент финансовой зависимости (долгосрочные и краткосрочные обязательства (не включая доходы будущих периодов)/(капитал и резервы (за вычетом собственных акций, выкупленных у акционеров) – целевое финансирование и поступления + доходы будущих периодов, безразмерная величина).
Фрагмент результатов тестирования нейросетевой динамической модели для выборки [7] из 136 предприятий показан в
таблицах 1 и 2.
Результат оценок: практически процесс внешних итераций (по индексу 
) сошелся за два шага, причем все сети (кроме №10) показали один и тот же результат. При этом ошибки идентификации наблюдаются в одних и тех же точках тестового множества. Этот результат можно объяснить тем, что при переходе к следующей итерации (от к 
) нейросетевое отображение как указывалось выше, «сжимает» невязку для , т.е. отображение (2), (3) является сжимающим [4]. Дополнительное «сжатие» реализует также логистическая функция (1).
Усредненная на отфильтрованном ансамбле по (7) относительная погрешность 
расчета в НСМ, также уменьшилась примерно в 2,5 раза.
Полученная динамическая модель с непрерывным временем позволяет достаточно точно отслеживать характерную динамику вероятности банкротства и кредиторам, своевременно принимать соответствующие управляющие воздействия для реструктуризации задолженности.
Далее, построенной и апробированной оригинальной динамической нейросетевой модели банкротств предъявлялись для прогнозирования вероятности риска банкротства все восемь строительных корпораций из Таблицы 3. Для иллюстрации проведенных расчетов на Рисунках 1-8 приведены графики динамики вероятности банкротств этих корпораций.
Таблица 1. Результаты тестирования байесовского ансамбля динамических нейросетевых моделей для первого шага внешних итераций (S=1)
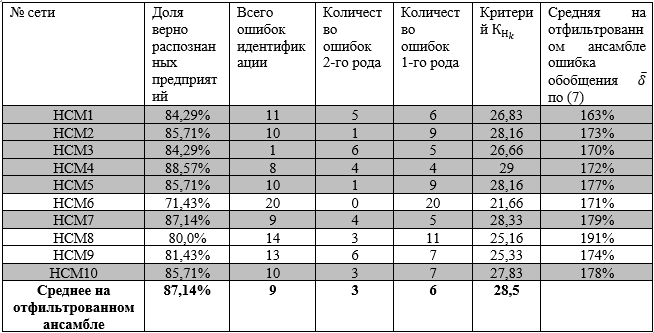
Таблица 2. Результаты тестирования динамического байесовского ансамбля нейросетей, для второго шага внешних итераций (S=2)
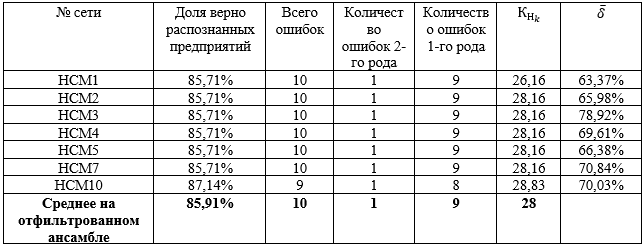
Таблица 3. Сводная таблица результатов расчета по известным моделям с использованием программы QFinAnalysis [9]
| Методы анализа финансового состояния предприятия |
ОАО «Главстрой Девелопмент» |
ОАО «Группа Компаний ПИК» |
ЗАО «Желдор- Ипотека» |
ОАО «Казань- Центрстрой» |
| MDA — модели | ||||
| Двухфакторная модель Альтмана | меньше 50% | меньше 50% | меньше 50% | меньше 50% |
| Двухфакторная модель Федотовой | очень высокая | очень высокая | очень высокая | очень высокая |
| Пятифакторная модель Альтмана | несостоятельно | несостоятельно | несостоятельно | несостоятельно |
| Пятифакторная модель Альтмана модифицированная |
несостоятельно | несостоятельно | несостоятельно | несостоятельно |
| Четырехфакторная модель Таффлера |
неопределено | неопределено | неопределено | неопределено |
| Четырехфакторная модель Лиса | малая | малая | малая | малая |
| Четырехфакторная модель Лиса скорректированная |
малая | малая | малая | малая |
| Четырехфакторная модель Спрингейта |
низкая | низкая | низкая | низкая |
| Четырехфакторная модель ИГЭА | 90-100% | 90-100% | 90-100% | 90-100% |
| Модель Сайфулина-Кадыкова | низкая | низкая | низкая | низкая |
| Модель Пареной-Долголаева | средняя | средняя | средняя | средняя |
| Модель Республики Беларусь | небольшой риск | небольшой риск | небольшой риск | небольшой риск |
| Модель Савицкой | финансово устойчиво | финансово устойчиво | финансово устойчиво | финансово устойчиво |
| logit-модели | ||||
| Модель Альтмана-Сабато | 100% | 98% | 98% | 0% |
| Модель Лина-Пьессе | 45% | 45% | 45% | 45% |
| Модель ДжуХа-Техонга | 50% | 48% | 48% | 38% |
| Модель Грузчинского | 1% | 1% | 1% | 1% |
| Модель Жданова | 1% | 1% | 1% | 1% |
| Экспертные модели | ||||
| Модель Зайцевой | высокая | высокая | высокая | высокая |
| Рейтинговые модели | ||||
| Модель КГТУ | 3 | 3 | 3 | 3 |
| Модель Бивера | 2 | 2 | 2 | 2 |
| Регламентированная методика | ||||
| Модель Правительства РФ 1994 г. | Б | Б | Б | Б |
| Расчет чистых активов | ||||
| Выполнение условия (ЧА>УК) | + | + | + | + |
| MDA — модели | ||||
| Двухфакторная модель Альтмана | меньше 50% | меньше 50% | меньше 50% | меньше 50% |
| Двухфакторная модель Федотовой | очень высокая | очень высокая | очень высокая | очень высокая |
| Пятифакторная модель Альтмана | несостоятельно | несостоятельно | несостоятельно | несостоятельно |
| Пятифакторная модель Альтмана модифицированная |
несостоятельно | несостоятельно | несостоятельно | несостоятельно |
| Четырехфакторная модель Таффлера |
неопределено | неопределено | неопределено | неопределено |
| Четырех факторная модель Лиса | малая | малая | малая | малая |
| Четырех факторная модель Лиса скорректированная |
малая | малая | малая | малая |
| Четырехфакторная модель Спрингейта |
низкая | низкая | низкая | низкая |
| Четырех факторная модель ИГЭА | 90-100% | 90-100% | 90-100% | 90-100% |
| Модель Сайфулина-Кадыкова | низкая | низкая | низкая | низкая |
| Модель Пареной-Долголаева | средняя | средняя | средняя | средняя |
| Модель Республики Беларусь | небольшой риск | небольшой риск | небольшой риск | небольшой риск |
| Модель Савицкой | финансово устойчиво | финансово устойчиво | финансово устойчиво | финансово устойчиво |
| logit-модели | ||||
| Модель Альтмана-Сабато | 0% | 98% | 0% | 97% |
| Модель Лина-Пьессе | 45% | 45% | 45% | 45% |
| Модель ДжуХа-Техонга | 48% | 48% | 8% | 46% |
| Модель Грузчинского | 1% | 1% | 1% | 1% |
| Модель Жданова | 1% | 1% | 1% | 1% |
| Экспертные модели | ||||
| Модель Зайцевой | высокая | высокая | высокая | высокая |
| Рейтинговые модели | ||||
| Модель КГТУ | 3 | 3 | 3 | 3 |
| Модель Бивера | 2 | 2 | 2 | 2 |
| Регламентированная методика | ||||
| Модель Правительства РФ 1994 г. | Б | Б | Б | Б |
| Расчет чистых активов | ||||
| Выполнение условия (ЧА>УК) | + | + | + | + |
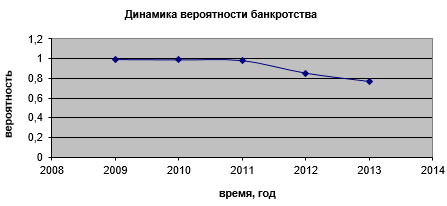
Рисунок 1. Динамика вероятности банкротства ОАО «Главстрой Девелопмент»
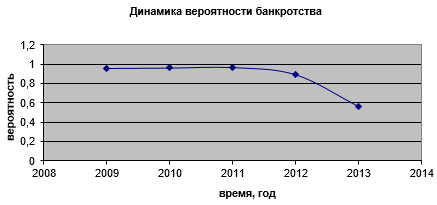
Рисунок 2. Динамика вероятности банкротства ЗАО «Желдорипотека»
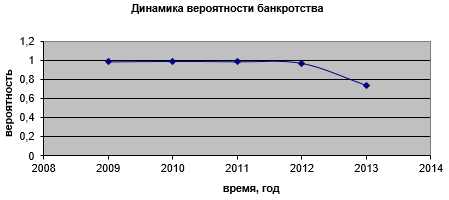
Рисунок 3. Динамика вероятности банкротства ОАО «Казаньцентрстрой»
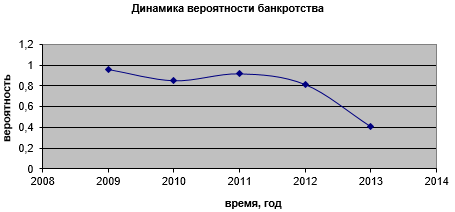
Рисунок 4. Динамика вероятности банкротства ОАО «ГК ПИК»
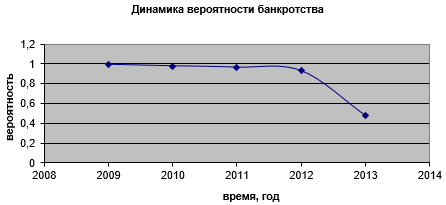
Рисунок 5. Динамика вероятности банкротства ОАО «Пензастрой»
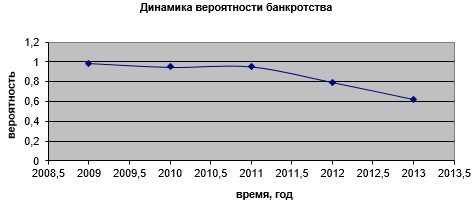
Рисунок 6. Динамика вероятности банкротства ОАО «Первый РС Трест»
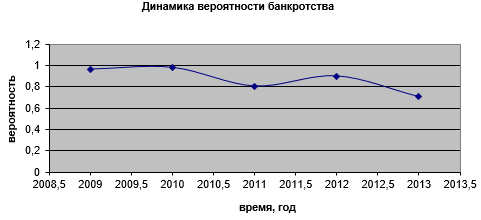
Рисунок 7. Динамика вероятности банкротства ОАО «Тюменская домостроительная компания»
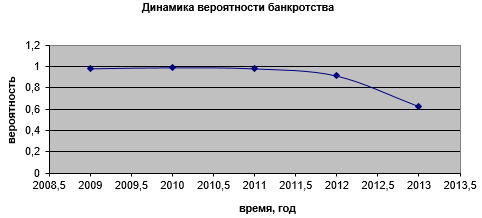
Рисунок 8. Динамика вероятности банкротства ОАО «Южно-Уральская Корпорация жилищного строительства и ипотеки»
По Рис. 1-8 и таблице 3 можно делать два важных вывода:
1) Наиболее положительную динамику выхода из банкротства имеет ОАО «Группа компаний ПИК».
2) Разработанная нейросетевая динамическая модель банкротств обладает достаточной чувствительностью в том аспекте, что изменение 7 факторов, введенных в модель, во времени 
отображаются в динамические функции вероятности риска банкротства по (1). Для различных предприятий из Рис. 1-8 кривые существенно различаются. В 2009 г. все 8 корпораций находились примерно в одинаковых условиях – они были близки к банкротству 
. Однако затем антикризисные меры действовали по-разному на развитие кризиса. Предприятие ОАО «ГК ПИК» и ОАО «Пензастрой» практически выбирались из кризиса (к 2013 вероятность риска банкротства снизилась до уровня 
), а у остальных корпораций эта вероятность была существенно выше 
, т.е. в этих предприятиях принятые антикризисные меры оказались недостаточными. При этом банки должны были своевременно позаботиться о реструктуризации задолженности этих предприятий, а предприятия – найти дополнительные источники финансирования, например, выпустить корпоративные облигации.
3. Сравнительный анализ НЛДМ с известными моделями банкротств по чувствительности к признаками банкротства
Сравнение НЛДМ по чувствительности к обнаружению стадий развивающегося процесса банкротства проводился для тех же 8 строительных корпораций, динамика состояния которых отображена на Рис. 1-8. Для сравнения использовались 22 известные модели банкротств из групп (Табл.3):
- линейные модели типа множественного дискриминантного анализа (MDA) [1];
- современные «продвинутые» logit-модели [1];
- экспертные модели [9];
- рейтинговые модели [9];
- регламентированная методика Правительства РФ [9].
Все эти модели и методики охвачены программным продуктом QfinAnalysis (версия 1.9) среде Excel разработанным В.Ю. Ждановым и И.Ю. Ждановым в Московском авиационном университете [9]. Исходными данными служила та же стандартная бухгалтерская отчетность, что и для формирования показателей R1, R2, R3, L1, L2, A4, F1, используемых в исследуемом нейросетевом логистическом динамическом методе (НЛДМ) по алгоритму (1) – (11). Результаты оценок показаны в таблице 3, где вероятность риска банкротства указана в %, либо в виде качественного показателя. В регламентированной методике Правительства РФ буква «Б» означает, что у предприятия присутствуют признаки банкротства. В рейтинговой модели КГТУ классы 1, 2, 3 образуют рейтинговые группы в порядке ухудшения финансово-экономических показателей, т.е. приближения к банкротству (таблица 4).
Таблица 4. Модель Казанского государственного технического университета (КГТУ)
- первый класс(1) – хорошее финансовое состояние (финансовые показатели выше среднеотраслевых, минимальный риск невозврата);
- второй класс (2) – удовлетворительное финансовое состояние (показатели на уровне среднеотраслевых, нормальный риск невозврата);
- третий класс (3) – неудовлетворительное финансовое состояние (показатели на уровне ниже среднеотраслевых, повышенный риск невозврата).
В рейтинговой модели Бивера аналогичный рейтинговый ряд классов 1, 2, 3 используется несколько другие показатели (см. Таблицу 5 ).
Таблица 5. Рейтинговая модель Бивера
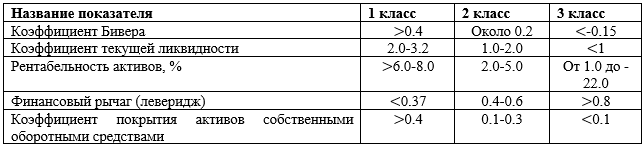
В последней строке таблицы 3 обозначено: ЧА – чистые активы; УК – уставный капитал. Знак «+» означает выполнение условия ЧАУК, знак «» означает невыполнение этого неравенства.
Результаты оценок. Если зафиксировать корпорацию, т.е. колонки таблицы 3, то все методы и регламентированная методика Правительства РФ 1994 г. дают существенно разноречивые результаты, которые не позволяют разработать эффективные практические рекомендации по реструктуризации кредиторской задолженности.
Если же зафиксировать строки таблицы 3, то все корпорации оцениваются одинаково в смысле близости к банкротству, т.е. зафиксированная модель их не различает. Исключением является модель Альтмана-Сабато, которая выделила два предприятия (ОАО «Казаньцентрстрой» и ОАО «Пензастрой») как далекие от банкротства.
Таким образом, 21 модель из 22 не обладают достаточной чувствительностью к признакам и стадиям развивающегося процесса кризиса на предприятиях. С другой стороны, оригинальный НЛДМ из [2], как было показано выше на Рис. 1-8 , обладает требуемой чувствительностью в динамике, т.е. дифференцирует предприятия по стадиям наблюдаемой в данный момент времени стадии банкротства, и, главное, метод позволяет сделать прогноз для заданного временного горизонта 
.
Общие выводы:
1. Для оригинального нейросетевого логистического динамического метода (НЛДМ) построения модели оценки риска банкротства с учетом непрерывного времени , который восстанавливает неполные данные во временных «срезах», проведена всесторонняя верификация чувствительности метода к выявлению признаков и стадий развивающегося кризиса корпораций.
2. Путем сравнения с оценками по 22 известным методам, включая современные «продвинутые» логистические методы, показано, что НЛДМ обладает достаточной контрастностью, т.е. способен дифференцировать характер динамических зависимостей 
вероятности риска банкротства. Для различных корпораций это позволяет кредитору отслеживать динамику при обслуживании кредитного портфеля и своевременно начать процедуры реструктуризации задолженности. Упомянутые 22 метода и методики, которые в основном охватывают современный арсенал моделей риска банкротства, таким свойством контрастности оценок не обладает. Следовательно, НЛДМ расширяет возможности современных экономико-математических инструментариев и, главное, позволяет более эффективно решать прикладные задачи финансового менеджмента.
3. Направление дальнейших исследований авторы видят в исследовании подобной прогнозной модели банкротств для другой массовой отрасли экономики – торговых предприятий.
Читайте также
Библиографический список
- Макеева Е.Ю., Горбатков С.А., Белолипцев И.И. О моделях диагностики банкротств организаций // Менеджмент и Бизнес – Администрирование. -2014. – №1. – С. 151-171.
- Полупанов Д.В., Горбатков С.А., Саетова Г. Д., Касимова Л.И. Исследование скорости сходимости итерационного нейросетевого динамического метода оценки риска банкротства // Математические методы и модели в исследовании государственных и финансовых рынков: Сборник материалов Всероссийской молодежной научно – практической конференции (27-28 апреля 2015 г., г. Уфа). В 3-х частях. Ч. II. / Отв. ред. И.У. Зулькарная. – Уфа: Аэтерна. – 2015. – с. 142-146.
- Галушкин А. И. Теория нейронных сетей. Кн. 1: Учебн. пособие для вузов. – М.: ИПРЖ, 2000. – 416 с.
- Тихонов А. Н., Арсенин В. Я. Методы решения некорректных задач: Монография /Изд. 2-е. — М.: Наука. Главная редакция физико-математической литературы, 1979. – 286 с.
- Шумский С.А. Байесова регуляризация обучения // Лекции для школы – семинара «Современные проблемы нейроинформатики» (23-25 января 2002 г.). – М.: МИФИ, 2002 (file://НейроОКИнтелсофт.htm)-33 с.
- Горбатков С. А., Полупанов Д. В., Макеева Е. Ю., Бирюков А. Н. Методологические основы разработки нейросетевых моделей экономических объектов в условиях неопределенности: Монография / Под ред. д.т.н., профессора Горбаткова С. А. – М.: Издательский дом «Экономическая газета», 2012. – 494 с.
- Горбатков С. А., Белолипцев И. И., Макеева Е. Ю. Выбор системы экономических показателей для диагностики и прогнозирования банкротств на основе байесовского подхода и интеллектуальных информационных технологий // Вестник Финансового Университета при Правительстве РФ. – 2013. — №4(76). – С. 50-62.
- Недосекин А.О. Методологические основы моделирования финансовой деятельности с использованием нечетко-множественных описаний. – Дисс. на соиск. ученой степени доктора экон. наук. – СПб: Санкт-Петербургский госуд. университет экономики и финансов, 2003. – 280 с.
- Жданов В,Ю., Жданов И.Ю., QFinAnalysis. Версия 1.9: [Электронный ресурс] // Школа финансового анализа [Официальный сайт]. URL: //www. beintrend.ru/qfinanalysisfree,2011
References
- Makeeva E.YU., Gorbatkov S.A., Belolipcev I.I. Models of diagnostic bankruptcies organizations [O modelyah diagnostiki bankrotstv organizacij]. Management and Business Administration. 2014. №1. pp. 151-171.
- Polupanov D.V., Gorbatkov S.A., Saetova G. D., Kasimova L.I. A study of the convergence rate of the iterative dynamic neural network risk assessment method bankruptcy [Issledovanie skorosti shodimosti iteracionnogo nejrosetevogo dinamicheskogo metoda ocenki riska bankrotstva]. Mathematical methods and models in the study of public and financial markets: Proceedings of the All-Russian Youth Scientific Practical Conference (April 27-28, 2015 in Ufa). In 3 parts. Part II. Ufa Aeterna. 2015. pp. 142-146.
- Galushkin A. I. The theory of neural networks [Teorija nejronnyh setej]. Bk. 1 Proc. manual for schools. M . IPRZH, 2000. 416 p.
- Tihonov A. N., Arsenin V. Ja. Methods of solving ill-posed problems, monograph [Metody reshenija nekorrektnyh zadach. Monografija]. Ed. 2nd. M . Nauka. Home edition of Physical and mathematical literature, 1979. 286 p.
- Shumskij S.A. Bayesian regularization training [Bajesova reguljarizacija obuchenija]. Lectures for school seminar Modern problems of neuroinformatics (23-25 January 2002). M. MiFi 2002 (file: //NeyroOKIntelsoft.htm) p. 33.
- Gorbatkov S. A., Polupanov D. V., Makeeva E. Ju., Birjukov A. N. The methodological basis for the development of neural network models of economic facilities in the face of uncertainty, monograph [Metodologicheskie osnovy razrabotki nejrosetevyh modelej jekonomicheskih ob#ektov v uslovijah neopredelennosti. Monografija]. M . Publishing house Economic newspaper, 2012. 494 p.
- Gorbatkov S. A., Belolipcev I. I., Makeeva E. Ju. The choice of economic indicators for the diagnosis and prediction of failures based on the Bayesian approach and intelligent information technologies [Vybor sistemy jekonomicheskih pokazatelej dlja diagnostiki i prognozirovanija bankrotstv na osnove bajesovskogo podhoda i intellektual’nyh informacionnyh tehnologij ]. Bulletin of the Financial University under the Government of the Russian Federation. 2013. №4 (76). pp. 50-62.
- Nedosekin A.O. Methodological bases of modeling of financial activity using fuzzy-multiple descriptions [Metodologicheskie osnovy modelirovanija finansovoj dejatel’nosti s ispol’zovaniem nechetko-mnozhestvennyh opisanij]. Diss. on soisk. a scientific degree of the doctor ehkon. Sciences. St. Petersburg. St. Petersburg gov’t. University of Economics and Finance, 2003. 280 p.
- Zhdanov V,Ju., Zhdanov I.Ju., QFinAnalysis. Version 1.9 [QFinAnalysis. Versija 1.9]. School Financial Analysis [Official site]. URL: // www. beintrend.ru/qfinanalysisfree,2011
