Метод комплексной пропорциональной оценки при формировании инвестиционного портфеля
Investment project selection by applying copras method
Авторы
Аннотация
Статья рассматривает особенности метода комплексной пропорциональной оценки при формировании инвестиционного портфеля, а также представляет его расширение, позволяющее учесть компоненту неопределенности среды в процессе реализации проекта.
Ключевые слова
инвестиционный проект, инвестиционный анализ, метод комплексной пропорциональной оценки.
Рекомендуемая ссылка
Сколота Денис Вадимович. Метод комплексной пропорциональной оценки при формировании инвестиционного портфеля // Современные технологии управления. ISSN 2226-9339. — №3 (39). Номер статьи: 3905. Дата публикации: 08.03.2014. Режим доступа: https://sovman.ru/article/3905/
Authors
Abstract
This paper examines the key features of complex proportional assessment method (COPRAS) for construction of investment portfolio, and also presents its extension.
Keywords
investment project, investment analysis, complex proportional assessment.
Suggested citation
Skolota Denis Vadimovich. Investment project selection by applying copras method // Modern Management Technology. ISSN 2226-9339. — №3 (39). Art. # 3905. Date issued: 08.03.2014. Available at: https://sovman.ru/article/3905/
Формирование инвестиционного портфеля – чрезвычайно сложная задача для любого руководителя, ответственного за принятие данного решения. В общем случае, руководитель принимает инвестиционное решение на основе совокупности критериев и их приоритетности как для него, так и для компании. Исходя из этого, процесс инвестиционного отбора может быть представлен в виде многокритериальной задачи принятия решений (МКПР).
Классические методы МКПР основаны на использовании исключительно точных данных о проектах, представляемых в виде дискретных значений. Однако, в реальном мире в рамках реализации проектов присутствует компонента неопределенности, не позволяющая нам получить абсолютно достоверные данные на этапе инвестиционного планирования. По этой причине, для решения задач реального мира применяют расширения классических методов МКПР.
Одним из методов МКПР является метод комплексной пропорциональной оценки проектов (COPRAS). Методы COPRAS-G и COPRAS-F являются расширениями классического варианта и имеют дело: в первом случае с интервалами данных, а во втором с нечетким множеством данных.
Однако, проблемы реального мира проект-менеджмента не всегда можно четко распределить по категориям в зависимости от точности получаемых данных. В реальности, использование методов МКПР требует одновременного использования нескольких типов данных в совокупности. В рамках данной статьи будет рассмотрена возможность использования смешанной формы метода комплексной пропорциональной оценки.
Метод комплексной пропорциональной оценки был представлен в 1994 году [1]. Особенностью данного метода является тот факт, что он позволяет учитывать как критерии максимизации, так и критерии минимизации.
Общая форма метода комплексной пропорциональной оценки (COPRAS)
Ранжирование альтернатив с помощью метода комплексной пропорциональной оценки предполагает прямую и пропорциональную зависимость значимости и приоритетности исследуемых альтернатив с системой критериев. Определение значимости и приоритетности альтернатив на основе данного метода может быть представлена в виде четырех шагов:
Шаг 1: Построение матрицы нормализованных значений. В процессе МКПР критерии зачастую представлены в различных единицах измерения. Для приведения критериев к сравнимым безразмерным величинам используется процедура нормализации [2,3]. Для нормализации в данном методе используется следующая формула:
![]() ,
,
где ![]() – нормализованное значение; xij – показатель проекта i относительно критерия j; m – количество альтернатив.
– нормализованное значение; xij – показатель проекта i относительно критерия j; m – количество альтернатив.
Шаг 2: Суммирование взвешенных нормализованных значений критериев по i-ой альтернативе.
В рассматриваемом методе каждая альтернатива может быть представлена в виде сумм критериев максимизации (S+i) и критериев минимизации (S-i):
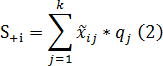
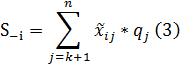
В формуле 2 и 3, k – число критериев максимизации, n – общее количество критериев и qi – значимость j-го критерия.
Шаг 3: Определение относительного веса каждой альтернативы. Относительный вес (Qi) i-ой альтернативы определяется следующим образом:
![]()
Шаг 4: Определение приоритетности альтернатив. Приоритетный порядок сравниваемых альтернатив определяется на основе их относительного веса.
Представленная процедура принятия решения может быть использована для оценки альтернатив и отбора наилучшей из них в случае, когда проект реализуется в абсолютно определенной среде с абсолютно предсказуемыми процессами [4].
Расширенная форма метода комплексной пропорциональной оценки (COPRAS—G)
Данный подход к оценке определяет значения критериев в виде интервала. Замена дискретного значения критерия на интервал значений требует определенного уровня модификации в системе ранжирования. В частности это касается шагов под номерами 1 и 2.
Шаг 1: Построение матрицы нормализованных значений.
![]()
![]() (6)
(6)
В формуле 5 и 6 числитель дроби есть нижняя и верхняя границы интервала значений по i-альтернативе относительно j-го критерия. В свою очередь результаты дробей представляют собой нормализованные значения границ интервала. [3]
Шаг 2: Суммирование взвешенных нормализованных значений критериев по i-ой альтернативе осуществляется следующим образом:
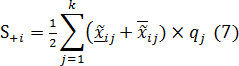
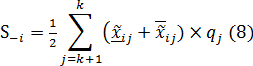
Процедура ранжирования альтернатив посредством расширенного метода комплексной пропорциональной оценки
В данном разделе мы рассмотрим процедуру отбора наиболее предпочтительных альтернатив при условии, что значения критериев представлены как в виде дискретных величин, так и в виде интервала. Данная процедура может быть представлены в форме последовательности из 8 шагов:
Шаг 1: Формирование перечня критериев для оценки инвестиционных альтернатив, первичный анализ.
Шаг 2: Формирование матрицы принятия решений.
Шаг 3: Нормализация матрицы принятия решений.
Шаг 4: Определение весов критериев.
Шаг 5: Калькуляция сумм максимизирущих критериев для каждой альтернативы.
Шаг 6: Калькуляция сумм минимизирующих критериев для каждой альтернативы.
Шаг 7: Калькуляция относительного веса каждой альтернативы, Qi.
Шаг 8: Ранжирование альтернатив и определение наилучшей из них.
Практический пример
Предположим, что необходимо отобрать наилучшую альтернативу среди четырех предложенных вариантов. Инвестор ставит перед проектом следующие цели [5]:
- Максимизация прибыли;
- Максимизация отдачи на первоначальные инвестиции;
- Минимизация срока окупаемости первоначальных инвестиций;
- Минимизация рисковой компоненты.
Для определения соответствия проекта требованиям будем использовать следующие финансовые критерии эффективности реализации проекта:
- Чистая приведенная стоимость (NPV) – для определение объема проектных поступлений;
- Индекс прибыльности (PI) – для определения уровня отдачи на первоначальные инвестиции;
- Срок окупаемости проекта (PBP) – для определения требуемого промежутка времени для выхода проекта на уровень окупаемости.
Любой инвестиционный проект несет в себе совокупность рисков. Определенная степень оценки рисковой составляющей может быть достигнута сочетанием двух индикаторов: внутренней нормы доходности (IRR) и срока окупаемости (PBP). Так например, проект с меньшим PBP и большим значением IRR менее рискованным и наоборот.
На основе вышеизложенного сформирована группа критериев, которая будет использована для оценки инвестиционных проектов: NPV, IRR, PI, PBP и Риск (R). Первые три критерия – максимизирующие, в то время как последующие два – минимизирующие. Также стоит отметить, что значения критериев NPV и PI представлены в виде интервалов.
Исходные данные проектов представлены в таблице 1.
Таблица 1: Исходные данные
| Проект |
Объем первоначальных инвестиций |
Ожидаемый ежегодный денежный поток |
Продолжительность проекта (год) |
|
CF0 |
CF |
T |
|
| Проект A |
140,00 |
35,00 |
7,00 |
| Проект B |
200,00 |
50,00 |
6,00 |
| Проект C |
170,00 |
40,00 |
8,00 |
| Проект D |
250,00 |
50,00 |
10,00 |
Предположим, что ставка дисконтирования для всех проектов равна 5%. Принимая во внимания сложность прогнозирования годовой ставки инфляции установим интервал ее движения от 2.5 до 5.5 %. Критерий R будет выражен в виде оценки по шкале от 0 до 10 в зависимости от уровня рисковой компоненты в рассматриваемых вариантах, где 0 – полное отсутствие риска и 10 – экстремально высокий уровень риска. Шкала представлена в таблице 2.
Таблица 2: Шкала уровней проектного риска
| Характеристика |
Оценка по шкале от 0 до 10 |
| Риск отсутствует |
0 |
| Чрезвычайно низкий уровень риска |
1 |
| Незначительный уровень риска |
3 |
| Средний уровень риска |
5 |
| Значительный уровень риска |
7 |
| Очень высокий уровень риска |
9 |
| Чрезвычайно высокий уровень риска |
10 |
Первоначальная матрица принятия решений представлена в таблице 3. Поскольку величины выражены в различных единицах измерения проводим процедуру нормализации, результаты которой представлены в таблице 4.
Таблица 3: Первичная матрица принятия решений
| Критерий |
NPV |
IRR |
PI |
PBP |
Risk |
||
|
Руб. |
% |
% |
Год |
||||
|
К1 |
К2 |
К3 |
К4 |
К5 |
|||
|
Вес критерия, qi |
0,45 |
0,21 |
0,11 |
0,12 |
0,11 |
||
|
Проект |
Нижний |
Верхний |
Нижний |
Верхний |
|||
|
A |
27,63 |
45,38 |
16,33% |
1,20 |
1,32 |
4 |
3 |
|
B |
14,61 |
34,69 |
12,98% |
1,07 |
1,17 |
4 |
5 |
|
C |
39,57 |
64,29 |
16,68% |
1,23 |
1,38 |
4,25 |
3 |
|
D |
50,74 |
93,20 |
15,10% |
1,20 |
1,37 |
5 |
7 |
Таблица 4: Нормализованная матрица принятия решений
| Проект |
К1 |
К2 |
К3 |
К4 |
К5 |
||
|
w1 |
b1 |
|
w3 |
b3 |
|||
|
A |
0,149 |
0,245 |
0,267 |
0,241 |
0,266 |
0,232 |
0,167 |
|
B |
0,079 |
0,187 |
0,212 |
0,216 |
0,236 |
0,232 |
0,278 |
|
C |
0,214 |
0,347 |
0,273 |
0,248 |
0,277 |
0,246 |
0,167 |
|
D |
0,274 |
0,504 |
0,247 |
0,242 |
0,276 |
0,290 |
0,389 |
Далее происходит корректировка нормализованной матрицы на значимость конкретного критерия. Результаты взвешивания представлены в таблице 5.
Таблица 5: Взвешенная нормализованная матрица принятия решений
| Проект |
К1 |
К2 |
К3 |
К4 |
К5 |
||
|
w1 |
b1 |
w3 |
b3 |
||||
|
A |
0,067 |
0,110 |
0,056 |
0,026 |
0,029 |
0,028 |
0,018 |
|
B |
0,036 |
0,084 |
0,045 |
0,024 |
0,026 |
0,028 |
0,031 |
|
C |
0,096 |
0,156 |
0,057 |
0,027 |
0,030 |
0,030 |
0,018 |
|
D |
0,123 |
0,227 |
0,052 |
0,027 |
0,030 |
0,035 |
0,043 |
Расчет сумм максимизирующих и минимизирующих критериев осуществляется согласно формулам представленных в методике расчета. Следующем этапом является ранжирование альтернатив по их относительному весу и определение наилучших вариантов. Результаты представлены в таблице 6.
По результатам расчета, мы видим, что проект D – наилучшая альтернатива из четырех представленных с наивысшим относительным весом Qi.
Таблица 6: Итоговая матрица принятия решений
|
Проект |
Максимизирующие критерии |
Минимизирующие критерии |
||||||
|
Дискр |
Интерв |
Сумма |
Дискр |
Интерв |
Сумма |
Qi |
Рейтинг |
|
|
A |
0,056 |
0,117 |
0,173 |
0,046 |
0 |
0,046 |
0,241 |
3 |
|
B |
0,045 |
0,085 |
0,129 |
0,058 |
0 |
0,058 |
0,184 |
4 |
|
C |
0,057 |
0,155 |
0,212 |
0,048 |
0 |
0,048 |
0,279 |
2 |
|
D |
0,052 |
0,203 |
0,255 |
0,078 |
0 |
0,078 |
0,296 |
1 |
Метод, предложенный в рамках данной статьи, объединяет в себе компоненту многокритериальности с компонентой неопределенности среды при реализации инвестиционных проектов. Однако существует ряд ограничений. В частности, представляется проблематичным идеально спрогнозировать поведение проекта в процессе реализации, распределить значимость критериев и определить уровень риска. Компонента субъективности присутствует в любом инвестиционном проекте и во многом определяет качество предлагаемой оценки.
Процесс отбора инвестиционного проекта чрезвычайно важный аспект для компании, ведь именно это решение окажет непосредственное влияние на ее будущее. Поэтому использование научных методов является необходимым условием для достижения достаточного уровня надежности оценки. Снижение компоненты субъективности – первоочередная задача для руководителя, ответственного за принятие решения.
Читайте также
Библиографический список
- Zavadskas, E.K., Kaklauskas, A., Sarka, V. The new method of multicriteria complex proportional assessment of projects. Technological and Economic Development of Economy, 1(3): 131-139, 1994.
- Oliveira, F., Volpi, N., & Sanquetta, C. Goal programming in a planning problem. Applied Mathematics and Computation, 140: 165-178, 2003.
- Ginevicius, R. Normalization of quantities of various dimensions. Journal of Business Economics and Management, 9(1): 79-86, 2008.
- Ustinovichius, L., Zavadskas, E.K., Podvezko, V. Application of a quantitative multiple criteria decision making (MCDM-1) approach to the analysis of investments in construction. Control and Cybernetics, 36(1): 251–268, 2007.
- Hwang, C.L. and Yoon, K. Multiple attribute decision making: Methods and applications. Berlin: Springer Verlag, 1981.
References
- Zavadskas, E.K., Kaklauskas, A., Sarka, V. The new method of multicriteria complex proportional assessment of projects. Technological and Economic Development of Economy, 1(3): 131-139, 1994.
- Oliveira, F., Volpi, N., & Sanquetta, C. Goal programming in a planning problem. Applied Mathematics and Computation, 140: 165-178, 2003.
- Ginevicius, R. Normalization of quantities of various dimensions. Journal of Business Economics and Management, 9(1): 79-86, 2008.
- Ustinovichius, L., Zavadskas, E.K., Podvezko, V. Application of a quantitative multiple criteria decision making (MCDM-1) approach to the analysis of investments in construction. Control and Cybernetics, 36(1): 251–268, 2007.
- Hwang, C.L. and Yoon, K. Multiple attribute decision making: Methods and applications. Berlin: Springer Verlag, 1981.






