Количественный подход к анализу влияния совокупности рисков на инвестиционный проект
Quantitative method of analysis of the impact of the set of risks on the investment project

Авторы
Аннотация
В работе представлен количественный подход к оценке влияния совокупности рисков на финансовые результаты инвестиционного проекта. В основу положен расчет функций чувствительности для выбранной целевой функции проекта в пределах заданного горизонта планирования. Далее с помощью теории нечетких множеств определяются математические ожидания границ относительных отклонений целевой функции при нечетких оценках риск-параметров. Представлен пример результатов риск-анализа конкретного инвестиционного проекта. Показаны преимущества предложенного метода перед широко известными подходами.
Ключевые слова
риски, риск-анализ, функции чувствительности, теория нечетких множеств, инвестиционный проект
Рекомендуемая ссылка
Котов Виктор Иванович. Количественный подход к анализу влияния совокупности рисков на инвестиционный проект // Современные технологии управления. ISSN 2226-9339. — №7 (43). Номер статьи: 4306. Дата публикации: 08.07.2014. Режим доступа: https://sovman.ru/article/4306/
Authors
Abstract
This paper presents new quantitative procedure to estimate finance results of the set of risks influence on the investment projects. This procedure based on sensitive functions and fuzzy set theory. In result we have expectation of border deviation of the objective function of the investment project. There is example of telecommunication project risk-analysis. The advantages of this method over other procedures are discussed.
Keywords
Risks, Risk-analysis, Sensitive functions, Fuzzy Set theory, Investment project
Suggested citation
Kotov Viktor Ivanovich. Quantitative method of analysis of the impact of the set of risks on the investment project // Modern Management Technology. ISSN 2226-9339. — №7 (43). Art. # 4306. Date issued: 08.07.2014. Available at: https://sovman.ru/article/4306/
Введение
Во многих работах (например, [1, 5, 6, 7, 8] и др.), посвященных риск-анализу, к количественным методам, как правило, относят метод сценариев, имитационное моделирование и анализ чувствительности проекта к отклонению параметров. Недостатком последнего авторы, чаще всего, считают его однофакторность, т.е. определение чувствительности по каждому риску в отдельности, и его непригодность в ситуациях одновременного воздействия множества рисков или их взаимной зависимости. Указания на эти «недостатки» почти дословно кочуют из публикации в публикацию без каких-либо конкретных примеров и доказательств.
Кроме того, практически во всех публикациях доминируют так называемые вероятностные методы количественных оценок риска, основанные на задании неких гипотетических вероятностей состояний окружающей бизнес среды. Как было показано в работах [9, 13], эти вероятности принципиально не могут быть определены, т.к. классическая теория вероятностей не работает в экономических системах, где люди принимают решения. Ссылки на какие-либо субъективные экспертные оценки указанных вероятностей на наш взгляд не являются убедительными. Альтернативой вероятностному подходу является теория нечетких множеств Лотфи Заде [8, 10] и развиваемая на ее основе теория возможностей [11]. В данной статье мы покажем, как на основе функций чувствительности и теории нечетких множеств можно построить количественный метод анализа влияния совокупности рисков.
Ниже на рис. 1 показан алгоритм риск-анализа, в основе которого лежит известная модель денежных потоков инвестиционного проекта. Здесь приняты следующие обозначения:
Xsq(t) + Dx(t) – плановые (расчетные) значения вектора риск-параметров (Statusquo) и его отклонение вследствие воздействия рисков.
Ysq(t) + Dy(t) – плановое (расчетное) значение целевой функции (Statusquo) и ее отклонение под влиянием рисковых событий.
![]() – функция чувствительности целевой функции Y по риск-параметру xi .
– функция чувствительности целевой функции Y по риск-параметру xi .
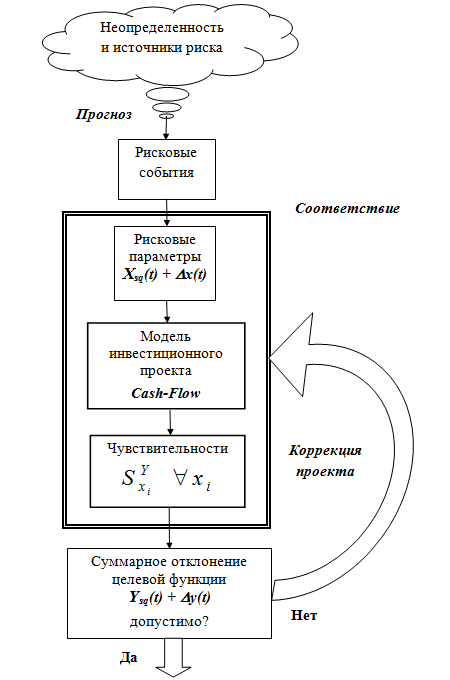
Рис. 1. Алгоритм анализа влияния совокупности рисков
1. Модель и методика нечеткой оценки влияния совокупности рисков
Модель нечеткого относительного отклонения целевой функции может быть построена на основе формулы полного дифференциала [2] функции N переменных (линейная часть разложения в ряд Тейлора):
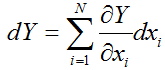 , (1)
, (1)
из которой следует формула полного относительного отклонения данной функции
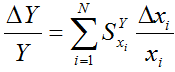 , (2)
, (2)
выраженная через соответствующие функции чувствительности
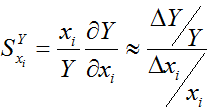 , (3)
, (3)
по каждому из N рисков. Здесь риск-параметры, целевая функция и функции чувствительности являются динамическими характеристиками, т.е. зависят от времени. Для простоты обозначений в дальнейшем параметр времени будем опускать. Поскольку рисковые события могут быть как краткосрочными, так и долгосрочными, то соответствующие им функции чувствительности могут быть локальными и глобальными, соответственно [3].
Для количественной оценки влияния совокупности рисков воспользуемся теорией нечетких множеств, как наиболее адекватному подходу по сравнению с вероятностными моделями. В этом случае риск-параметры x можно представить нечеткими числами треугольного типа по виду их функций принадлежности, как показано на рис. 2. Эти числа можно задать в явной форме или совокупностью α–уровневней.
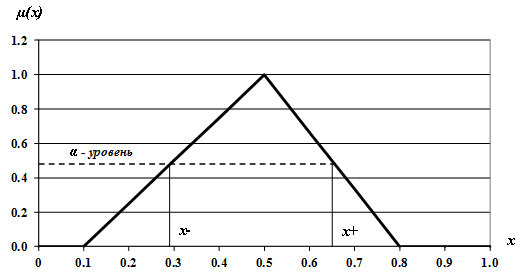
Рис. 2. Функция принадлежности треугольного типа для нечеткого числа х
Переходя к относительным отклонениям риск-параметров x, входящих в формулу (2), последним также будут соответствовать нечеткие числа треугольного типа (рис. 3). Вершины треугольников всех указанных нечетких чисел будут находиться в начале координат, т.е. при Δх/x=0.
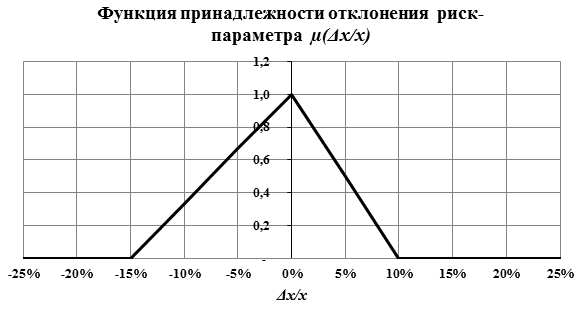
Рис. 3. Пример нечеткого относительного отклонения риск-параметра
Если все относительные отклонения риск-параметров будут нечеткими числами треугольного типа, то и относительное отклонение целевой функции Y будет нечетким числом того же типа для любого момента времени в силу линейности модели (2), при чем вершина треугольника нечеткого относительного отклонения целевой функции будет при Δy/y=0 , как показано на рис. 4.
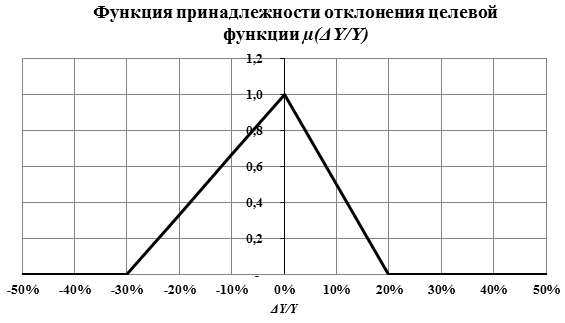
Рис. 4. Пример нечеткой целевой функции треугольного типа
Для нахождения наибольшего нечеткого относительного отклонения целевой функции Y с помощью α–уровневого принципа обобщения [13] достаточно рассмотреть лишь один уровень при α = 0. Это будет соответствовать наибольшей ширине интервала неопределенности целевой функции, ( – 30% и +20%, как показано на рис. 4).
Методика риск-анализа может быть следующей. Для каждого нечеткого относительного отклонения риск-параметра х с помощью экспертных оценок или на основе прошлого опыта определим предельные границы интервалов неопределенности:
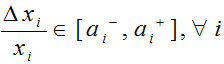 , (4)
, (4)
Тогда, нечеткое относительное отклонение целевой функции при воздействии совокупности рисков будет:
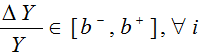 , (5)
, (5)
где нижняя и верхняя границы будут, соответственно:
![]() , (6)
, (6)
и
![]() . (7)
. (7)
Данный метод расчетов гарантирует, что при любых вариациях риск-параметров, заданных в пределах (4), отклонение целевой функции не выйдет за пределы интервала неопределенности (6 и 7). Если рассчитывать границы отклонений целевой функции Y треугольного вида при α ≠ 0, то границы интервалов неопределенности риск-параметров в (4) необходимо выбрать как:
![]() . (8)
. (8)
2. Пример нечеткого анализа влияния совокупности рисков
Нами был рассмотрен проект, связанный с развитием сети некоторого оператора связи. Инвестиции делались в новое оборудование и в расширение имеющейся сети, что позволило предложить абонентам новые услуги. Была построена модель Cash-Flow проекта, на основе которой проведен анализ влияния совокупности рисков. Горизонт планирования был равен пяти годам, а шаг планирования одному кварталу.
Рассматривались три основные группы рисков: колебания натуральных объемов продаж услуг, отклонения текущих издержек и инвестиционных затрат. Всего оценивалось влияние 26-ти рисковых событий. В качестве примера для различных значений α–уровней были выбраны границы интервалов неопределенности (∆x/х– , ∆x/х+) относительных отклонений риск-параметров, показанные в таблице ниже.
Таблица 1. Интервалы неопределенности для риск-параметров
| Риск-параметр |
α = 0 |
α = 0,5 |
α = 1,0 |
||
|
∆x/х– |
∆x/х+ |
∆x/х– |
∆x/х+ |
∆x/х– =∆x/х+ |
|
| Натуральные объемы продаж услуг связи |
–10% |
+5% |
–5% |
+2,5% |
0% |
| Текущие издержки |
–2% |
+5% |
–1% |
+2,5% |
0% |
| Инвестиционные затраты |
–2% |
+5% |
–1% |
+2,5% |
0% |
При α = 0 имеем максимальную ширину интервала неопределенности, а при α = 1 ширина указанного интервала равна нулю, что соответствует наиболее возможному событию (функция принадлежности равна единице). Поскольку это два крайних состояния, вероятности которых нам неизвестны, то в соответствии с принципом Байеса мы можем считать их вероятности одинаковыми, т.е. равными 0,5. Вот почему для наших расчетов мы выбрали уровень α = 0,5.
В качестве целевых функций были выбраны:
- накопленное сальдо денежных потоков – ASCF(Т);
- накопленный чистый денежный поток – ANCF(Т), включающий чистую прибыль и амортизационные отчисления.
Далее в пределах всего горизонта планирования с помощью (6 и 7), используя найденные глобальные функции чувствительности, были определены границы доверительных интервалов указанных целевых функций. Результаты расчетов показаны на рисунках ниже.
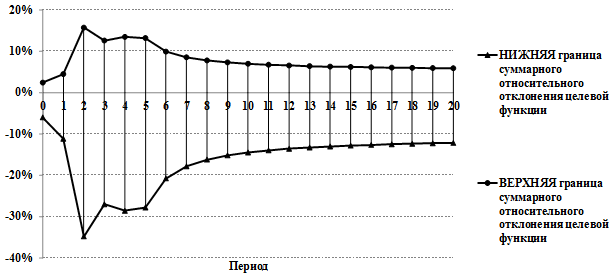
Рис.5. Верхняя и нижняя границы суммарных относительных отклонений накопленного сальдо денежных потоков (ASCF)
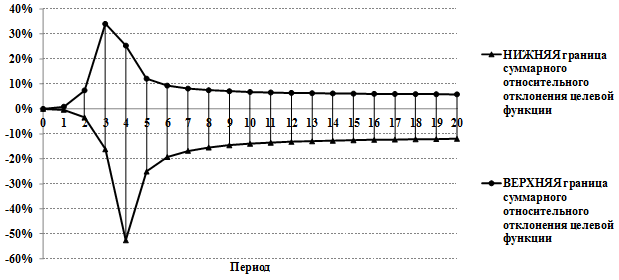
Рис.6. Верхняя и нижняя границы относительных отклонений накопленного чистого денежного потока (ANCF)
Как видно из приведенных на рис.5 и 6 кривых, наиболее «опасными» (рискованными) являются кварталы со 2-го по 6-й (снижение целевой функции ASCF более 20%). Кроме того, из рис. 6 следует, что в 4-м квартале возможно наибольшее снижение накопленного чистого денежного потока. Это объясняется тем, что ANCF становится положительным лишь между третьим и четвертым периодами, в то время как накопленное сальдо денежных потоков (состояние расчетного счета проекта) все это время остается положительным и поэтому менее чувствительно к воздействию рисков. К концу горизонта планирования относительные отклонения обеих целевых функций приближаются друг к другу. Ранжирование рисков по величине вклада в суммарное отклонение целевой функции показало, что на 15 рисков из 26 приходится 90% указанного отклонения.
Полученные границы максимально возможных отклонений целевых функций при воздействии совокупности рисков являются по сути своей оценками на наихудший (отрицательные значения на графике) и наилучший случай (положительные значения на графике). Таким образом, мы получили две крайние оценки: случай позитивного варианта сценария и случай негативного варианта сценария. Эти оценки справедливы, если предположить, что все неприятности (или все позитивные шансы) произойдут непременно.
Однако, практически такая ситуация маловероятна и чем больше рисковых событий мы будем включать в рассмотрение, тем менее возможно, что они все непременно произойдут в одно и тоже время. Далее мы найдем более реалистичные оценки указанных границ с учетом вероятностей появления различных совокупностей из N возможных событий.
3. Оценка вероятности одновременного воздействия случайной комбинации рисковых событий из заданной совокупности рисков
Как известно [2], число комбинаций из N событий по k будет:
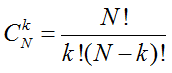 (9)
(9)
Если случайная k-совокупность выбрана из N независимых случайных событий, то вероятность ее появления будет:
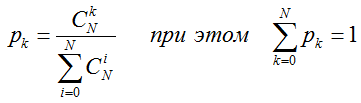 (10)
(10)
Здесь k = 0 соответствует ситуации, когда не произошло ни одно событие из N событий, причем вероятность такого исхода, как следует из (10), будет:
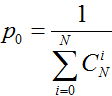 (11)
(11)
Ниже на рис.7 приведено распределение вероятностей, рассчитанных по формуле (10) для N = 10.
Следует заметить, что здесь мы не определяем вероятность значения отдельно взятого рискового события. Если возможные значения рисков образуют континуум, то вероятность каждого из них стремится к нулю. Мы можем априори рассчитать лишь вероятности одновременного появления некоторой случайной совокупности рисковых событий из конечного числа таких совокупностей.
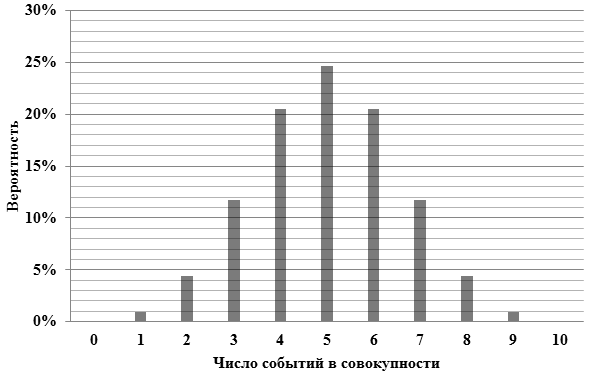
Рис.7. Распределение вероятностей одновременного действия различных совокупностей рисковых событий.
4. Нечеткая оценка математического ожидания границ отклонения целевой функции при одновременном воздействии совокупности рисков
В [4] приведено доказательство ранее сформулированной нами теоремы, из которой следует, что при воздействии на экономическую систему (например, инвестиционный проект) одновременно любой случайной k-совокупности из множества, состоящего из N независимых рисковых событий, математическое ожидание относительного отклонения целевой функции системы (с учетом ее чувствительности к этим рискам) будет вдвое меньше, чем в предположении, что все N рисков будут действовать одновременно (наихудший случай). Иначе говоря, всегда имеет место соотношение:
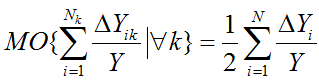 (12)
(12)
где
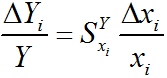 (13)
(13)
Здесь ∆Yi – абсолютное отклонение целевой функции при воздействии i—го риска с интенсивностью ∆xi, а в фигурных скобках в (12) указаны все k-совокупности рисков. Таким образом, с помощью (12) может быть получена более реалистичная оценка влияния совокупности рисков, чем оценка в наихудшем варианте.
С учетом вышеизложенного для анализируемого проекта были рассчитаны новые более реалистичные границы относительных отклонений целевых функций при одновременном воздействии совокупности рисков. Графики математического ожидания верхней и нижней границы суммарного относительного отклонения целевой функции будут в точности повторять кривые, изображенные на рис. 5 и 6 с учетом того, что значения по оси ординат необходимо разделить на два, как следует из (12).
5. Чувствительность и сценарный подход к риск-анализу
В ряде работ по анализу рисков [1, 6, 8] метод сценариев рассматривается как альтернатива анализу чувствительности. При этом авторы, приписывая «однофактороность» методу чувствительностей, делают вывод о том, что последний непригоден для анализа влияния совокупности рисков и вместо него предлагают сценарный подход. На наш взгляд такой вывод неправомерен. Развиваемый нами метод функций чувствительности позволяет с иных позиций смотреть на суть сценарного подхода и существенно дополнить его. С помощью (3) – (7) и модели, показанной на рис.1 можно количественно оценить влияние совокупности рисков для любого сценария развития бизнеса и сравнивать эти сценарии между собой по степени рискованности.
Сценарии могут различаться выбранными стратегиями. Например, одну и ту же бизнес идею можно реализовать:
- приобретая производственные площади в собственность фирмы, либо арендуя последние;
- выбирая различные виды технологий или оборудования;
- решая логистические задачи с помощью организации собственного транспортного подразделения, либо арендуя транспортные средства;
- выбирая различные альтернативные каналы сбыта; и т.д.
Далее для каждого сценария обычно выделяют три варианта его реализации:
- оптимистический;
- средний (наиболее возможный);
- пессимистический.
Эти варианты будут различаться предельными оценками значений риск-параметров, которые могут принимать благоприятные или неблагоприятные для бизнеса величины. Если выбранная целевая функция (например, NPV) явно зависит от указанных параметров, то можно без расчета чувствительностей оценить значение этой функции в наилучшем (шанс) и в наихудшем (риск) случае. Заметим, что такой анализ будет весьма грубым и не вполне реалистичным. Кроме того, он не позволяет судить о динамике влияния рисков, не дает возможности выявить наиболее рискованные периоды «жизни» бизнеса, не позволяет оперативно сравнивать влияние различных факторов риска между собой.
Корректную количественную оценку рискованности каждого сценария и его вариантов можно сделать с помощью предложенного нами метода функций чувствительности в сочетании с теорией нечетких множеств. Если имеются подходящие модели Cash-Flow для выбранных сценариев, то риск-анализ может быть проведен весьма оперативно и в полном объеме.
Заключение
Предложенный подход к анализу влияния совокупности рисков на основе функций чувствительности и нечетких множеств позволяет в пределах всего горизонта планирования:
- ранжировать риски на основе количественных критериев, выделяя среди них наиболее существенные;
- выявлять будущие наиболее «опасные» периоды «жизни» проекта и оценивать предельно-допустимые значения риск-параметров для указанных периодов, которые необходимы в качестве индикаторов для эффективного управления ходом реализации проекта;
- количественно оценивать влияние совокупности рисков на проект;
- оптимизировать финансовый прогноз в пространстве возможных сценариев и имеющихся степеней свободы проекта с целью минимизации влияния рисков;
- сравнивать различные сценарии одного и того же проекта или различные проекты между собой по степени их рискованности.
Для ситуаций, когда рисковые события являются взаимозависимыми, автором в [4] была предложена модель функций чувствительностей второго порядка, которая позволят учесть не только указанную взаимозависимость, но и применять данный подход в ситуациях, когда нельзя пренебречь нелинейностью модели Cash-Flow. Таким образом, была полностью доказана несостоятельность существующей критики метода чувствительностей.
Читайте также
Библиографический список
- Асаул В.В. и др. Минимизация рисков формирования эффективных интеграционных образований в инвестиционно-строительной сфере. – СПб, Изд-во АНО «ИПЭВ», 2011, – 364 с.
- Корн Г., Корн Т. Справочник по математике для научных работников. Пер с англ. под ред. И.Г.Абрамовича. – М.: Наука, 1968. – 720 с.
- Котов В.И. Анализ рисков инвестиционных проектов на основе функций чувствительности и теории нечетких множеств. – СПб, «Судостроение», 2007. – 128 с.
- Котов В.И. Риск-анализ на основе функций чувствительности и теории нечетких множеств. 2-е издание. СПб, ЦНИТ «АСТЕРИОН», 2014. – 218 с.
- Ларсон Э.У. Грей К.Ф. Управление проектами. Учебник. Пер. с англ. – М.: Изд-во «Дело и Сервис», 2013 – 784 с.
- Риск-анализ инвестиционного проекта: Учебник для вузов / под ред. М.В.Грачевой. – М.: ЮНИТИ-ДАНА, 2001. – 351 с.
- Управление проектами. Учебное пособие для студентов обучающихся по специальности «Менеджмент организации»/ И.И.Мазур и др. под общ. ред. И.И.Мазур и В.Д.Шапиро. 10-е изд. стер. – М.: Изд-во «Омега-Л», 2014 – 960 с.
- Шапкин А.С., Шапкин В.А. Теория риска и моделирование рисковых ситуаций. Учебник – 5-е изд. – М.: Издательско-торговая корпорация «Дашков и К°», 2012 – 880 с.
- Zadeh L.A. Fuzzy Sets as a Basis for a Theory of Possibility // Fuzzy Sets and Systems. – 1978. – Vol.1, № 1.
- Кофман А. Введение в теорию нечетких множеств. – М.: Радио и связь, 1982. – 432 с.
- Нечеткие множества и теория возможностей. Последние достижения/Под ред. Р.Р. Ягера.-М.: Радио и связь, 1986. – 408 с.
- Zimmerman H.-J. Fuzzy Sets Theory – and Its Applications. – Kluwer Academic Publishers, 2001.
- Недосекин А.О. Методологические основы моделирования финансовой деятельности с использованием нечетко-множественных описаний. Диссертация на соискание ученой степени доктора экономических наук. СПб, СПбГУЭФ, 2004. – Также на сайте: http://www.mirkin.ru/_docs/doctor005.pdf .
References
- Asaul V.V. Minimizing risks and other building effective integration structures in the field of investment and construction [Minimizatciia riskov formirovaniia effektivnykh integratcionnykh obrazovanii v investitcionno-stroitelnoi sfere]. St. Petersburg, Academy of ANO “IPEV”, 2011, 364 p.
- Korn G., Korn T. Mathematical Handbook for Scientists [Spravochnik po matematike dlia nauchnykh rabotnikov]. Translated from English. ed. I.G.Abramovicha. Moscow, Nauka, 1968. 720 p.
- Kotov V.I. Risk analysis of investment projects on the basis of the sensitivity functions and the theory of fuzzy sets [Analiz riskov investitcionnykh proektov na osnove funktcii chuvstvitelnosti i teorii nechetkikh mnozhestv]. St. Petersburg, “Shipbuilding”, 2007. 128 p.
- Kotov V.I. Risk analysis based on sensitivity functions and the theory of fuzzy sets [Risk-analiz na osnove funktcii chuvstvitelnosti i teorii nechetkikh mnozhestv]. 2nd edition. St. Petersburg, CNIT “ASTERION” 2014. 218 p.
- Larson E.U. Grei K.F. Project Management [Upravlenie proektami]. Textbook. Lane. from English. Moscow: Publishing House of the “Business and Service”, 2013. 784 p.
- Risk analysis of the project [Risk-analiz investitcionnogo proekta]. Textbook for Universities, ed. M.V.Gracheva. Moscow, UNITY-DANA 2001. 351 p.
- Project Management. Textbook for students enrolled in the specialty “Management of organization” [Upravlenie proektami. Uchebnoe posobie dlia studentov obuchaiushchikhsia po spetcialnosti «Menedzhment organizatcii»]. I.I.Mazur etc. under Society. Ed. I.I.Mazur and VD Shapiro. 10th ed. sr. Moscow, Publishing House of the “Omega-L”, 2014. 960 p.
- Shapkin A.S., Shapkin V.A. Risk theory and modeling of risk situations [Teoriia riska i modelirovanie riskovykh situatcii]. Moscow: Publishing and Trading Corporation “Darya and K °», 2012. 880 p.
- Zadeh L.A. Fuzzy Sets as a Basis for a Theory of Possibility. Fuzzy Sets and Systems. 1978. Vol.1, № 1.
- Kofman A. Introduction to the theory of fuzzy sets [Vvedenie v teoriiu nechetkikh mnozhestv]. M., Radio and communication, 1982. 432 p.
- Fuzzy sets and possibility theory. Recent advances [Nechetkie mnozhestva i teoriia vozmozhnostei. Poslednie dostizheniia]. Ed. R.R. Iager. M., Radio and Communications, 1986. 408 p.
- Zimmerman H.-J. Fuzzy Sets Theory – and Its Applications. Kluwer Academic Publishers, 2001.
- Nedosekin A.O. Methodological bases of financial modeling activities using fuzzy multiple descriptions [Metodologicheskie osnovy modelirovaniia finansovoi deiatelnosti s ispolzovaniem nechetko-mnozhestvennykh opisanii]. Dissertation for the degree of Doctor of Economics. St. Petersburg, StPSUEF 2004. Also on the site: http://www.mirkin.ru/_docs/doctor005.pdf.






