Управление рисками в банковских технологиях кредитования корпораций
The risk management in bank lending technology corporations
Авторы
Аннотация
На основе системного метода структурных преобразований систем разработан оригинальный алгоритм управления рисками в банковских технологиях кредитования юридических лиц (предприятий и компаний). Суть управления рисками заключается в уменьшении ошибок I и II рода при принятии решения об условиях кредитования заемщиков (размерам кредита, параметрах денежного потока по его погашению) на основе объективной оценки кредитоспособности заемщиков. Применяемые инструментарии – нейросети и модели с нечетким описанием.
Ключевые слова
ошибки I и II рода, риски кредитования, модели скоринга, нейросети, нечеткая пентошкала Поспелова.
Рекомендуемая ссылка
Касимова Лиана Ириковна. Управление рисками в банковских технологиях кредитования корпораций // Современные технологии управления. ISSN 2226-9339. — №6 (54). Номер статьи: 5405. Дата публикации: 08.06.2015. Режим доступа: https://sovman.ru/article/5405/
Authors
Abstract
On the basis of a systematic method of structural transformation systems the original algorithm of risk management in banking technology lending entities was developed (businesses and companies). The essence of risk management is to reduce the errors I and II when deciding on the conditions of lending to borrowers (loan size and parameters of the cash flow for repayment) on the basis of an objective assessment of the creditworthiness of borrowers. Application tools - neural network model with a clear description.
Keywords
1 and 2 the error type, credit risks, scoring models, neural networks, fuzzy penta scale of Pospelov.
Suggested citation
Kasimova Liana Irikovna. The risk management in bank lending technology corporations // Modern Management Technology. ISSN 2226-9339. — №6 (54). Art. # 5405. Date issued: 08.06.2015. Available at: https://sovman.ru/article/5405/
1. Введение.
В операциях кредитования, а также последующих операциях управления реструктуризацией кредиторской задолженности, если юридическое лицо не состоянии погасить всю сумму кредита в указанный в договоре срок, важное значение имеет объективная информация о стадиях развивающегося процесса банкротства заемщика. Такая информация может быть получена из математических моделей банкротства, построенных на базе стандартной бухгалтерской отчетности. Здесь есть свои проблемы:
1) Отсутствие единой общепринятой методики отбора экономических показателей (факторов) для модели банкротства.
2) Высокий уровень неопределенности и зашумленности публично доступных баз данных, которые специалисты по моделированию называют базами с «триадой НЕ-факторов» (неопределенности, неточности, неполноты) объясняется тем, что в ряде случаев заемщику выгодно «приукрасить» свое финансово-экономическое состояние в бухгалтерской стандартной отчетности.
3) В связи с бурным развитием наукоемкого высокотехнологического производства, развитием концепции «зеленого» производства порождается глубокая специфика в технологических и финансово-экономических процессах функционирования различных предприятий и компаний. Эта специфика не находит в полном объеме отражения в стандартах бухгалтерского учёта, что создает условия для порождения указанной выше триады «НЕ-факторов» в данных.
Указанные причины стимулируют развитие методов решения задач оценки вероятности риска банкротства как в России, так и за рубежом. В этом развитии можно отметить две тенденции, нашедшие отражение в данной статье:
1) Комплексирование различных методов в одном алгоритме, которое согласно общесистемному закону уменьшения энтропии в общей системе, полученной объединением рационально взаимодействующих подсистем, порождает различные эмерджентный эффект, улучшающий алгоритм [1]:
(1)
где 
– объединяемые подсистемы; 
– энтропии изолированных подсистем, которые не обмениваются между собой информацией и материальными потоками; 
— энтропия объединённой системы, которая будет меньше суммы энтропий подсистем 
за счёт появления дополнительных связей, а следовательно и уменьшения числа допустимых состояний объединённой системы 
— это порождаемая при объединении полезная информация (негэнтропия). Привнесение в разработку математической модели такой полезной априорной информации о свойствах искомого решения можно, например, усмотреть в основе теории регуляризации А. Н. Тихонова решения некорректных обратных задач интерпретации данных (аппроксимации) [2].
2) Введение в модель банкротства наряду с количественными, качественных факторов, например, на основе нечёткого описания модели и правил вывода [3].
3) Стремление оценить в модели банкротства стадии развивающегося процесса кризиса компаний и корпораций и, по возможности, сделать временной прогноз стадий банкротства на заданный момент времени t0. Термин «по возможности» здесь употреблен в связи с тем, что динамические модели банкротств с непрерывным временем t практически не разработаны.
Известны две группы методов, которые с той или иной эффективностью, измеряемой долей ошибок I и II рода в оценке риска банкротства, в модели оказываются работоспособными в сложных условиях моделирования оговоренных выше:
- методы нечёткого описания модели и нечётких правил вывода;
- методы нейросетевого моделирования.
В данной статье, которая является обобщением и развитием моделей банкротств из [4], на основе системного закона энтропийного равновесия, иллюстрируемого соотношением (1), предложен оригинальный алгоритм комбинации нейросетевого метода прогноза индикаторов банкротства и метода нечеткой оценки стадии банкротства.
2. Идея предлагаемого гибридного алгоритма
В предлагаемом гибридном алгоритме эффективность прогнозных нейросетевых моделей индикаторов банкротства (факторов) базируется на высокой прогностической силе нейросетей [5]. Однако нейросеть не объясняет, как достигается результат прогноза, за счёт какого именно механизма. С другой стороны, нечеткая модель вывода о вероятности риска банкротства оперирует с понятными для человека лингвистическими терминами и объясняет, за счёт каких именно экономических показателей (их в модели 16) снижается (либо увеличивается) риск банкротства анализируемого объекта. Как известно из теории систем [1], удачная комбинация методов порождает синергетический эффект, т.е. взаимно усиливает объединяемые методы.
Предлагается декомпонировать задачу оценки кредитоспособности совокупности объектов-предприятий на две подзадачи:
1) Групповой скоринговой оценки в виде кластеризации объектов (внутри образуемых кластеров предприятия считается приближенно однородными в аспекте их кредитоспособности).
2) Индивидуального углублённого анализа средних и крупных «проблемных» по итогам кластеризации предприятий, либо предприятий, выбираемых из кластеров экспертно.
После решения обеих подзадач, полученные результаты используется в гибридном (комплексном) алгоритме поддержки разработки и принятия решения по управлению процессом кредитования, включая его заключительные стадии объявления заемщика банкротом либо реструктуризации его долга.
Подзадача 1 решается с помощью универсальных нейросетевых кластеризаторов [5] — самоорганизующихся карт Кохонена. Порождаемый здесь эмерджентный эффект — это возможность оперативной экспресс-оценки кредитоспособности относительного большого числа мелких предприятий заемщиков.
Подзадача 2 решается на основе оригинального гибридного нечетко — нейросетевого алгоритма, подробно описанного ниже. Порождаемый гибридизацией эмерджентный эффект, отмеченный выше, состоит в сочетании достаточно высокой доли правильного распознавания объектов назревающего банкротства, обеспечиваемого прогнозной нейростевой моделью, и «прозрачного» механизма интерпретации факторов банкротства, обеспечиваемого нечетким описанием в привычных человеку терминах, с применением «серой» шкалы Д.С. Поспелова [3,6]. При этом факторами банкротства можно управлять с помощью упреждающих воздействий.
Предлагаемый алгоритм для подзадачи 2 состоит из двух частей:
- Оценки прогнозных значений основных экзогенных (объясняющих) переменных с помощью нейросетевой модели одномерных временных рядов.
- Применения правила нечёткого вывода с использованием нечеткой пенташкалы из [3,6], которая подробно описана ниже.
Возможны две модификации предлагаемого алгоритма:
а) для построения модели, оперирующей со всей совокупностью показателей 
б) для построения модели, оперирующей с одним агрегированным обобщенным критериям Ф.
3. Описание предлагаемого гибридного алгоритма (ГА)
Модификация а) ГА
За основу взята спецификация переменных, включающая 16 показателей 
из статьи А.О Недосекина [3], которые легко вычисляются из публично доступной бухгалтерской отчетности для ОАО:
Группа 1 – рентабельность:
R1 – общая рентабельность (балансовая прибыль, отнесённая к разности выручки от продаж и внереализованных доходов, %);
R2 – рентабельность активов (чистая прибыль, отнесённая к средней балансовой стоимости активов, % за квартал);
R3 – рентабельность собственного капитала (чистая прибыль, отнесённая к сумме капитала и резервов (за вычетом собственных акций, выкупленных у акционеров, минус целевое финансирование и поступление плюс доходы будущих периодов), % за квартал);
R4 – рентабельность продукции (прибыль от продаж, отнесённая к выручке от продаж, %);
R5 – рентабельность оборотных активов (чистая прибыль, отнесённая к средней стоимости активов, % за квартал).
Группа 2 – ликвидность и платёжеспособность:
L1 – быстрый коэффициент ликвидности (оборотные активы за вычетом запасов, налога на добавленную стоимость по приобретённым ценностям и долгосрочная дебиторская задолженность), отнесённые к краткосрочным обязательствам (не включая доходы будущих периодов), безразмерная величина);
L2 – коэффициент покрытия запасов (оборотные собственные средства в сумме с краткосрочными займами и кредитами, краткосрочной кредиторской задолженностью, отнесённые к средней величине запасов, %);
P1 – текущий коэффициент ликвидности (оборотные активы за вычетом долгосрочной дебиторской задолженности), отнесённые к краткосрочном обязательствам (не включая доходы будущих периодов), безразмерная величина;
Группа 3 – деловая активность:
A2 – оборачиваемость активов (выручка от продажи (за вычетом налога на добавленную стоимость, акцизов и других обязательств), отнесенная к средней стоимости активов, один раз за квартал);
A4 – оборачиваемость кредиторской задолженности (выручка от продаж без учета коммерческих и управленческих расходов), отнесенная к средней кредиторской задолженности, один раз за квартал);
A5 – оборачиваемость дебиторской задолженности (выручка от продаж за вычетом налога на добавленную стоимость, акцизов и других обязательств, отнесенная к дебиторской задолженности на конец отчетного периода за вычетом задолженности учредителей по вкладом в уставной капитал на конец отчетного периода), один раз за квартал);
A6 – оборачиваемость запасов (себестоимость, отнесенная к средней величине запасов, один раз за квартал).
Группа 4 – финансовая устойчивость:
F1 – коэффициент финансовой зависимости (долгосрочные обязательства в сумме с краткосрочными обязательствами (не включая доходы будущих периодов), отнесенные к капиталу и резервам (за вычетом собственных акций, выкупленных у акционеров минус целевое финансирование и поступления плюс доходы будущих периодов) безразмерная величина);
F2 – коэффициент автономии собственных средств (капитал и резервы за вычетом собственных акций, выкупленных у акционеров минус целевое финансирование и поступления плюс доходы будущих периодов), отнесённые к внеоборотным активам и оборотным активам, безразмерная величина);
F3 – обеспеченность запасов собственными оборотными средствами (собственные оборотные средства, отнесённые к запасам, безразмерная величина);
F4 – индекс постоянного актива (внеоборотные активы в сумме с долгосрочной дебиторской задолженностью, отнесённые к капиталу и резервам (за вычетом собственных акций, выкупленных у акционеров) минус целевое финансирование и поступления плюс доходы будущих периодов), безразмерная величина).
Для качественной и более наглядной интерпретации уровней выбранных показателей необходимо воспользоваться нечеткой – пенташкалой [3], т. е. пятиуровневым классификатором, подробно описанном ниже.
С помощью рассмотренной классификации было выделено пять групп уровня риска (лингвистических термов):
1-я группа – это предприятия очень высокого уровня риска банкротства, которым соответствуют очень низкие уровни классификатора каждого из 16 рассматриваемых параметров (табл. 1);
2-я группа – это предприятия, находящиеся в зоне высокого риска банкротства, которым соответствуют низкий уровень значений классификатора показателей 
;
3-я группа – это предприятия, находящиеся в зоне среднего риска банкротства, соответствующие среднему уровню значений классификатора показателей ;
4-я группа – это предприятия, находящиеся в зоне низкого риска банкротства, соответствующие высокому уровню значений классификатора показателей ;
5-я группа – это кредитоспособные предприятия, которым можно выдать кредит, соответствующий очень высокому уровню значений классификатора показателей .
В [3] для удобства использования пенташкалы при классификации объектов был привлечен экспертный комитет из ведущих специалистов в области финансов и кредита, и для практического пользования была разработана таблица 1.
Используя пенташкалу (Рис.1) для каждого из факторов , в [3] составлена таблица интервалов финансовых показателей, определяющих принадлежность предприятия в той или иной группе, т.е. нечеткому терму 
, 
. На рис. 1 на оси ординат откладываются значения функции принадлежности 
анализируемого четкого значения 
носителя этой функции, т.е. ее аргумента к нечеткому подмножеству 
– интервалу для в таблице 1. Функция принадлежности отражает степень уверенности эксперта в своей оценке. Текущие значения носителя и, предварительно нормированные в отрезок вещественной оси [0;1], откладываются по оси абсцисс. При формировании нечетких термов 
терму конкретное (четкое) значение носителя приписывается к тому терму, у которого ордината соответствующей трапециевидной функции принадлежности окажется большей. Если ординаты функции принадлежности совпадают 
, то значение показателя относится к «более низкому» лингвистическому уровню (терму) из них.
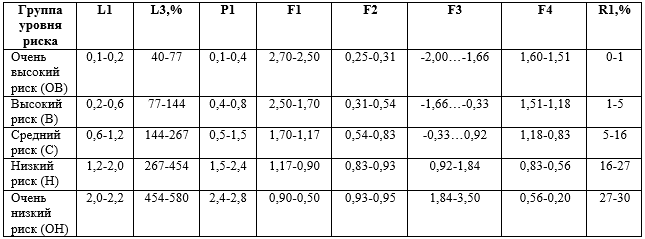
Таблица 1 − Диапазон значений экономических показателей по группам уровня риска
Окончание таблицы 1
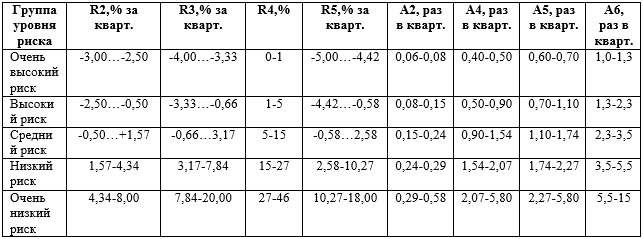
В табл. 1 приведен диапазон значений финансовых показателей, соответствующих каждому из уровней кредитоспособности предприятия, определенный экспертно.
Из 16 представленных показателей значения F1 и F4 являются инверсными по отношению ко всем остальным показателям, так как с ростом количественных уровней этих параметров финансовое положение предприятия ухудшается, а уровень риска банкротства увеличивается, следовательно, для соблюдения условия одноправленности всех показателей надо преобразовать F1 и F4, например:
(1)
Методика использования таблицы 1 очень проста: если есть исторические данные по указанным выше 16 показателей 
, то с использованием универсального нейросетевого аппроксиматора [5] аппроксимируются временные ряды и находятся прогнозные значения всех 16 показателей 
для планируемого периода 
. В количественных оценках мы использовали нейросеть типа «многослойный персептрон» (Multi Lauer Perseptron (MLP)) с алгоритмом обучения типа «обратного распространения ошибки» (Back Propagation (BP)). Для ответственных объектов кредитования модель была усилена алгоритмом байсовской регуляризации нейросетей, где на байесовском ансамбле варьировалась архитектура сети и активационные функции нейронов скрытых слоев [4].
Прогнозные значения 
подставляются в таблицу 1 и определяется значения уровней риска для предъявляемого объекта, т.е. производится распознавание «образа банкротства» с помощью правил нечеткого вывода.
Затруднение возникает только в двух случаях:
1) Разные показатели 
, относят предъявляемый объект к разным уровням риска, т.е. при сильном зашумлении исторических данных (и даже их сознательном искажении, что иногда наблюдается у предприятий – заемщиков) часть критериев 
относят объект, например, к «высокому уровню риска», а другая часть – к «низкому уровня риска» банкротства.
Возникает неприятная неопределенность. Конечно, если большинство 
критериев из 16 классифицирует объект одинаково, можно ввести вероятный критерий оценки:
, (2)
где 
– допустимая вероятность принятия решения.
2) Хуже обстоит дело, если в исторических данных отсутствует информации по части критериев 
. Тогда использование таблицы 1 становится невозможным для классификации или ранжирования объектов в будущем 
, т.е. в планируемом периоде, либо следует редуцировать таблицу по показателям, чтобы она стала комплектной.
Оба указанных недостатка устраняются при обобщении в виде модификации предлагаемого алгоритма б).
Модификация алгоритма б) с оперированием одним обобщенным показателем
Идея предлагаемой модификации алгоритма б) для подзадачи 2 состоит в том, чтобы агрегировать все 16 (либо любую часть из 16) показателей 
в один обобщенный показатель Ф, например, обобщенную функцию желательности Харрингтона [7].
Решение принимается с помощью нечеткого правила вывода по функции принадлежности [3] (пентошкале), показанной на рис. 1.
Прогнозные значения частных показателей 
, как указывалось выше, целесообразно находить с помощью нейросетевого аппроксиматора [5].
4. Использование нечеткой «серой» пентошкалы Д.С. Поспелова
Все уровни экономических 
могут измеряться не только количественно, но и качественно [6]. В этом случае необходимо определить лингвистическую переменную X = «Уровень риска банкротства», носителем которой является область определения функции Х, которая обычно нормируется в отрезок [0;1]. Терм-множество значений лингвистической переменной X составляют нечеткие подмножества «Очень низкий уровень (ОН)», «Низкий уровень (Н»), «Средний уровень (С)», «Высокий уровень (В)», «Очень высокий уровень(ОВ)». Эта пенташкала является оптимальной в большинстве практических случаев. Для пенташкалы необходимо построить систему функций принадлежности носителя и лингвистической переменной Х, соответствующим нечетким подмножествам – термам 
.
Простейшим способом задания является система трапециевидных нечетких чисел (рис. 1), где по оси абсцисс откладывается значения носителя Х, а по оси ординат – функция принадлежности 
.
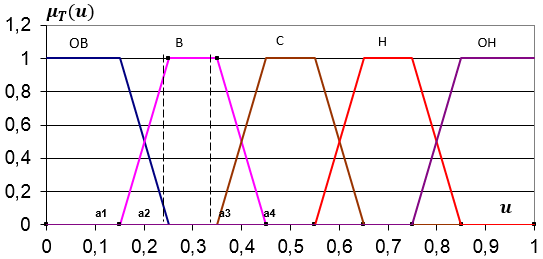
Рис. 1 Пенташкала на трапециевидных числах
Непротиворечивость такого классификатора достигается, если он является серой шкалой в смысле Д.С. Поспелова. [6] В этом случае все соседние трапеции шкалы пересекаются друг с другом в точке с ординатой 0,5. Тогда нарастание силы одного из качественных признаков (показателей) сопряжено с соответствующим убыванием (в том же темпе) смежного качественного признака, а в точке µ = 0,5 достигается максимум информационной неопределенности, и в ней соседние качественные свойства обладают одинаковой силой (различимостью).
Посередине верхних оснований трапеций классификатора (гранулятора) можно отметить точки, абсциссы которых называются здесь узловыми точками. Абсциссы этих точек (числа 
) могут использоваться в дальнейшем как система весов при агрегировании нечетко определенных данных. Например, для рис. 1 узловые точки образуют вектор
(3)
В результате нечеткой классификации можно каждой точке на области определения носителя лингвистической функции Х сопоставить вектор 
, где N – число гранул шкалы (в описанном случае N=5), 
– значение уровня j-ой функции принадлежности. Причем для серой шкалы Д.С. Поспелова выполняется условие
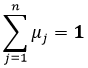(4)
так как шкала Д.С. Поспелова – непротиворечивый и полный классификатор.
Например, для случая рис. 1 выполняется
(5)
Соотношение (4) как раз и выражает результат нечеткого распознавания уровня носителя 
.
Приведенную на Рис. 1 пенташкалу А.О. Недосекин называет «Стандартным пятиуровневым 01 – классификатором», который задает семейство функций принадлежности, осуществляя ассоциацию нечеткого лингвистического описания на ось абсцисс ([0;1] – носитель исследуемого показателя Х).
Пусть некоторое свойство экономического объекта (финансовая устойчивость предприятия, инвестиционная привлекательность ценной бумаги, уровень менеджмента управляющей компании, рыночная привлекательность земли под застройку и т.п.) может быть представлено как древовидная иерархия факторов, причем:
- в рамках иерархии определены системы отношения предпочтения одних подсвойств другим для фиксированного уровня иерархии;
- подсвойства, составляющие низовые звенья иерархии, могут быть измерены как количественно, так и качественно (в том числе словесно).
В этом случае, можно осуществить комплексную оценку силы базового свойства, если:
- производить все измерения на качественном базисе, производя нечеткую классификацию количественных факторов по схеме, изложенной выше;
- для моделирования систем предпочтения применять системы весов Саати или Фишберна [3];
- производить комплексирование качественных уровней факторов в рамках двумерной (матричной) свертки [3], где одной из систем весов выступают веса предпочтений факторов, а другой системой весов – узловые точки классификатора вида (3).
Когда уровень силы комплексного свойства, нормированный на некотором стандартном носителе (например, 01-интервале), получен, можно произвести распознавание качественного уровня данного комплексного свойства на основе соответствующего нечеткого классификатора.
Количественное значение обобщенного (агрегированного) показателя определяется по формуле двойной матричной свертки:
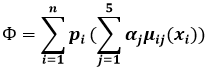(6)
где 
– веса (Фишберна и Саати) i-го показателя в свертке; 
– количество альтернатив, расположенных в порядке убывающего предпочтения; 
– значение функции принадлежности j-го качественного уровня относительно «текущего» значения i-го показателя.
Схема весов Фишберна реализует OWA – оператор Ягера (Ordered Weighted Averaging).
В схеме Фишберна предпочтения на иерархической схеме при переходе от одного фиксированного иерархического уровня к другому изменяются на 1. Веса снижаются по правилу арифметической прогрессии весов:
(7)
Если предпочтения нет, то системе безразличных весов соответствует формула:
(8)
То есть предпочтения по Фишберну согласно (7) выражается в убывании на единицу числителя рациональной дроби весового коэффициента более слабой альтернативы.
Чтобы определить набор весов Фишберна для смешанной системы предпочтений, когда, наряду с предпочтениями, в систему входят отношения безразличия, необходимо определять числители 
рациональных дробей по рекурсивной схеме:
(9)
где 
— знак эквивалентности; 
— знак предпочтения.
Тогда сумма полученных числителей и есть общий знаменатель дробей Фишберна:
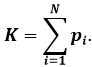(10)
5. Результаты количественных оценок предлагаемого алгоритма
В качестве примера в таблице 2 приведен фрагмент аппроксимации и прогнозирования объясняющих переменных (16 критериев) на 3 квартала вперед для одного крупного предприятия сельскохозяйственного сектора Республики Башкортостан (кодовый номер 30 в выборке из тридцати предприятий)[4].
Прогнозные значения подставляются в таблицу 1 и определяется значение уровня риска банкротства для предъявляемого объекта, т.е. производится распознавание «образа банкротства» с помощью правил нечеткого вывода.
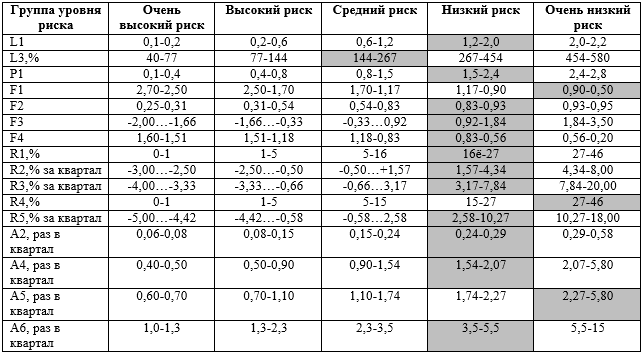
В таблице 3 приведен фрагмент расчетов попадания одного из предприятий-заемщиков образованных кластеров в подзадаче 1 в диапазон значений финансовых показателей, соответствующих каждому из уровней финансового состояния предприятия, определенных экспертно (интервалы попадания выделены цветом). Как видно из таблицы 3, анализируемое предприятие 30 принадлежит к классу низкого риска банкротства, что было подтверждено экспериментальными наблюдениями в производственных условиях межрайонной налоговой инспекции.
Таблица 2. Фрагмент прогноза объясняющих переменных для предприятия 30.
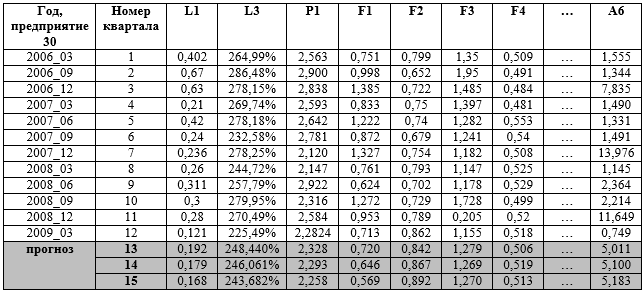
Таблица 3. Интерпретация прогнозных значений показателей (темным цветом выделены интервалы принадлежности для 13-го квартала), анализируемого предприятия №30
6. Выводы
1. Предложен оригинальный алгоритм диагностики стадий банкротства предприятий, в котором на основе общесистемного закона уменьшения энтропии в объединенной системе 
и 
по сравнению с суммой энтропий объединяемых подсистем и . При этом в качестве подсистемы выступает нейросетевая прогнозная модель индикаторов (факторов) банкротства (16 показателей А.О. Недосекина), а в качестве подсистемы – нечеткая модель распознавания стадий банкротства. Достигаемый в объединенной системе эффект (, ) эмерджентный (системный) эффект – это получение нечетких оценок при распознавании стадии банкротства анализируемого предприятия, интерпретируемых в привычных для кредитного эксперта лингвистических терминах.
2. Предложенный алгоритм успешно апробирован на серии экспериментальных наблюдений для 30 сельскохозяйственных предприятий Республики Башкортостан Стерлитамакского района.
3. Предлагаемый алгоритм позволяет весьма оперативно оценить финансовое состояние предприятия-заемщика с контролируемой вероятностью. В нашем примере с вероятностью 0,94 оценка риска банкротства предприятия 30 находится в интервале «низкий-очень низкий». Ценным свойством этого подхода является широкий спектр показателей, участвующих в оценке. С учетом их взаимосвязи, что характерно для экономического объекта, получаем достаточно полную картину оценки.
4. В предложенном алгоритме делается отказ от жестких требований в базе данных, накладываемых классическим методом наименьших квадратов (МНК), применяемым в регрессионном анализе. В различных модификациях МНК, которые мало меняют указанные требования, они называются «предпосылками МНК». В частности трудновыполнимой предпосылкой МНК является гипотеза о нормальном законе распределения случайных ошибок расчета по модели.
5. Переход к нейросетевому инструментарию, свободному от этих предпосылок, в предлагаемом алгоритме имеет и свой недостаток – пропадает возможность оценки адекватности получаемой модели, опирающаяся на проверку статистических гипотез о выполнении предпосылок МНК. Однако, как показали вычислительные эксперименты, оценку адекватности модели можно строить на основе байесовского подхода. При этом достигается также и регуляризация прогнозной модели каждого из 16 индикаторов банкротства.
Читайте также
Библиографический список
- Прангишвили И.И. Системный подход и общесистемные закономерности: Монография.- М.: СИНТЕГ, 2000. – 522с.
- Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. – М.: Наука. Физмалит, — 1986. – 288 с.
- Недосекин А. О. Комплексная оценка риска банкротства корпорации на основе нечетких описаний. – URL: http://sedok.narod.ru/sc-group/html/ дата обращения 15.12.2013).
- Горбатков С.А., Полупанов Д. В., Макеева Е. Ю., Бирюков А. Н. Методологические основы разработки нейросетевых моделей экономических объектов в условиях неопределённости: Монография. – М.: Издательский дом «Экономическая газета», 2012. – 494 с.
- Хайкин С. Нейронные сети: полный курс. Учебник/ 2-ее издание: Пер. с англ. – М.: Издательский дом «Вильямс», 2006. – 1104 с.
- Поспелов Д. С. «Серые» и/или «черно-белые» шкалы // Прикладная эргономика. Специальный выпуск «Рефлексивные процессы». – 1994. — №1. – 36 с.
- Адлер Ю. П., Маркова Е. В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий / Изд. 2-е доп. и перераб. – М.: Наука, 1976. – 278 с.
References
- Prangishvili I. I. System approach and system-wide patterns [Sistemnyj podhod i obshhesistemnye zakonomernosti ]. Monograph M. SINTEG, 2000. 522 p.
- Tihonov A.N., Arsenin V.Ja. Methods for solving ill-posed problems [Metody reshenija nekorrektnyh zadach]. M . Nauka. Fizmalit 1986. 288 p.
- Nedosekin A. O. Comprehensive assessment of risk of bankruptcy corporation based on fuzzy descriptions [Kompleksnaja ocenka riska bankrotstva korporacii na osnove nechetkih opisanij]. URL: http://sedok.narod.ru/sc-group/html/ date treatment 12.15.2013).
- Gorbatkov S.A., Polupanov D. V., Makeeva E. Ju., Birjukov A. N. Methodological basis for the development of neural network models of economic objects in an indefinite [Metodologicheskie osnovy razrabotki nejrosetevyh modelej jekonomicheskih ob#ektov v uslovijah neopredeljonnosti]. monograph. M. Publishing house Economic Newspaper, 2012. 494 p.
- Haykin S. Neural Networks [Nejronnye seti]. A Comprehensive Foundation. Second Edition. M. Wilyms, 2006. 1104 p.
- Pospelov D.S. Grey and or black and white scale [Serye i ili cherno-belye shkaly]. Applied Ergonomics. Special edition of reflexive processes. 1994. №1. 36 p.
- Adler Ju. P., Markova E. V., Granovskij Ju.V. Experimental Design for finding optimal conditions [Planirovanie jeksperimenta pri poiske optimal’nyh uslovij]. Ed. 2nd ext. and rev. M. Nauka, 1976 278 p.
