Применение многоцелевой оптимизации и нечёткой логики для повышения эффективности управления промышленными проектами
Application of multi-objective optimization and fuzzy logic to improve industrial project management efficiency

Авторы
Аннотация
В статье исследуется интеграция методов многоцелевой оптимизации с нечёткой логикой в контексте управления сложными промышленными проектами. Рассматриваются классические методы оптимизации, такие как метод взвешенной суммы, метод уступок и поиск Парето-оптимальных решений, а также их ограничения при работе с качественными и неопределёнными критериями. Предлагается применение теории нечётких множеств и лингвистических переменных для формализации субъективных факторов, включая квалификацию персонала и уровень рисков. На примере оценки интегрального риска демонстрируется эффективность гибридного подхода, сочетающего нечёткую логику с традиционными методами оптимизации. Полученные результаты подтверждают перспективность данных методов для улучшения качества и адаптивности решений в условиях многокритериальности и неопределённости.
Ключевые слова
многоцелевая оптимизация, нечёткая логика, управление промышленными проектами, принятие решений, теория нечётких множеств, лингвистические переменные, оценка рисков, квалификация персонала, Парето-оптимальность, гибридные методы.
Рекомендуемая ссылка
Черекчиди Янис Эримеевич. Применение многоцелевой оптимизации и нечёткой логики для повышения эффективности управления промышленными проектами // Современные технологии управления. ISSN 2226-9339. — №3 (111). Номер статьи: 11106. Дата публикации: 08.09.2025. Режим доступа: https://sovman.ru/article/11106/
Authors
Abstract
The article examines the integration of multi-objective optimization methods with fuzzy logic in the context of complex industrial project management. Classic optimization methods, such as the weighted sum method, the concession method and the search for Pareto-optimal solutions, are considered, as well as their limitations when working with qualitative and uncertain criteria. The application of fuzzy set theory and linguistic variables is proposed to formalize subjective factors, including personnel qualifications and risk level. The effectiveness of a hybrid approach combining fuzzy logic with traditional optimization methods is demonstrated using integral risk assessment as an example. The obtained results confirm the prospects of these methods for improving the quality and adaptability of decisions in conditions of multicriteriality and uncertainty.
Keywords
multi-objective optimization, fuzzy logic, industrial project management, decision making, fuzzy set theory, linguistic variables, risk assessment, personnel qualification, Pareto optimality, hybrid methods.
Suggested citation
Cherekchidi Yanis Erimeevich. Application of multi-objective optimization and fuzzy logic to improve industrial project management efficiency // Modern Management Technology. ISSN 2226-9339. — №3 (111). Art. # 11106. Date issued: 08.09.2025. Available at: https://sovman.ru/article/11106/
Введение
Принятие решений в управлении сложными промышленными проектами является многоцелевой задачей, где требуется учет нескольких критериев одновременно и является непростой задачей, так как требует тщательного анализа различных сочетаний факторов. Если будет выбрано неоптимальное их сочетание, то для крупных промышленных проектов могут наступить серьезные последствия в виде срыва сроков, превышения бюджета и т.д. До недавнего времени основное внимание уделялось принятию оптимальных решений с фокусом на одном критерии, но в таком случае это происходит в ущерб другим критериям. Например, если для принятия решения требуется одновременно учесть факторы: стоимость проекта, сроки проекта, риски, ресурсы и т.д., то, как правило, выделяется один приоритетный, а остальные учитываются по принципу компромисса, где специалисты обходили проблему многокритериальности, фиксируя все критерии, кроме одного, и рассматривая их как ограничения. Оптимизация проводилась лишь по одному критерию, признанному основным. Это означало, что специалист фактически уклонялся от решения сложной задачи выбора множества ограничений. Очевидно, что имеется необходимость в более тонких подходах и аналитических методах для работы с многокритериальными проблемами.
При принятии управленческого решения крайне желательно проанализировать последствия до непосредственного принятия решения с помощью системы поддержки принятия решений, которая помогла бы оценить различные варианты сочетаний факторов и помочь в выборе наиболее эффективного из них. Многокритериальная оптимизация процесса принятия решений подразумевает такой поиск решений, при котором удовлетворяются несколько конфликтующих критериев, что крайне важно для разработки математической модели и последующего программирования.
Многокритериальная задача представляет собой множество вариантов на основе принципов оптимальности, но это не означает, что при решении задачи будет определяться строго максимум или минимум различных критериев. Часто приходится решать задачу при конкретно заданных значениях. В общем случае задача принятия решения – это задача нахождения пары (Ω, P), где Ω – это множество вариантов, а Р – это принцип оптимальности. Решением данной задачи будет являться множество ΩР, принадлежащее к множеству Ω. Наличие исходного множества Ω и принципа оптимальности Р является обязательным, так как без них задача полностью теряет смысл. Элементы множества Ω называются альтернативами, а принцип оптимальности Р – это их наилучшее распределение [1,2].
Для классификации задач принятия управленческих решений используется следующая зависимость:
![]()
где Z – рассматриваемая предметная область,
Ω — перечень альтернатив,
К – критерии оценивания,
S – множество измеряемых параметров по критериям (шкалы),
F – множество оценок для множества альтернатив,
G – система предпочтений,
Р – ключевое правило из системы предпочтений [1].
Однако наибольший интерес представляют задачи многокритериальной оптимизации, где решение приходится принимать не по одному, а сразу по нескольким, иногда противоречивым критериям.
1. Аналитический обзор методов многокритериальной оптимизации
В научной литературе описано достаточно много способов и методов решения задач многокритериальной оптимизации. Рассмотрим наиболее известные из них.
Метод взвешенной суммы (он же метод скаляризации) – это один из самых известных и популярных методов многокритериального принятия решений, который применяется для оценки альтернатив по множеству критериев. Суть метода заключается в присвоении каждому критерию веса, отражающего его важность, и суммировании произведений значений критериев на соответствующие веса. Метод взвешенной суммы прост в реализации и позволяет учитывать относительные приоритеты различных факторов при выборе наилучшей альтернативы. Общий обзор теории и методов многокритериальной оптимизации, включая метод взвешенной суммы описан в работах Ralph E. Steuer [3], Vira Chankong. и Yacov Y. Haimes [4], A. M. Geoffrion [5], среди отечественных авторов наиболее известны работы Подиновского В.В. и Ногина В.Д. [6], Лотова А.В. и Поспеловой И.И. [7], Васильева Ф.П. [8] и многих других
Метод взвешенной суммы, несмотря на свою популярность и простоту, имеет ряд недостатков, которые ограничивают его применение в некоторых сценариях. Например, субъективность в определении весов, предполагаемый характер независимости критериев, игнорирование пороговых значений, трудности с нормализацией данных и др. делают его менее пригодным для ситуаций, связанных с высоким уровнем неопределённости.
Метод уступок применяется в контексте многокритериальной оптимизации, когда задача включает несколько критериев, каждый из которых имеет различную важность для принятия оптимального решения. В таких случаях выбор одного критерия в качестве приоритетного может негативно сказываться на остальных, что делает необходимым находить баланс между различными целями. При применении метода уступок к многокритериальным задачам каждая из сторон (в данном случае — критерии) соглашается на частичное ухудшение своего значения ради улучшения других критериев. В итоге получается компромиссное решение, которое учитывает интересы всех участников процесса, хотя ни один из критериев не достигает своего абсолютного максимума. Данной темой активно занимались Подиновский В.В. и Ногин В.Д. [6], Бродецкий Г. Л., Гусев Д. А., Мазунина О. А. [9], Казанская О.В. [10] и многие другие.
Метод уступок так же, как и метод взвешенной суммы имеет широкую популярность, но при этом тоже имеет существенные недостатки, такие как субъективность выбора уступок, невозможность точного определения оптимального решения, трудоемкость процесса и ограниченную применимость для большого числа критериев.
Метод поиска Парето-оптимальных решений заключается в поиске набора решений, которые обеспечивают оптимальное сочетание нескольких критериев одновременно, причем улучшение одного критерия не должно происходить за счет ухудшения других. Глобально делятся на две категории: эволюционные алгоритмы и метод свертки критериев. Эволюционный метод основан на использовании генетического алгоритма, который работает следующим образом: генерация начальной популяции решений ® создаются новые популяции на основе мутаций ® решения оцениваются относительно новых критериев ® отбираются лучшие решения для формирования следующего поколения. Процесс повторяется до тех пор, пока не будет достигнуто условие остановки.
Метод свертки критериев основан на преобразовании многокритериальной задачи в однокритериальную путем введения дополнительной функции свертки. Один из популярных методов – линейная свертка, где каждый критерий умножается на соответствующий вес и затем они суммируются.
Данному направлению также посвящено большое количество исследований, наиболее известные из которых работа «Экономический расчет наилучшего использования ресурсов» Канторовича Л.В., посвященная использованию методов линейного программирования для решения задач оптимизации, [11], «Основы региональной экономики» Гранберга А.Г., который изучал проблемы оптимального размещения производственных сил и распределения ресурсов [12], «Элементы теории реформ» Полтеровича В.М. [13], Прохоренкова П.А. [14] и многих других.
К основным недостаткам метода можно отнести игнорирование справедливости, неопределенность выбора (так как нет конкретного критерия для выбора между оптимальными решениями), отсутствие учета динамических изменений и невозможность улучшения для всех сразу, так как всегда найдется кто-то, чье состояние останется прежним или ухудшится.
Методы последовательной оптимизации, к которым относятся метод последовательного уточнения критериев и метод последовательного приближения. Суть данных методов заключается в поиске наилучшего решения задачи путем пошагового улучшения текущего результата. Основная идея заключается в том, чтобы начать с некоторого начального решения и постепенно двигаться к лучшему варианту через последовательность улучшений.
Метод последовательного уточнения критериев применяется в многокритериальной оптимизации и подразумевает постепенное уточнение предпочтений ЛПР (лица, принимающего решение). В процессе работы с данным методом человек постепенно сужает область поиска оптимального решения, вводя дополнительные ограничения или предпочтения относительно отдельных критериев. Этот метод помогает лучше понять приоритеты ЛПР и ускорить процесс принятия решения.
Метод последовательного приближения использует пошаговый процесс, чтобы приблизиться к искомому решению, начиная с некоторой начальной точки. Они могут применяться в разных контекстах, например, в численных методах для решения уравнений или оптимизации функций. Например, методы градиентного спуска или методы Ньютона.
Наиболее известные работы, посвященные данной теме: «Математические методы поиска оптимальных решений» Белецкой С.Ю. [15], «Методы оптимизации» Лемешко Б.Ю. [16], «Метод последовательных приближений» Виленкина Н.Я. [17] и др.
Кроме математических методов существует и другой метод, основанный привлечении знаний и опыта специалистов (экспертов), и именно поэтому она получил название экспертного, который предполагает использование субъективной оценки экспертов для определения оптимальных решений. Этот подход особенно полезен в ситуациях, когда невозможно точно описать процесс или систему формальными методами. Недостатки экспертного метода очевидны – это субъективность оценок экспертов, несогласованность мнений и высокая трудоемкость процесса сбора и обработки мнений, но при этом он имеет широкое применение в задачах разработки стратегий развития компании, прогнозирования спроса на продукцию или определения приоритетов в распределении ресурсов [18].
Особого внимания заслуживает применение теории нечётких множеств в решении задач многокритериальной оптимизации. Теория нечётких множеств (fuzzy sets theory), предложенная Лотфи Заде в 1965 году [19], представляет собой мощный подход для моделирования неопределённости и нечёткости в системах принятия решений. Этот метод оказывается особенно полезен в ситуациях, когда информация о рассматриваемых проблемах или переменных является неполной, расплывчатой или субъективной [20].
Поскольку многокритериальные задачи связаны с множеством неопределённых факторов, таких как предпочтения пользователей, экспертные мнения или внешние условия, то применение теории нечётких множеств позволит формализовать такие неопределённости путём введения функций принадлежности, которые позволяют оценивать степень соответствия элементов заданному множеству. Это позволит учесть неполноту знаний и минимизировать потери информации при принятии решений.
Кроме того, применение теории нечётких множеств позволит работать с критериями, которые сложно выразить в числовом виде, например, «высокий», «низкий», «средний» и др., особенно если необходимо агрегировать несколько критериев в единую оценку.
2. Применение теории нечётких множеств для принятия управленческих решений
Алгоритмы на основе нечётких множеств сравнительно просты в реализации и могут быть адаптированы под различные типы задач. Гибкость теории позволяет разработчикам настраивать систему под специфику конкретной проблемы, используя различные функции принадлежности и правила нечёткого вывода. В сложных и многомерных задачах присутствует большое количество взаимосвязанных переменных и критериев, обработка которых представляет определённую алгоритмическую сложность, но даже в таких задачах данная теория помогает структурировать решение. Таким образом, теория нечётких множеств обладает значительными преимуществами перед традиционными методами при решении многокритериальных задач, поскольку она способна эффективно справляться с неопределённостью, обрабатывать качественные данные, улучшать интерпретацию результатов и обеспечивать гибкую и мощную основу для принятия решений [19].
Рассмотрим более подробно применение теории нечётких множеств для решения задач многокритериальной оптимизации в управлении крупными промышленными проектами. Такие проекты отличаются высокой сложностью, большими объемами работ, участием большого числа заинтересованных сторон, значительными финансовыми затратами и большим количеством критериев, которые необходимо учитывать при принятии управленческих решений. Наибольшую важность в таких задачах имеют вопросы управления рисками, которые можно разделить на: технические, финансовые, временные и организационные и которые напрямую оказывают влияние на принятие решения. Каждый из этих рисков, в свою очередь, зависит от целого набора критериев. Например, технические риски зависят от критериев: сбои и поломки оборудования, неудачные испытания оборудования и др. финансовые – от макроэкономических показателей (например, инфляции), перерасход бюджета и др., временные – от задержки поставок, срывов сроков и др., организационные – от недостаточной квалификации персонала, конфликтов внутри команды и др. [20,21].
Важно учитывать данные критерии при принятии решения, но возникает сложность оценки их степени влияния. Например, как оценить степень конфликта внутри команды или ту же недостаточность квалификации? Оценить квалификацию сотрудников можно с помощью теории нечётких множеств с использованием лингвистической переменной. Лингвистическая переменная представляет собой слово или фразу, выражающую уровень какого-то качества, которое невозможно точно измерить численно и используется для описания качественных характеристик, которые трудно выразить количественно.
3. Применение лингвистической переменной для оценки уровня квалификации сотрудников
В качестве примера определим для оценки квалификации три лингвистические переменные: низкая квалификация, средняя квалификация и высокая квалификация. Каждое значение лингвистической переменной (например, низкая/средняя/высокая квалификация) должно иметь своё собственное терм-множество. Терм-множество определяет диапазон значений этой переменной, который может быть описан через функцию принадлежности, которая показывает, насколько конкретный сотрудник соответствует определённому уровню квалификации. Функция принадлежности для данной постановки задачи может выглядеть следующим образом:
Низкая квалификация: от 0 до 0,4
Средняя квалификация: от 0,3 до 0,7
Высокая квалификация: от 0,6 до 1.
Допустим, требуется оценить квалификацию трёх сотрудников: Иванов, Петров и Сидоров. Иванов имеет 10 лет опыта работы, выполнил 20 успешных проектов и получил хорошие отзывы от коллег. Петров имеет 5 лет опыта работы, выполнил 15 проектов и получил средние отзывы. Сидоров имеет 7 лет опыта работы, выполнил 18 проектов и получил отличные отзывы. Таким образом, будут определены три уровня квалификации: низкая, средняя и высокая (см. таблица 1.)
Таблица 1. Входные данные:
| Сотрудник | Опыт (лет) | Проекты | Отзывы |
| Иванов | 10 | 20 | 8 |
| Петров | 5 | 15 | 6 |
| Сидоров | 7 | 18 | 9 |
Определим диапазоны для каждого параметра:
Опыт: низкий – 0-5 лет, средний – 5-10 лет, высокий – свыше 10 лет.
Проекты: низкий – 0-10 проектов, средний – 10-20, высокий – более 20 проектов.
Отзывы: низкий – 0-5 баллов, средний – 5-8, высокий – 8-10 баллов.
Тогда функции принадлежности можно задать треугольными функциями:
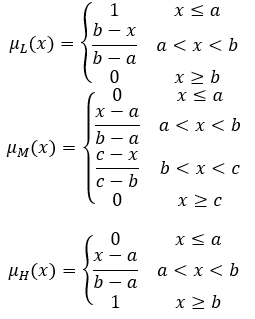 |
(1) |
где:
µL(x), µМ(x), µН(x) – функции принадлежности для низкого, среднего и высокого уровней соответственно.
a, b, c – границы диапазонов для низкого, среднего и высокого уровней соответственно.
Теперь можно найти средневзвешенное итоговое значение квалификации сотрудника:
| (2) |
где wi – весовые коэффициенты,
μi— значения функции принадлежности.
Рассчитав по этой формуле коэффициенты S, получим величины значимости каждого сотрудника.
4. Применение теории нечётких множеств для оценки рисков проекта.
Чтобы применить данную модель для оценки рисков проекта, в котором участвуют сотрудники с разной квалификацией, потребуется расширить исходную модель, добавив дополнительные параметры, связанные с рисками. В этом случае можно рассматривать квалификацию сотрудников как один из ключевых факторов риска выполнения проекта. Вначале выделим факторы, для оценки рисков:
- Затраты – риск превышения бюджета;
- Время – риск затягивания сроков;
- Технические сложности – риск недооценки сложности технических решений;
- Изменчивость требований – риск частых изменений требований.
Каждому фактору также присваиваются лингвистические переменные с соответствующими функциями принадлежности:
Затраты: низкий, средний, высокий уровень затрат.
Время: короткие, средние, длительные сроки.
Технические сложности: простая, средняя, сложная задача.
Изменчивость требований: стабильные, умеренные, частые изменения.
Тогда функция принадлежности для затрат может принять вид:
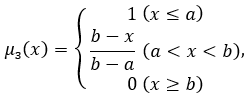 |
(3) |
где a и b – пороговые значения для низких и высоких затрат
Объединим факторы риска с учетом квалификации сотрудников:
| (4) |
где wi – весовые коэффициенты,
R3 — риск превышения затрат,
Rвр — риск превышения времени,
Rтсложн — риск технической сложности,
Rизмтр — риск изменчивости требований,
Q – квалификация команды.
Рассмотрим некоторый пример расчета.
Предположим, что затраты проекта высокие (0.8), время выполнения среднее (0.5), технические сложности низкие (0.2), требования меняются часто (0.7). Квалификация команды оценивается как высокая (0.85).
Пусть веса факторов равны:
w1=0,25; w2 =0,2; w3=0,15; w4=0,2; w5=0,2.
Тогда:
R=0,25⋅0,8+0,2⋅0,5+0,15⋅0,2+0,2⋅0,7+0,2⋅0,85=0,64
Полученный результат 0,64 интерпретируется как умеренно высокий уровень риска проекта.
Заключение
Таким образом, анализируя результаты проведённого обзора и рассмотренную модель, построенную на основе теории нечётких множеств с использованием лингвистических переменных, можно сделать ряд важных выводов.
Во-первых, традиционные методы многокритериального анализа, такие как метод взвешенной суммы и метод уступок, обладают несомненными преимуществами простоты и относительной лёгкости реализации. Однако они существенно ограничены высокой степенью субъективности при выборе весов и критериев, а также недостаточной гибкостью в условиях неопределённости и изменчивости исходных данных. Это снижает их эффективность при решении сложных задач, где параметры оценки обладают качественным характером или изменяются во времени.
Во-вторых, методы Парето-оптимизации демонстрируют высокую эффективность при работе с конфликтующими критериями, позволяя выявить множество оптимальных решений без необходимости сводить все показатели к единому числовому значению. Тем не менее, отсутствие единственного решения требует дополнительного анализа и выбора наиболее приемлемого варианта с учётом конкретных предпочтений и ограничений, что усложняет процесс принятия решений.
В-третьих, теория нечётких множеств представляется наиболее перспективным направлением, поскольку она позволяет формализовать качественные параметры, которые традиционные количественные методы не в состоянии адекватно обработать. Использование лингвистических переменных даёт возможность учитывать экспертные оценки, такие как квалификация сотрудников, уровень риска, технические сложности и другие субъективные факторы, которые часто имеют место в управлении проектами. Кроме того, данный подход позволяет учитывать динамические изменения условий (например, колебания бюджета и сроков), что значительно повышает адаптивность модели.
Предложенный в работе подход на базе теории нечётких множеств и лингвистических переменных обеспечивает эффективное учёт неопределённости и качественных характеристик, что делает его особенно актуальным для управления сложными и многогранными проектами. Вместе с тем, для успешного внедрения данной методологии необходимо проведение дополнительной адаптации моделей с учётом специфики конкретных задач и отраслей, а также проведение широких практических испытаний и апробации в реальных условиях.
Таким образом, дальнейшее развитие и совершенствование нечётких моделей с лингвистическими переменными открывает новые перспективы для повышения качества и надёжности принятия решений в условиях неопределённости и многокритериальности.
Читайте также
Библиографический список
- Есипов, Б.А. Методы исследования операций : учебное пособие. 2nd-е изд., испр. и доп. ed. Санкт-Петербург: Лань, 2022. 304 с.
- Горлач, Б.Ф. Исследование операций : учебное пособие. Санкт-Петербург: Лань, 2022. 448 с.
- Steuer, R.E. Multiple criteria optimization: theory, computation, and application. Malabar, Fla: Krieger, 1989. xx, 546 с.
- Chankong, V., Haimes Y.Y. Multiobjective Decision Making: Theory and Methodology. Dover Publications, 2008. 432 с.
- Geoffrion, A.M. Proper efficiency and the theory of vector maximization. Santa Monica, Calif: Rand Corс., 1967. 21 с.
- Подиновский, В.В., Ногин, В.Д. Парето-оптимальные решения многокритериальных задач : монография — Подиновский В.В. 2nd-е изд., испр. и доп. ed. Москва: Физматлит, 2007. 255 с.
- Лотов, А.В., Поспелова, И.И. Многокритериальные задачи принятия решений: учебное пособие. Москва: Макс-Пресс, 2008. 196 с.
- Васильев Ф.П. Методы оптимизации: учебник для студентов высших учебных заведений, обучающихся по специальности ВПО 010501 “Прикладная математика и информатика”: [в 2 кн.]. Изд. новое, перераб. и доп. Москва: Изд-во МЦНМО, 2011.
- Бродецкий, Г.Л., Гусев, Д.А., Мазунина, О.А. Системный анализ в логистике. Выбор при многих критериях: учебник: для студентов учреждений высшего образования, обучающихся по направлению подготовки “Менеджмент”, профиль “Логистика и управление цепями поставок.” Москва: Академия, 2018. 222 с.
- Казанская, О.В., Юн, С.Г., Альсова, О.К. Модели и методы оптимизации: практикум: учебное пособие. Новосибирск: НГТУ, 2012. 202 с.
- Канторович, Л.В. Экономический расчет наилучшего использования ресурсов. Москва: Изд-во Акад. наук СССР, 1959. 344 с.
- Гранберг, А.Г. Основы региональной экономики: Учеб. для вузов. 3rd-е изд ed. Москва: ГУ ВШЭ, 2003. 492 с.
- Полтерович, В.М. Элементы теории реформ. Москва: Экономика, 2007. 445 с.
- Прохоренков, П.А. Выделение множества Парето-оптимальных решений в задачах многокритериальной оптимизации и планирования оптимальных регрессионных экспериментов: диссертация … кандидата технических наук: 05.13.01. Москва, 1982. 210 с.
- Белецкая, С.Ю. Математические методы поиска оптимальных решений: учебное пособие. Воронеж: Воронежский гос. технический ун-т, 2008. 201 с.
- Лемешко, Б.Ю. Методы оптимизации: конспект лекций. Новосибирск: НГТУ, 2009. 154 с.
- Виленкин, Н.Я. Метод последовательных приближений: Пер. с рус. 2nd-е изд ed. Москва: Мир, 1983. 120 с.
- Орлов, А.И. Теория принятия решений. Москва: Ай Пи Ар Медиа. 826 с.
- Zadeh, L.A. Fuzzy sets // Information and control. Elsevier, 1965. Vol. 8, № 3. С. 338–353.
- Борисов, А.Н., Крумберг, О.А., Федоров, И.П. Принятие решений на основе нечетких моделей: Примеры использ. Рига: Зинатне, 1990. 184 с.
- Бахусова, Е.В. Элементы теории нечётких множеств: учеб.- метод. пособие. Тольятти: Издательство ТГУ, 2013. 116 с.
References
- Yesipov, B.A. Methods of Operations Research: Textbook. [Metody issledovaniya operatsiy: uchebnoe posobie]. 2nd ed., revised and enlarged. Saint Petersburg: Lan, 2022. 304 p.
- Gorlach, B.F. Operations Research: Textbook. [Issledovanie operatsiy: uchebnoe posobie]. Saint Petersburg: Lan, 2022. 448 p.
- Steuer, R.E. Multiple Criteria Optimization: Theory, Computation, and Application. Malabar, Fla: Krieger, 1989. xx, 546 p.
- Chankong, V., Haimes, Y.Y. Multiobjective Decision Making: Theory and Methodology. Dover Publications, 2008. 432 p.
- Geoffrion, A.M. Proper Efficiency and the Theory of Vector Maximization. Santa Monica, Calif: Rand Corp., 1967. 21 p.
- Podinovskiy, V.V., Nogin, V.D. Pareto-Optimal Solutions of Multicriteria Problems: Monograph. [Pareto-optimal’nye resheniya mnogokriterial’nykh zadach: monografiya]. 2nd ed., revised and enlarged. Moscow: Fizmatlit, 2007. 255 p.
- Lotov, A.V., Pospelova, I.I. Multicriteria Decision Making Problems: Textbook. [Mnogokriterial’nye zadachi prinyatiya resheniy: uchebnoe posobie]. Moscow: Max-Press, 2008. 196 p.
- Vasiliev, F.P. Optimization Methods: Textbook for Students of Higher Education Institutions, Specialty VPO 010501 «Applied Mathematics and Informatics»: [in 2 vols.]. New edition, revised and enlarged. Moscow: MCNMO Publishing, 2011.
- Brodetskiy, G.L., Gusev, D.A., Mazunina, O.A. Systems Analysis in Logistics. Choice Under Multiple Criteria: Textbook for Students of Higher Education Institutions, Major «Management», Profile «Logistics and Supply Chain Management.» Moscow: Akademiya, 2018. 222 p.
- Kazanskaya, O.V., Yun, S.G., Alsova, O.K. Models and Optimization Methods: Practical Course: Textbook. [Modeli i metody optimizatsii: praktikum: uchebnoe posobie]. Novosibirsk: NSTU, 2012. 202 p.
- Kantorovich, L.V. Economic Calculation of the Best Use of Resources. [Ekonomicheskiy raschet nailuchshego ispol’zovaniya resursov]. Moscow: Publishing House of the Academy of Sciences of the USSR, 1959. 344 p.
- Granberg, A.G. Fundamentals of Regional Economics: Textbook for Universities. [Osnovy regional’noy ekonomiki: ucheb. dlya vuzov]. 3rd ed. Moscow: HSE, 2003. 492 p.
- Polterovich, V.M. Elements of Reform Theory. [Elementy teorii reform]. Moscow: Ekonomika, 2007. 445 p.
- Prokhorenkov, P.A. Identification of the Set of Pareto-Optimal Solutions in Multicriteria Optimization Problems and Planning of Optimal Regression Experiments: Candidate of Technical Sciences Dissertation: 05.13.01. [Vydelenie mnozhestva Pareto-optimal’nykh resheniy v zadachakh mnogokriterial’noy optimizatsii i planirovaniya optimal’nykh regressivnykh eksperimentov: dissertatsiya … kandidata tekhnicheskikh nauk]. Moscow, 1982. 210 p.
- Beletskaya, S.Yu. Mathematical Methods for Searching Optimal Solutions: Textbook. [Matematicheskie metody poiska optimal’nykh resheniy: uchebnoe posobie]. Voronezh: Voronezh State Technical University, 2008. 201 p.
- Lemeshko, B.Yu. Optimization Methods: Lecture Notes. [Metody optimizatsii: konspekt lektsiy]. Novosibirsk: NSTU, 2009. 154 p.
- Vilenkin, N.Ya. Method of Successive Approximations: Translation from Russian. [Metod posledovatel’nykh priblizheniy: Per. s rus.]. 2nd ed. Moscow: Mir, 1983. 120 p.
- Orlov, A.I. Decision Theory. [Teoriya prinyatiya resheniy]. Moscow: IP AR Media, 826 p.
- Zadeh, L.A. Fuzzy Sets // Information and Control. Elsevier, 1965. Vol. 8, No. 3. P. 338–353.
- Borisov, A.N., Krumberg, O.A., Fedorov, I.P. Decision Making Based on Fuzzy Models: Examples of Use. [Prinyatie resheniy na osnove nechetkikh modeley: primery ispol’zovaniya]. Riga: Zinatne, 1990. 184 p.
- Bakhusova, E.V. Elements of Fuzzy Set Theory: Teaching and Methodological Manual. [Elementy teorii nechetkikh mnozhestv: ucheb.-metod. posobie]. Tolyatti: TGU Publishing, 2013. 116 p.





