Оптимизация контроля управления качеством производства
Optimizing control of quality management

Авторы
Аннотация
Статья содержит описание технологии, позволяющей осуществлять контроллинг бизнес-процессов на промышленных предприятиях. Приведен пример использования контрольной карты как одного из эффективных статистических методов контроля качества выпускаемой продукции. Автором дано определение, наиболее полно раскрывающее понимание качества и контроля качества.
Ключевые слова
моделирование бизнес-процессов, контрольная карта, корреляционный анализ в моделировании процессов.
Рекомендуемая ссылка
Флигинских Татьяна Николаевна, Федорец Ксения Сергеевна. Оптимизация контроля управления качеством производства // Современные технологии управления. ISSN 2226-9339. — №5 (17). Номер статьи: 1705. Дата публикации: 08.05.2012. Режим доступа: https://sovman.ru/article/1705/
Authors
Abstract
This paper describes the technology that permits controlling of business processes in industry. An example of the use of control charts as one of the most effective methods of statistical quality control of products. The author provides a definition that best reveals the understanding of quality and quality control.
Keywords
business process modeling, control chart, correlation analysis in the modeling process.
Suggested citation
Fliginskih Tatyana Nikolayevna, Fedoretc Ksenia Sergeevna. Optimizing control of quality management // Modern Management Technology. ISSN 2226-9339. — №5 (17). Art. # 1705. Date issued: 08.05.2012. Available at: https://sovman.ru/article/1705/
Основной задачей методов контроля является обеспечение производства пригодной к употреблению продукции и оказание полезных услуг с наименьшими затратами. Одним из основных принципов контроля качества при помощи статистических методов является стремление повысить качество продукции, осуществляя контроль на различных этапах производственного процесса. Применение контрольных методов – весьма действенный путь разработки новой технологии и контроля качества производственных процессов. Контроль можно так же осуществлять с помощью математического моделирования бизнес – процесс, математический анализ позволяет сопоставить статистические данные и определить оптимальные показатели развития системы.
Любой производственный процесс представляет собой совокупность входных параметров, таких как свойств исходного сырья, точности технологического и контрольного оборудования, квалификации персонала и другие. Эти параметры могут испытывать колебания двух типов: случайные, которые возникают спонтанно и не могут быть устранены, и неслучайные, которые возникают систематически в течение производственного процесса и могут быть либо устранены, либо сведены к минимуму.
Результатом этих колебаний является разброс уровня качества производственного процесса. Если колебания входных параметров носят только случайный характер, то процесс будет считаться налаженным. Пределы качества процесса называют его естественными границами и рассматриваются как мера его технических возможностей. При неслучайном характере колебаний процесса уровень его качества может выйти за естественные границы. Это означает, что существуют факторы, допускающие изучение. Чтобы управлять процессом, к этим причинам нужно вернуться.
Для наглядного отображения производственного процесса, и своевременного распознавания его отклонений от заданных норм построим контрольную карту на основе методологии Вальтера Шухарта качественного оперативного планирования деятельности хозяйствующего субъекта. Контрольная карта представляет собой графическую зависимость показателей контролируемого параметра во времени. Контрольная карта – это разновидность графика, однако, в отличие от обычного графика на контрольную карту наносят контрольные значения, которые называются границами регулирования. Эти контрольные значения обозначают ширину разброса данных, образующегося в обычных условиях течения процесса, т.е. определяют его естественные границы. Контрольная карта позволяет следить за состоянием процесса во времени, и более того, воздействовать на этот процесс до того, как он выйдет из-под контроля. Если все точки, представляющие состояние процесса на контрольной карте, входят в область, ограниченную контрольными границами, это указывает на то, что процесс протекает в относительно постоянных условиях, т.е. процесс стабилен и находится в контролируемом состоянии.
Если значение показателя вышло за эти границы, то возможны два случая:
а) выпадающее значение – это значение, относящееся к генеральной совокупности, но выходящее за границы регулирования. В этом случае в технологический процесс вмешиваться не рекомендуется;
б) при изменении входных параметров (режима, исходного сырья, оборудования) значение показателя может выйти за границы регулирования. Следовательно, выпадающее значение относится к другой генеральной совокупности и выход за границы регулирования не случаен. В этом случае необходимо исследовать причину нарушения технологического процесса и устранить ее. Если значение выходит за границы регулирования, а предыдущие значения показателя качества находятся довольно близко к границе регулирования, то вполне вероятно, что процесс протекает с систематическими отклонениями. Если предыдущие значения беспорядочно рассеяны между верхней и нижней границами регулирования, то отклонение будет случайным.
В порядке составления контрольной карты самым важным является способ определения контрольных границ. Для определения контрольных границ (или контрольных нормативов) необходимо собрать большое количество данных, называемых предварительными данными, характеризующими состояние процесса, и на их основе рассчитать по установленной формуле контрольные нормативы.
В производственной практике используют несколько видов контрольных карт, отличающихся друг от друга характером используемых данных. Если показатели качества могут быть выражены количественными данными – размеры, вес, твердость и т.д., то используют так называемые контрольные карты по количественному признаку. В тех случаях, когда показатели качества определяются качественными данными, типа «качественно» и «некачественно» используют контрольные карты по альтернативному признаку.
Применению контрольных карт должен предшествовать предварительный статистический анализ процесса и устранение выявленных недостатков. Без этого внедрение контрольных карт не имеет смысла. В случае, когда данные о процессе поступают через большие интервалы времени или само группирование данных не эффективно составляется карта индивидуальных значений. Данные наносятся на график отдельными точками по мере поступления, и их используют для построения контрольной карты.
При составлении карты индивидуальных значений в качестве характеристики процесса используются отдельные значения – индивидуальные значения выборки. Каждое из значений выборки сравнивается с определенной областью допустимых значений, по выходу какого-либо значения за границы этой области судят о поведении процесса и необходимости подналадки. Если, например, в выборке из пяти деталей размеры хотя бы двух вышли за контрольные границы, т.е. за верхний или нижний пределы поля допуска, то подается сигнал о разналадке процесса.
В таблице 1 приведены основные формулы для расчета контрольных линий для контрольных карт по количественному и альтернативному признакам. Далее в стандарте будет рассмотрено подробное применение приводимых в таблице 2 формул по всем видам контрольных карт.
Таблица 1 — Основные формулы расчета контрольных линий
| Вид контрольной карты | Верхний контрольный предел (UCL), центральная линия (CL), нижний контрольный предел (LCL) |
| Xкр | UCL = Xкр2 = Xmax + rmax, CL =Xкр LCL = Xкр1 =Xmin + rmin |
| Xmed | UCL = Xmed+ 3,76 / √N * δ CL = Xmed LCL = Xmed- 3,76 / √N* δ |
| X | UCL = CL = X LCL = |
| R | UCL = D4 R CL = R LCL = D3 R |
| δ | UCL = δ√N/ 1 CL = δ LCL = δ√N/ 2 |
| р | UCL = p+ 3 √ P(1-P) / n CL = p LCL = p- 3 √ P(1-P) / n |
| n | UCL = pn + 3 √ Pn(1-P) CL = pn= nΣpn / Σn, LCL = pn — 3 √ Pn(1-P) |
| с | UCL = C + 3 √C CL =C LCL = C — 3 √C |
| u | UCL = U+ 3√ U / n CL = U LCL = U- 3√ U / n |
Все методы, использующие отдельные значения в выборке, должны базироваться на малых объемах выборок. Регулирование по одному изделию также можно рассматривать как пример применения одного из этих методов.
Самым перспективным из методов, использующих индивидуальные значения, является метод крайних значений. После упорядочения данных, крайние члены, то есть максимальное и минимальное значения в выборке, сравниваются с соответствующими контрольными областями и при выходе какого-либо из крайних членов за контрольные границы, дается сигнал на подналадку или остановку процесса. Контрольные границы определяются соответственно для наибольшего и наименьшего значений следующим образом:
для наименьшего значения Xкр1 =Xmin + rmin; (1)
для наибольшего значения Xкр2 = Xmax + rmax, (2)
где Xmin и Xmax – средние значения из наименьших и наибольших значений;
rmin и rmax половина разности между самым большим и самым малым среди наименьших и наибольших значений в тех же выборках.
На бланке контрольной карты по вертикальной оси откладывают значения х, а по горизонтальной оси – номера групп. На график наносят контрольные границы, обозначающиеся обычно пунктирной линией и центральную линию (сплошную). В заключение наносят точками значения х для каждой группы.
На контрольной карте должны указываться: объем выборки n, значения центральных линий, а также значения верхних и нижних пределов, название процесса и продукта, период времени, метод измерения, условия работы, смена и т.д.
Таблица 2 — Исходные данные для построения хкр – карты
| Номер группы |
Х1 | Х2 | Х3 | Х4 | Х5 | Хmax | Хmin | Х |
| 1 2 3 4 5 |
47 19 19 29 28 |
32 37 11 29 12 |
44 31 16 42 45 |
35 25 11 59 36 |
20 34 44 38 25 |
47 37 44 59 45 |
20 19 11 29 12 |
178 146 101 197 146 |
| Итого | 59 | 11 | 868 | |||||
| Среднее Xmax = 46,4 Xmin = 18,2 | ||||||||
Определим максимальное и минимальное значение в каждой группе. Для вычисления общего среднего значения из максимальных итогов столбца xmax необходимо разделить на число групп:
Xmax = (xmax1+ xmax2+…. + xmax3) / k, (3)
где k — число групп.
Аналогично рассчитывается и общее среднее значение из инимальных:
Xmin = (xmin1 + xmin2 + …..+ xmin3) / k (4)
Из полученных минимальных и максимальных значений в строках таблицы 2 выбираем самое большое и самое маленькое из максимумов и минимумов. Самым большим из максимумов будет х = 59, а из минимумов х = 29. Самым маленьким из максимумов будет х=37, а из минимумов х=11. Рассчитаем rmin и rmax: rmin = (59 – 37) / 2 = 11; rmax = (29 – 11) / 2 = 9.
Тогда для рассматриваемого примера верхний контрольный предел находим по формуле 2:
Xкр2 = 46,4 + 11 = 57,4
Нижний контрольный предел находим по формуле 1:
Xкр1 = 18,2 + 9 = 27,2
На контрольную карту нанесем контрольные границы, а также значения х для каждой группы. Необходимо определить, все ли точки находятся внутри границ регулирования, и сделать соответствующее заключение о стабильности данного технологического процесса. Верхние и нижние пределы контрольной карты определяются:
Хmed – карта:
Центральная линия CL = Xmed
Верхний контрольный предел
UCL (Upper control level) = Xmed+ 3√ / 2n* δ
или после преобразования UCL = Xmed+ 3,76 / √N* δ
Нижний контрольный предел
LCL (Lower control level) = Xmed- 3,76 / √N*δ,
где δ- оценка параметра генеральной совокупности.
Оценку параметра δ определим при помощи размаха R.
δ = R/ d,
где d – коэффициент, зависящий от объема выборки n. Значение коэффициента d приведены в таблице 3
Таблица 3 – Статистические и математические данные Контрольной карты
| Объем подгруппы, n |
X-карта | R-карты | ||
| A2 | D3 | D4 | d | |
| 1 2 3 4 5 6 7 8 9 |
1,880 1,023 0,729 0,577 0,483 0,419 0,373 0,337 0,308 |
— — — — — 0,076 0,136 0,184 0,223 |
3,267 2,575 2,282 2,115 2,004 1,924 1,864 1,816 1,777 |
1,128 1,693 2,059 2,326 2,534 2,704 2,847 2,970 3,078 |
Все точки, представляющие состояние процесса на контрольной карте, входят в область, ограниченную контрольными границами, это указывает на то, что процесс протекает в относительно постоянных условиях, т.е. процесс стабилен и находится в контролируемом состоянии (рис. 1).
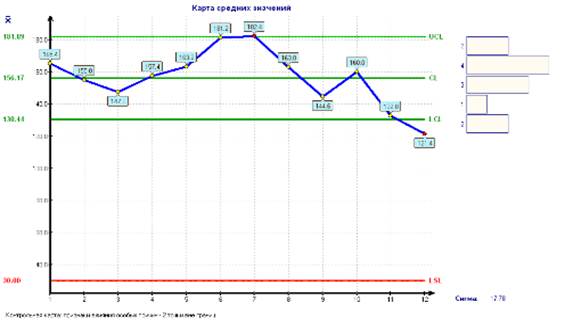
Рис.1. Контрольная карта
Таким образом, на основании разработанной концепция оперативного — планирования деятельности предприятия, возможно, проанализировать и оценить решение основных стратегических задач деятельности финансово-экономического блока, что наряду с совершенствованием системы управленческого учета позволит существенно повысить эффективность ее функционирования. Разработать и реализовать программу «Развитие предприятия на основе концепции ограниченного роста, базирующегося на принципе развития с минимальными рисками достигнутого». А так же для анализа эффективности финансовой и маркетинговой деятельности проводимой на предприятие необходимой для оценки структуры экспорта и внутреннего рынка. Все точки находятся внутри границ регулирования, что свидетельствует о стабильности данного технологического процесса.
К недостаткам контрольных карт по количественным признакам следует отнести то, что каждая карта позволяет контролировать только один признак изделия, в то время как качество большинства изделий определяется по нескольким признакам. В этом случае на практике приходится выбирать для контроля один или два основных признака. Этого недостатка лишены контрольные карты по альтернативным признакам. Преимущество таких карт заключается в том, что с помощью одной карты можно контролировать несколько признаков изделия, подсчитывая количество имеющихся в нем дефектов. Эффективность контрольных карт по альтернативным признакам несколько ниже количественных.
Читайте также
Библиографический список
- Уилер Д. Статистическое управление процессами. Оптимизация бизнеса с использованием контрольных карт Шухарта. М.: Альпина Бизнес Букс, 2009. 410с.
- Фалько С.Г. Контроллинг для руководителей и специалистов. – М.: Финансы и статистика, 2008. – 272 с.:ил.
- Елиферов В.Г. Бизнес-процессы. Регламентация и управление. М.: Инфра — М; Синергия, 2009. 318с.
- Прохоров Ю.К.Управление качеством: учебное пособие. – СПб: СПбГУИТМО, 2007.
References
- Wheeler, D. Statistical Process Control. Business Optimization using Shewhart control charts. MA: Harvard Business Review, 2009. 410C.
- Falko S.G. Controlling for managers and professionals. – Moscow: Finances and Statistics, 2008. – 272 p. Ill.
- Eliferov V.G. Business processes. The regulation and control. Moscow: Infra – M, Synergy, 2009. 318s.
- Prokhorov, J.K. Quality management: a training manual. – St. Petersburg: SPbGUITMO, 2007.