Разработка системы обслуживания станков на производстве
Development of machine interference system in industries

Авторы
Аннотация
Целью работы является повышение эффективности управления гибким производственным участком, путем решения задачи оптимального распределения трудовых ресурсов. В результате работы был создан критерий оптимальности, который позволяет охарактеризовать работу исследуемой системы и выбрать наилучший вариант её организации, при котором выпуск продукции будет максимальным. Основные разделы работы: 1) основные направления теории массового обслуживания при анализе производственных процессов; 2) критерий оптимальности в производственной задаче массового обслуживания; 3) определение оптимального числа операторов-наладчиков в цехе.
Ключевые слова
система массового обслуживания, источник требований, входящий поток требований, очередь, обслуживающие устройства (каналы обслуживания), выходящий поток требований, критерий оптимальности, коэфициент сезонности, коэффициент простоя рабочих мест, среднее число требований, находящихся в системе, коэффициент нахождения рабочих мест вне системы обслуживания, вероятность того, что все обслуживающие аппараты свободны.
Рекомендуемая ссылка
Родина Вероника Игоревна. Разработка системы обслуживания станков на производстве // Современные технологии управления. ISSN 2226-9339. — №9 (33). Номер статьи: 3307. Дата публикации: 08.09.2013. Режим доступа: https://sovman.ru/article/3307/
Authors
Abstract
The aim of this work is to improve the control effectiveness of cell-type system due to solving the problem of optimal allocation of labor force. An optimality criterion was created as a result of this work. It allows to characterize the operation of the system and choose the best option of its organization which has maximized output. The main sections of the work: 1) The main directions of queuing theory in the analysis of production processes; 2) Optimality criterion in the production task of queuing; 3) Determination of the optimal number of operators in production units.
Keywords
service system, input sours, input customer flow, queue, queuers(service lines), output customer flow, optimality criterion, seasonality factor, coefficient of loss of working places, average number of customer flows in a system, coefficient of finding working places outside the service system, the probability that all service machines are free.
Suggested citation
Rodina Veronika Igorevna. Development of machine interference system in industries // Modern Management Technology. ISSN 2226-9339. — №9 (33). Art. # 3307. Date issued: 08.09.2013. Available at: https://sovman.ru/article/3307/
Введение
Многие экономические задачи, в том числе и задачи рынка труда, связаны c системами массового обслуживания, т.е. такими системами, в которых, с одной стороны, возникают массовые запросы (требования) на выполнение каких-либо услуг, с другой – происходит удовлетворение этих запросов. Система массового обслуживания включает в себя следующие элементы: источник требований, входящий поток требований, очередь, обслуживающие устройства (каналы обслуживания), выходящий поток требований. Исследованием таких систем занимается теория массового обслуживания [1].
1. Основные направления теории массового обслуживания при анализе производственных процессов
Основным местом применения теории массового обслуживания в исследованиях по повышению эффективности производства является определение оптимальных вариантов организации работы вспомогательных служб и хозяйств, обеспечивающих бесперебойную работу технологического оборудования в цехах и на участках основного производства.
Факторами, влияющими на качество обслуживания в производственных системах массового обслуживания, будут численность обслуживающих аппаратов, численность источников, посылающих требования, расходы на содержание аппаратов, выпуск продукции источниками требований и т. п [1].
В данной работе в качестве экономического объекта исследования принят гибкий производственный участок, который состоит из станков-автоматов с высокой степенью гибкости, обслуживаемых операторами и наладчиками, управляемых мастерами и наладчиком участка, которые связаны между собой в том или другом смысле. Под потоком требований понимается поток заявок на обслуживание станков. Под временем обслуживания понимается среднее время обслуживания одного станка. Источником, посылающим требование в систему, является человек, работающий на станке. Обслуживающим аппаратом в системе является оператор-наладчик станка.
Цель исследования заключается в повышении эффективности программного управления гибким производственным участком путем математического моделирования его функционирования с использованием математического аппарата теории массового обслуживания.
Предметом исследования являются математическое описание и оптимальная организация функционирования гибкого производственного участка.
В нашей работе будем рассматривать систему массового обслуживания со следующими характеристиками:
- условия производства в основных цехах машиностроения чаще всего таковы, что производственный процесс не может продолжаться, пока рабочее место не получит требуемых услуг (оборудование не может работать, если оно не отремонтировано), поэтому осуществление операций обслуживания похоже на функционирование систем массового обслуживания с ожиданием;
- число рабочих мест и число единиц машин и оборудования, от которых поступают требования на обслуживание, в основных цехах всегда является ограниченным и поддается более или менее точному учету, поэтому потоки требований следует считать чаще всего ограниченными;
- число обслуживающих аппаратов в формулированной модели массового обслуживания конечное;
- условия обслуживания на производстве чаще всего являются такими, что к обслуживанию поступившего требования может приступить любой свободный аппарат, потому встречающиеся на производстве модели будут иметь неупорядоченный характер обслуживания;
- Поток требований является случайной величиной и описывается показательным законом распределения с параметром λ . Время обслуживания заявки является случайной величиной и описывается показательным законом распределения с параметром ν[1].
2. Критерий оптимальности в производственной задаче массового обслуживания
Теория массового обслуживания, разрабатывая модели различных cистем выводит формулы, по которым могут быть рассчитаны лишь общие характеристики функционирования систем, и не указывает на то, какая из характеристик должна быть определяющей и какой из вариантов организации системы следует выбирать в качестве оптимального. Оптимальность же зависит от принятого критерия оптимальности, т.е. от главного изменяющегося показателя работы системы [2].
Одним из критериев оптимальности может быть максимальный выпуск продукции обслуживающими рабочими единицами основного производства в цехе:
![]() [1],
[1],
где uo= (1-u)- коэффициент нахождения рабочих мест вне системы обслуживания.
B – возможный объем выпуска продукции при изменении численности аппаратов обслуживающей системы (операторов-наладчиков) до r, при котором и коэффициент простоев основных рабочих мест изменяется соответственно до u;
Bo – объем выпуска продукции при существующей во время исследований численности (ro) обслуживающей системы в цехе;
uo- коэффициент простоя рабочих мест при определенном количественном составе системы;
u — коэффициент простоя рабочих мест при изменяющемся количественном составе системы.
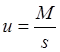 ,
,
где s – наибольшее возможное число требований, находящихся в обслуживающей системе одновременно;
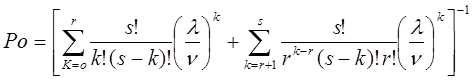
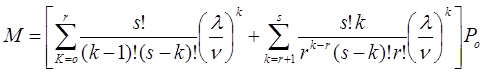
— среднее число требований, находящихся в обслуживающей системе[1],
где
— вероятность того, что все обслуживающие аппараты свободны [1],
r– количество наладчиков в цехе,
λ, ν – параметры показательного закона распределения.
Обслуживающие системы влияют на величину выпуска , так как от качества обслуживания зависит величина простоев рабочих мест. При малой численности рабочих в обслуживающих системах они не смогут обслужить все заявки, если их скопиться большое количество. А поскольку требования на обслуживание поступают нерегулярно, то случаи скопления большого числа требований вполне вероятны. При этом образуются очередь стоящих в ожидании обслуживания рабочих единиц основного процесса, и цех понесет значительные потери от увеличения простоев.
В нашей работе предлагается включить в модель параметр μ, который будет являться коэффициентом, характеризующем сезонность работы. Включение данного коэффициента позволит рассчитывать выпуск продукции в соответствии с сезонными колебаниями работы, что сделает более точным расчет критерия оптимальности.
Критерий оптимальности будет выглядеть следующим образом: ![]() ,
,
где μ – коэффициент сезонности, прогнозируемый для анализируемого периода.
Произведем расчет коэффициента сезонности с помощью анализа временных рядов. Расчитаем коэффициент сезонности, очищенный от роста (табл.1).
Таблица 1
Расчет коэффициента сезонности
| Год | Месяц |
Выпуск нормо-час. |
X |
1. Значения тренда |
2. Отклонение фактических значений от значений тренда |
3. Среднее отклонение для каждого месяца |
|
2010 |
Jan. |
2030 |
1 |
3,193 |
0,635809988 |
0,71907268 |
| Febr. |
2900 |
2 |
3,211 |
0,903234737 |
0,88240826 |
|
| March |
3810 |
3 |
3,229 |
1,180082694 |
1,11029591 |
|
| April |
3880 |
4 |
3,246 |
1,195136142 |
1,08082103 |
|
| May |
3200 |
5 |
3,264 |
0,980272979 |
0,97781039 |
|
| June |
3510 |
6 |
3,282 |
1,06937157 |
1,06767715 |
|
| July |
3090 |
7 |
3,300 |
0,936305089 |
0,97011160 |
|
| Aug. |
3100 |
8 |
3,318 |
0,934266484 |
0,97858083 |
|
| Sept. |
3790 |
9 |
3,336 |
1,136085721 |
1,05486230 |
|
| Oct. |
3870 |
10 |
3,354 |
1,153873458 |
1,03636769 |
|
| Nov. |
3760 |
11 |
3,372 |
1,115122985 |
0,97099273 |
|
| Dec. |
4500 |
12 |
3,390 |
1,327539299 |
1,15177789 |
|
|
2011 |
Jan. |
1930 |
13 |
3,408 |
0,566375226 |
4. Общий индекс |
| Febr. |
3000 |
14 |
3,426 |
0,875774412 |
Сезонности |
|
| March |
3610 |
15 |
3,443 |
1,048368881 |
1,00006487 |
|
| April |
3980 |
16 |
3,461 |
1,149840644 |
||
| May |
3420 |
17 |
3,479 |
0,982969347 |
||
| June |
3600 |
18 |
3,497 |
1,029407092 |
||
| July |
3080 |
19 |
3,515 |
0,876228838 |
||
| Aug. |
3200 |
20 |
3,533 |
0,905753964 |
||
| Sept. |
3990 |
21 |
3,551 |
1,12366733 |
5. Коэффициент |
|
| Oct. |
3770 |
22 |
3,569 |
1,056384072 |
сезонности |
|
| Nov. |
3790 |
23 |
3,587 |
1,056686773 |
очищенный |
|
| Dec. |
4320 |
24 |
3,605 |
1,198472845 |
от роста |
|
|
2012 |
Jan. |
2290 |
25 |
3,622 |
0,632161495 |
0,72 |
| Febr. |
2890 |
26 |
3,640 |
0,793869498 |
0,88 |
|
| March |
3900 |
27 |
3,658 |
1,066068477 |
1,11 |
|
| April |
3780 |
28 |
3,676 |
1,028233902 |
1,08 |
|
| May |
3200 |
29 |
3,694 |
0,866243571 |
0,98 |
|
| June |
3580 |
30 |
3,712 |
0,964435531 |
1,07 |
|
| July |
3920 |
31 |
3,730 |
1,0509607 |
0,97 |
|
| Aug. |
3670 |
32 |
3,748 |
0,979234519 |
0,98 |
|
| Sept. |
3990 |
33 |
3,766 |
1,059555473 |
1,05 |
|
| Oct. |
3880 |
34 |
3,784 |
1,025468916 |
1,04 |
|
| Nov. |
3690 |
35 |
3,802 |
0,97065934 |
0,97 |
|
| Dec. |
4300 |
36 |
3,819 |
1,125818182 |
1,15 |
График изменения коэффициентом сезонности приведен на рис. 1
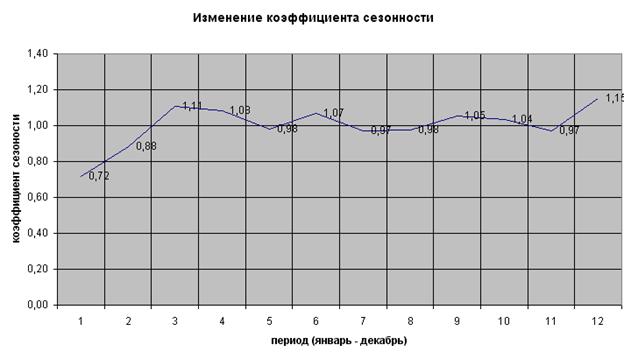
Рисунок 1 –Изменение коэффициента сезонности,
очищенного от роста по месяцам
На графике (рис.1) можно увидеть, что в марте и декабре наблюдается резкое увеличение работы. В данные периоды можно привлекать дополнительную рабочую силу: молодежь, которая только что получила образование по специальностям слесарь-ремонтик, токарь, фрезеровщик и др. и студентов для прохождения практики. Одним из механизмов привлечения выпускников является достойная оплата труда, а также поддержка в виде 40% от зарплаты в первые полгода работы.
3. Определение оптимального числа операторов-наладчиков в цехе
В нашей работе рассматривается производственный участок инструментального цеха, который имеет r=4 наладчиков, обслуживающих s=53 станков. Поток требований пуассоновский, и среднее число вызовов в течение часа составляет λ=2 ст./ч. Обслуживание одного станка является случайной величиной, распределенной по экспоненциальному закону, и среднее время одного обслуживания составляет tоб.= 30 мин. Выпуск продукции цехом в декабре 2012 года составил Bo = 4300 нормо-час. Определим основные характеристики системы и, используя критерий оптимальности, оптимальное число наладчиков, при котором выпуск продукции будет максимальным.
Таблица 2
Расчет выпуска продукции при изменении r – численности обслуживающей системы на декабрь 2012г.
|
|
r=1 |
r=2 |
r=3 |
r=4 |
r=5 |
|
uo |
0,9621 |
0,96760 |
0,97605 |
0,97695 |
0,97750 |
|
u |
0,03790 |
0,03240 |
0,02395 |
0,02305 |
0,02250 |
|
M |
1,98678 |
1,71737 |
1,26947 |
1,22167 |
1,19126 |
|
s |
53 |
53 |
53 |
53 |
53 |
|
Bo |
4300 |
4300 |
4300 |
4300 |
4300 |
|
μ |
1,15 |
1,15 |
1,15 |
1,15 |
1,15 |
|
B |
4897 |
4932 |
4942 |
4945 |
4945 |
В таблице 2 приведен расчет следующих характеристик ситстемы: uo –коэффициент нахождения рабочих мест вне системы обслуживания; u — коэффициент простоя рабочих мест; М- среднее число требований, находящихся в обслуживающей системе; Po – вероятность того, что все обслуживающие аппараты свободны; Pk – вероятность того, что занято k обслуживающих аппаратов; B — выпуск продукции с учетом коррекции на коэффициент сезонности.
В таблице 2 известны следующие данные: s– количество станков в цехе в исследуемый период; Bo — объем выпуска продукции при существующей во время исследований численности обслуживающей системы в цехе; μ– коэффициент сезонности в исследуемом периоде.
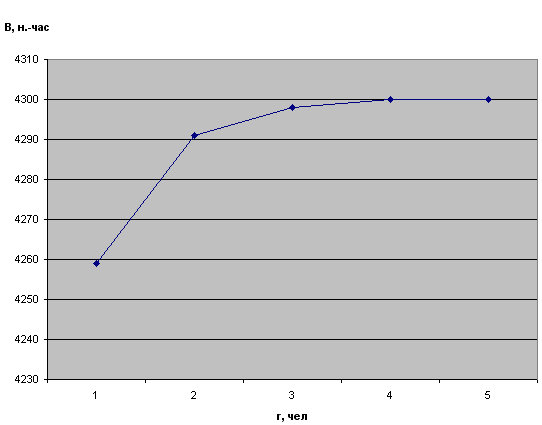
Рисунок 2 – Изменение выпуска продукции для различных вариантов организации системы с учетом коэффициента сезонности
По графику на рис.2 видно, что максимизация критерия оптимальности достигается при r= 4 . Следовательно, количество операторов-наладчиков не следует изменять. При уменьшении r возможны потери в выпуске продукции, а при увеличении r выпуск продукции не изменен, но при таком варианте возникают издержки, связанные с содержанием дополнительных единиц труда.
Заключение
Включение коэффициента сезонности в выбранный критерий оптимальности является целесообразным, поскольку полученные расчеты наиболее полно отражают ситуация для конкретного периода.
Расчет коэффициента сезонности позволит:
1) Скорректировать прогноз выпуска продукции с учетом сезонности
2) Выбрать время для активного стимулирования работы, проведения соответствующих мероприятий
3)Определить приоритеты по месяцам в рамках года.
Решение задачи оптимального распределения трудовых ресурсов приводит к ликвидации внутрисменных простоев рабочих и оборудования, повышению ритмичности производства, росту производительности труда, увеличению выпуска продукции и снижению её себестоимости. Таким образом, теория массового обслуживания позволила охарактеризовать работу исследуемой системы, рассмотреть различные варианты её организации и показатели качества обслуживания основного производства при этих вариантах и выбрать наилучший с точки зрения принятого критерия условия согласования производства в данном цехе [3].
Читайте также
Библиографический список
- Алдохин И.П. Теория массового обслуживания в промышленности. – М.: Экономика, 1970. -207с.
- Комаров А.В. Определение оптимального числа ремонтного персонала на машиностроительном предприятии // Известия Тульского государственного университета. Серия «Технологическая системотехника». Выпуск 5. Тула: ТулГУ, 2006. — С 140 — 149.
- Митин В.М. Анализ и оптимизация систем многостаночного обслуживания в автоматизированном машиностроительном производстве. Диссертация на соиск. уч. ст. к.т.н. Тула, 1997. 178 с.
References
- Aldokhin I.P. Queuing theory in the industry [Teoriia massovogo obsluzhivaniia v promyshlennosti]. Moscow: Economics, 1970.207p.
- Komarov A.V. Determination of the optimal number of maintenance personnel at an engineering company [Opredelenie optimalnogo chisla remontnogo personala na mashinostroitelnom predpriiatii]. Izvestiya of the Tula State University. “Technological systems engineering.” issue № 5.Tula: Tula State University, 2006. p. 140-149.
- Mitin V.M. Analysis and optimization of systems of multi machine-tools service in automated machinery production [Analiz i optimizatciia sistem mnogostanochnogo obsluzhivaniia v avtomatizirovannom mashinostroitelnom proizvodstve]. Ph.D. thesis in Engineering Science. Tula, 1997. 178p.






