Метод сравнения потенциалов национальных экономик
The method of comparing the potential of national economies
Авторы
Аннотация
Получено уравнение скорости развития производственных факторов. На базе уравнения строиться индекс, который назван экономическим числом. Моделирование экономического числа основывается на статистических данных по основным факторам производства США и России. Исследуется связь экономического числа с валовым продуктом национальной экономики. Предлагается правило сравнения экономик.
Ключевые слова
экономическое число, фактор производства, влияние экономической среды, инвестиции.
Рекомендуемая ссылка
Кузнецов Сергей Борисович. Метод сравнения потенциалов национальных экономик // Современные технологии управления. ISSN 2226-9339. — №6 (54). Номер статьи: 5406. Дата публикации: 08.06.2015. Режим доступа: https://sovman.ru/article/5406/
Authors
Abstract
The equations of the rate development of the factors of production was obtained. The new index is obtained on the basis of the equations, which is called the economic number. Statistical data on the basic factors of production of national economies the US and Russia are used to calculate the economic numbers. It is proved that the economic number is not accidental. The rule is proposed for comparing national economies.
Keywords
economic number, factor of manufacture, influence of the economic environment, investment.
Suggested citation
Kuznecov Sergej Borisovich. The method of comparing the potential of national economies // Modern Management Technology. ISSN 2226-9339. — №6 (54). Art. # 5406. Date issued: 08.06.2015. Available at: https://sovman.ru/article/5406/
В теории капитала и инвестиций и в новой теории роста ведущая роль в развитии отдается инвестициям в основной капитал, знаниям и человеческому капиталу. Вопросы связи инвестиций и факторов производства обсуждались в работах Копленда (Copeland 1937), Тинберга (Tinberen 1942), Стиглера (Stigler 1947). Окончательное развитие их идей было получено в модели Солоу (Solow 1957). Дальнейшее развитие модели Солоу представлено в работах Грилихиса (Griliches 1963), Денисона (Denison 1962, 1974), в которых обсуждалось качество трудовых затрат. В последние годы прошлого столетия интенсивно разрабатывались модели учитывающие «уровень знаний» Адамc (Adams 1990), Абрамовиц (Abromovitz 1993).
Во всех этих работах не затрагиваются вопросы, связанные с недоразвитием факторов производства из-за потери или пустой траты инвестиций в связи с негативными явлениями в экономике или/и политике государства. Такие явления названы экономическим сопротивлением среды.
В работе получено векторное уравнение, описывающее связь инвестиций с факторами производства и учитывающее экономическое сопротивление среды.
Будем рассматривать модель, в которой рост производственных факторов осуществляется за счет инвестиций, а банковская и налоговая политика учитываются посредством коэффициентов сопротивления экономической среды.
Рассмотрим некоторый непрерывный векторный экономический показатель 
, где 
, t — время, L — трудовые ресурсы, K — физический капитали Н — человеческий капитал. В работе в качестве такого показателя будет рассмотрен вектор скорости изменения производственных факторов. Величина 
представляет собой эту скорость.
Выберем в пространстве факторов производства Ω некоторую точку с координатами . Вокруг этой точки опишем некоторый замкнутый контур С, который стягивает поверхность S1. На полученной поверхности располагаются начальные условия, описывающие состояние экономических объектов. В замкнутом контуре С разброс в объеме факторов производства небольшой и позволяющий утверждать, что скачки в развитии факторов производства отсутствуют, т.е. рассматривается некоторая ε – окрестность. Построим линию развития некоторого экономического показателя 
для экономического объекта за время ∆t до поверхности S2. Получим некоторый замкнутый объем w, обладающий поверхностью Г, который будем называть коридором развития показателя (рис.1).
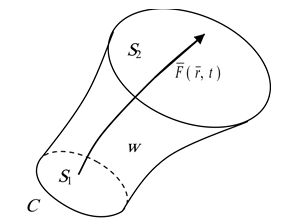
Рис. 1. Коридор развития показателя .
Параметрами, определяющими экономику, будут и экономическое состояние среды, описываемое коэффициентом сопротивления экономической среды η [1].
Рассмотрим частные случаи утверждений доказанных в работе [1], которые совпадают с утверждениями из работы [2].
Утверждение 1. Рассмотрим векторный экономический показатель 
, зависящий от факторов производства . Предположим непрерывность и существование первых непрерывных производных показателя внутри и на границах коридора развития. Тогда имеет место формула:
Проследим развитие векторного экономического показателя внутри некоторого объема w факторов производства с границей Г. Из утверждения следует, что поток векторного показателя на границе Г равен объемному интегралу от расхождения этого показателя.
Утверждение 2. Для скалярной функции 
, описывающей поведение некоторого скалярного экономического показателя, выделим в области развития ограниченный изменяющийся во времени объем факторов производства w. Предположим, что функция дифференцируема в выделенном объеме и на его границах. Будем считать, что объем w возникает из объема w0 = w(t0), где t0 — начальный момент времени, путем непрерывных изменений элементов w0 вдоль линий, определяемых вектором скорости обновления производственных факторов 
. Исходя из этого, имеет место равенство:
(1)
где 
.
Изучаемый объем факторов производства w под действием сил сопротивления экономической среды постоянно меняется. Из утверждения 2 следует, что для любого фактора производства p имеет место интегральное равенство:
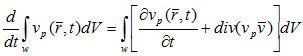
где p является одним из факторов производства 
.
Скорость обновления производственных факторов зависит от темпов освоения инвестиций для каждого момента времени, т.е. скорость зависит от изменяющегося объема факторов и сопротивления экономической среды, которая проявляется, в первую очередь, на факторах «расположенных» на границе изменяющегося объема. Изменение должно быть пропорционально объему этих факторов:
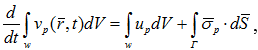(2)
где 
– противодействия развитию факторов производства со стороны экономической среды, , 
— освоенные инвестиции.
В правой части первое слагаемое описывает влияние инвестиций в целом на всю экономику системы, второе – противодействие экономической среды, которое уменьшает влияние инвестиций.
Изменение развития происходит для всех факторов, поэтому противодействие необходимо описывать в виде тензора σpl, где p,l — некоторые факторы производства:
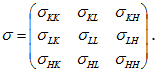
Тензор σpl назовем тензором сопротивления экономической среды. Для этого тензора на основании утверждения 1 имеет место равенство:
С учетом последнего уравнения равенство (2) примет вид:
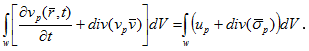
Объем факторов производства был выбран произвольным образом, поэтому имеем:
(3)
Тензор сопротивления должен зависеть от скорости изменения производственных факторов и некоторого коэффициента. Рассматриваемые факторы производства равноправные, поэтому тензор должен быть симметричный. Если градиенты скорости обновления производственных факторов не очень велики, то можем для описания тензора взять только скорости и первые производные от них. Это предположение является естественным ограничением для всех экономических объектов, нельзя достичь большой скорости развития при малом изменении факторов производства. Составим тензор из линейной комбинации произведения скоростей изменения 
и произведения скорости на производную скорости по факторам производства 
, 
. Производные высших порядков не включаем в σpl, так как всегда можно разложить любую функцию в ряд Тейлора и отбросить малые величины. Это самое главное ограничение на пути получения уравнения развития экономики с учетом влияния сопротивления среды.
Такой линейной комбинацией, удовлетворяющей перечисленным требованиям, может быть выражение:
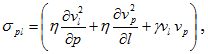(4)
где γ– безразмерный коэффициент пропорциональности. Коэффициент η отражает связь развития производственных факторов с инвестициями [3]. Большие значения η определяют не стабильность, а значение близкие к нулю указывают на эффективную экономику.
Подставим выражение (4) в уравнение (3), тогда для параметра имеем:
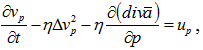(5)
где 
— оператор Лапласа, 
— освоенные инвестиции.
Полученную систему (5) назовем системой уравнений развития экономики с тензором сопротивления экономической среды. Это векторное уравнение является разновидностью уравнения Навье–Стокса.
Проблема существования решения уравнения Навье–Стокса вошла в список наиболее тяжелых математических проблем XXI столетия [4].
При изучении развития экономического объекта нетрудно получить интересный факт опираясь на простые соображения, которые связанны с размерностью экономических величин. Основа метода подобия и размерности базируется на том, что можно измерять все величины в единицах, которые являются характерными параметрами данной задачи.
Основные параметры физический капитал,трудовые ресурсыи человеческий капитал будем измерять в денежных единицах. При разном сочетании производственных факторов мы можем получить один и тот же объем производства, поэтому размер факторов производства будем оценивать через некоторый усредненный фактор 
.
Будем оценивать изучаемые факторы производства национальной экономики в единицах усредненного фактора производства ψ, скорость изменения факторов 
— в единицах vм (модуль скорости обновления производственных факторов мировой экономики или любой национальной экономики), так мы вводим безразмерные величины 
и 
. Время измеряем в единицах 
, а скорость освоения инвестиций — в единицах 
.
Равенство (5) для безразмерных величин примет вид:
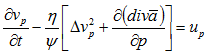(6)
В равенстве (6) все операторы и переменные являются безразмерными величинами. Получили, что каждый экономический объект обладает двумя параметрами: ψ и η. Эти величины имеют размерности:
[ψ] = ден. ед.; [η] = ден. ед.
Экономическим числом назовем величину:
Большие значения Е0 появляются при неустойчивом экономическом состоянии. Малые величины экономического числа указывают на «идеальное» состояние. Уравнение (6) при Е0 = 0 превращается в уравнение валовых инвестиций, которое применяется, например, в неоклассической модели роста.
Экономическое число обладает свойством, чем больше объем факторов производства или чем меньше экономическое сопротивление среды η, тем меньше Е0. Поэтому следует ожидать, что более развитые экономики должны обладать малыми значениями экономического числа.
Национальные экономики, получающиеся друг из друга в результате простого изменения масштаба производственных факторов и их скоростей, назовем подобными. Из определения следует, что национальные экономики, обладающие одинаковым экономическим числом являются подобными. Это свойство назовем правилом подобия национальных экономик.
Е. Букингем, опираясь на теорию анализа размерностей, предложил алгоритм нахождения безразмерных комплексов, который может быть применен к любому конкретному процессу [5]. Это правило было названо 
– теоремой. Определение размерности конкретных величин происходит через анализ размерностей величин, которые полностью характеризуют данный процесс. Опираясь на принцип однородности размерности полученных равенств, определяется характер зависимости выделенных величин. Именно этот принцип нашел свое отражение в – теореме.
Для использования этого алгоритма достаточно знать размерности основных переменных величин, которые характеризуют данный процесс. Важной особенностью и достоинством метода является отсутствия требования вида уравнения, описывающего изучаемый процесс.
Все слагаемые уравнений, определяющих экономический процесс, обладают свойством однородности по размерности. В нашем случае основными экономическими величинами могут быть время [T] и денежная единица [R]. Можно использовать другие независимые величины, которые позволяют описать процесс, например, экономическое сопротивление среды η и скорость изменения производственных факторов некоторого экономического объекта или модуль скорости .
Из – теоремы следует, что если nпеременных х1, х2, х3, … хn, которые участвуют в изучаемом процессе определить через выделенные переменные, то эти переменные группируются в п-m – членов, которые являются безразмерными:
, (7)
где pi являются безразмерным произведением нескольких xj. Каждый – член состоит из m+1 переменных величин. Для нашей задачи таких величин, которые входят в – члены, будет три. Экономическое сопротивление среды η и модуль скорости изменения производственных факторов 
будут определяющими величинами. Третья величина определяется изучаемой переменной.
Для простоты исследования третью величину возьмем в степени -1. Остальные показатели степени двух определяющих величин являются неизвестными.
Используя основные независимые переменные, находим остальные – члены, которые являются безразмерными для всех получаемых равенств. Показатель степени каждого из основных переменных должен быть нулевым.
Валовой объем продукции Y определяется основными факторами производства (в нашем случае мы используем усредненный фактор ψ), модулем скорости обновления производственных факторов v, объемом инвестиций I и сопротивлением экономической среды η.
На основании – теоремы должны получить систему уравнений, состоящую из трех – членов:
Определим размерности переменных полученной системы:
Опираясь на условие однородности, получим систему уравнений размерности для изучаемых – членов. Решением полученной системы будет:
Из полученных решений заключаем, что 
совпадает с экономическим числом. Член 
определяет критерий связи скорости изменения производственных факторов, от освоенного объема инвестиций. 
— член является критерием связи скорости изменения производственных факторов, от произведенного валового продукта.
Подставим – члены в (7) и найдем объем валового продукта Y:
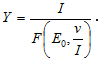
Из полученного равенства следует, что валовой продукт национальной экономики определяется экономическим числом, модулем скорости обновления производственных факторов и объемом освоенных инвестиций, которые вкладывается в развитие этих факторов.
В предельном случае, когда экономика приближается к «идеальной», т.е. 
, то полученные – члены примут вид: 
— экономическое число, 
— средняя склонность к инвестированию.
В результате преобразований получим линейную зависимость объема валового продукта, от объема освоенных инвестиций с некоторым безразмерным коэффициентом. Этот коэффициент зависит от экономического числа 
. Важным выводом из последнего равенства является зависимость склонности к инвестированию от экономического числа, и склонность к инвестированию равна 
.
Из – анализа можно сделать заключение, что кроме скорости обновления производственных факторов валовой продукт зависит от экономического числа.
Сделаем модельные расчеты для статистического анализа экономических чисел национальных экономик России и США. Статистические данные по человеческому капиталу отсутствуют, поэтому будем изучать некоторое приближение экономического числа, которое получим по двум факторам L — трудовые ресурсы, K — физический капитал.
Для объективности анализ все исходные данные для расчетов представим в долларах США, и приведем к ценам 2006 г. [6, 7, 8]. На рисунке ось абсцисс представляет собой временную ось, ось ординат показывает изменение значений 
(рис. 2).
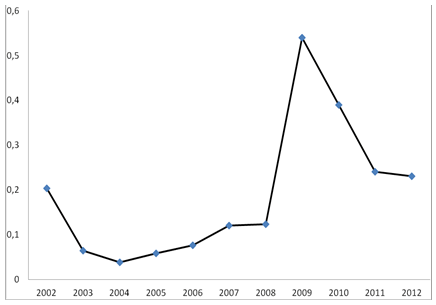
Рис. 2. Изменение российского экономического числа
Российское экономическое число Е0 имеет порядок 0,06–0,56 ед. Так, в 2007 г. оно равнялось 0,42, а в 2009 г. — 0,56. Из рисунка видно, что увеличение экономического числа началось в 2005 г. задолго до начала кризиса. Резкий скачок в числе произошел 2009 г. В последующие годы наблюдалось падение значений экономического числа.
Статистические данные для экономики США брались в ценах 1990 г. [6, 9] Экономическое число колеблется в пределах от -0,04 до 0,38. Отрицательные значения связаны с численной погрешностью вычислений. В США небольшое увеличение экономического числа началось в 2007 г. и в 2008 г. произошел большой скачок, далее происходило резкое падение и некоторая стабилизация (рис. 3).
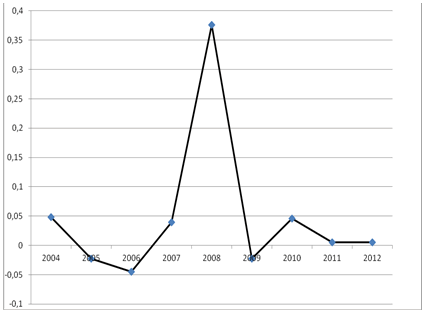
Рис. 3. Изменение экономического числа США
Мероприятия, проведенные в экономике США 2009 г., дали уменьшение числа, но в 2010 г снова произошел небольшой рост. В США экономическое число во все наблюдаемые годы было меньше самого минимального числа России, кроме кризисного года.
Анализ результатов показывает, что минимумы экономического числа соответствуют наибольшему подъему в экономике страны, а максимумы — указывают на появление кризисных явлений.
Модельные расчеты показали устойчивость показателя, его не случайность и объективность полученных результатов. Численные результаты указывают на возможность применения экономического числа как дополнительного инструмента при получении комплексных оценок таких сложных категорий как конкурентоспособность экономики и уровень экономического развития. Остается открытым вопрос о корректном измерении сопротивления экономической среды.
Читайте также
Библиографический список
- Кузнецов С.Б. Векторный анализ факторов производства. LAP LAMBERT Academic Publishing GmbH&Co, 2011.
- Кочин Н.Е. Векторное исчисление и начала тензорного исчисления. т.1. М.: Наука, 1965.
- Кузнецов С.Б. Моделирование экономических показателей. // Вестник ЧГУ. 2011. — №16(231), вып. 32. — с. 41-43.
- Smile S. Mathematical problems for next century. Mathematical Intelligencer. 1998. V.20, р. 7-15.
- Бриджмен П. Анализ размерностей. Ижевск: РХД, 2001.
- Conference Board CEO Challenge. URL: http//www.conference-board.org. (Дата обращения: 17.11.2014).
- Евростат [электронный ресурс]. URL: http://epp.eurostat.ec.europa.eu. (Дата обращения: 12.09.2014).
- Регионы России. Социально-экономические индикаторы [электронный ресурс]. – URL: http://www.gks.ru/wps. (Дата обращения: 11.11.2014).
- США. Бюро экономического анализа [электронный ресурс]. URL: http://www.bea.gov. (Дата обращения: 02.10.2014).
References
- Kuznecov S.B. Vector analysis of the factors of production [Vektornyj analiz faktorov proizvodstva]. LAP LAMBERT Academic Publishing GmbH & Co. 2011.
- Kochin N.E. Vector calculus and beginning of tensor calculus [Vektornoe ischislenie i nachala tenzornogo ischislenija]. V.1. M . Science .1965.
- Kuznecov S.B. Modeling of economic indicators [Modelirovanie jekonomicheskih pokazatelej]. Bulletin of the CSU . №16 (231), vol. 32, 2011. pp. 41-43.
- Smile S. Mathematical problems for next century. Mathematical Intelligencer. 1998. V.20. рp. 7-15.
- Bridzhmen P. Dimensional Analysis [Analiz razmernostej]. Izhevsk. RHD, 2001.
- Conference Board CEO Challenge. URL: http//www.conference-board.org/ (Date of access: 17.11.2014).
- Eurostat [Evrostat]. URL: http://epp.eurostat.ec.europa.eu. (Date of access: 12.09.2014).
- Regions of Russia. Socio-economic indicators [Regiony Rossii. Social’no-jekonomicheskie indikatory]. URL: http://www.gks.ru/wps/ (Date of access: 11.11.2014).
- U.S. Bureau of Economic Analysis (BEA) [SShA. Bjuro jekonomicheskogo analiza]. URL: http://www.bea.gov. ( Date of access: 02.10.2014).
