Использование нечеткой логики в оценке результатов тестирования персонала
The use of fuzzy logic in evaluating the results of testing personnel
Авторы
Аннотация
Целью статьи является разработка методики оценки результатов использования комплекса разнообразных тестов для получения интегральной оценки компетентности претендентов. В основу методики положены методы нечеткой логики и правдоподобных рассуждений. Данные методы позволяют унифицировать процесс тестирования при реализации методики в рамках экспертной системы адаптивного тестирования.
Ключевые слова
интегральный показатель отбора персонала, классификация претендентов, классификационные признаки, операции свертки критериев, уровни компетенций, нечеткий квантификатор.
Рекомендуемая ссылка
Астанин Сергей Васильевич,Жуковская Наталья Константиновна. Использование нечеткой логики в оценке результатов тестирования персонала // Современные технологии управления. ISSN 2226-9339. — №6 (54). Номер статьи: 5401. Дата публикации: 08.06.2015. Режим доступа: https://sovman.ru/article/5401/
Authors
Abstract
Purpose of the article is to develop a methodology for assessing the results of the use of the complex variety of tests to obtain an integrated assessment of the competence of applicants. The basis of the technique is the method of fuzzy logic and plausible reasoning. These methods make it possible to standardize the testing process for the implementation of the methodology in the framework of an expert system adaptive testing.
Keywords
the integral indicator of personnel selection, classification contenders, classification attributes, operations of convolution of criteria, levels of competence, fuzzy quantifier.
Suggested citation
Astanin Sergej Vasil'evich,Zhukovskaja Natal'ja Konstantinovna. The use of fuzzy logic in evaluating the results of testing personnel // Modern Management Technology. ISSN 2226-9339. — №6 (54). Art. # 5401. Date issued: 08.06.2015. Available at: https://sovman.ru/article/5401/
Введение
В практике отбора персонала многие предприятия используют тесты для выявления качеств претендентов. Сегодня используются разнообразные тестовые методики: тесты на профессиональную пригодность, общие тесты способностей, личностные тесты и т.д. Как правило, при отборе кандидатов используют не одну методику, а комплекс различных методик, направленных на всестороннюю оценку кандидатов. Такой подход связан с тем, что ни одна из перечисленных методик по отдельности не дает исчерпывающей информации, на основании которой можно было бы принять верное решение о приеме на работу. Однако проблема состоит в определении интегрального показателя оценки кандидатов на основании результатов тестирования по различным методикам. Практика тестирования персонала при приеме на работу показала, что в качестве метода отбора тесты могут быть использованы только в случае их подготовки высококлассными специалистами (профессиональные тесты), и практикующими психологами (психологические тесты). Тем не менее, зачастую, формированием интегрального показателя, занимаются некомпетентные сотрудники, оценка кандидатов которых, страдает субъективностью и неумением интерпретации результатов тестов. Выход из такой ситуации видится в разработке технологий и методик формирования интегральных показателей отбора персонала, ориентированных, с одной стороны, на профессиональные знания высококлассных менеджеров, с другой стороны, на особенности функционирования конкретного предприятия. Если учитывать тот факт, что человек, проводящий измерение знаний путем опроса или тестирования, сам влияет на его исход своим присутствием, своей предвзятостью, самой техникой тестирования или ее содержательной частью, то можно утверждать, что оценка получаемой информации носит в большей степени вероятностный характер. Существующие методы тестирования базируются на статистических данных, они достаточно объективны, но, тем не менее, не учитывают механизмы рассуждений менеджеров по персоналу, которые они используют при оценке претендентов. В этой связи актуальны методы оценки, основанные на методологии нечеткой логики. На наш взгляд такой подход целесообразен в связи с неопределенностью выявления уровней компетентности, связанных с человеческим фактором, как со стороны менеджера, так и со стороны претендента.
Классификация претендентов по уровням компетенций
Выбор метода классификации претендентов по уровням компетенций зачастую определяется исходя из общих свойств объектов классификации. Как известно, классификация — это система распределения объектов (предметов, явлений, процессов, понятий) по классам в соответствии с определенным признаком. Классификация позволяет сгруппировать объекты и выделить определенные классы, которые будут характеризоваться рядом общих свойств. В нашем случае классификация объектов — это процедура группировки на качественном уровне претендентов, направленная на выделение однородных уровней их компетенций. При классификации широко используются понятия классификационный признак и значение классификационного признака, которые позволяют установить сходство или различие объектов. При оценке компетенций в качестве классификационных признаков выделяют тип тестового задания (теста), степень соответствия ответа эталону и число правильно выполненных (соответствующих требованиям конкретной компетентности) тестовых заданий по каждому типу. Как было сказано выше, при классификации необходима интегральная оценка, учитывающая все классификационные признаки. В этой связи классификация предполагает решение следующих задач: выделение типов тестовых заданий, выбор метода классификации, построение интегральной оценки уровня компетенции. Признаки объектов классификации подразделяются на детерминированные, недетерминированные, логические и структурные [1]. Тип тестового задания и число правильно выполненных заданий по каждому типу относятся к детерминированным признакам, значения которых могут быть определены количественно и однозначно. Степень соответствия ответа эталону является качественным и неопределенным признаком, причем неопределенность имеет не случайный характер, и определятся субъективной мерой, используемой экспертом при оценке неточности ответа. Таким образом, при решении задачи классификации мы имеем совокупность детерминированных и недетерминированных признаков. Если для детерминированных признаков алгоритмы интегральной оценки известны и хорошо разработаны, то для недетерминированных признаков, характеризуемых неточностью и неоднозначностью, ситуация не столь очевидна.
Пусть заданы три множества Z1, Z2, Z3, определяющие число тестовых заданий по каждому типу соответственно. Одной из часто используемых операций свертки является операция осреднения вида [2]:
Q(Zi)=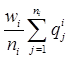
, (1)
где i
{1, 2, 3}, Q(Zi) — оценка знаний по группе тестовых заданий i-го типа, wi — вес тестового задания i-го типа, ni — число тестовых заданий i-го типа, qji — степень правильности ответа на j-е тестовое задание i-го типа.
Если qji
[0,1], то Q(Zi)
[0, wi]. Тогда, на шкале [0, wi] необходимо ввести оценки, например, интервальные, определяющие ту или иную степень знаний обучаемого по группе тестовых заданий i-го типа.
Очевидно, что такие оценки носят субъективный характер и определяются экспертным путем. Однако, эксперты, на наш взгляд, не используют подобный механизм оценки знаний, и, кроме того, в формуле (1) не учитывается один из введенных признаков классификации — число правильных ответов.
Следует также отметить, что применение формулы (1), не дает интегральной оценки знаний по всем типам тестовых заданий и, следовательно, необходимо обоснование некоторого оператора, позволяющего получение интегральной оценки на основе частных оценок по каждому типу тестовых заданий.
Использование процедур классификации в пространстве введенных признаков, также является трудноразрешимой задачей, как по причине присутствия качественного признака, так и по причине необходимости экспертной идентификации классов, сформированных в процессе разбиения обучающей выборки. Кроме того, в этом случае необходимо статистическое обоснование выборки, например, по критерию c2.
Исходя из сказанного, необходимо разработать такой механизм классификации, который бы позволял однозначное толкование классов, был бы независим от числа элементов обучающей выборки и не имел недостатков присущих операциям свертки критериев вида (1).
В связи с тем, что в идентификации классов, разрешении проблемы неопределенности при интерпретации значений признаков и обосновании операторов свертки, значительная роль отводится экспертам, для решения задачи классификации обучаемых будем использовать методологию нечеткой логики.
В соответствии с [3] неопределенность и неточность рассматриваются как две противоположные точки зрения на одну и ту же реальность — неполноту информации, причем информацию можно выразить в форме логического высказывания, содержащего предикаты и квантификаторы. Предикаты интерпретируются как подмножества одного и того же универсального множества. Высказывание может также рассматриваться как утверждение, относящееся к появлению некоторого события. Неточность относится к содержанию информации, а неопределенность к ее истинности, которая понимается в смысле соответствия действительности. Основываясь на схеме разветвленного программирования [4] будем использовать три варианта ответов на каждый тип тестовых заданий: правильный ответ, неточный ответ и неправильный ответ. Так как приводимые ниже рассуждения характерны для любого типа тестовых заданий, возьмем для рассмотрения любой из них, например, третий тип. В качестве операторов свертки, позволяющих оценивать результаты решения каждой группы тестовых заданий, используем сложные высказывания:
1) если большинство задач данного класса сложности решены правильно, то оценка «отлично» для данного класса сложности (правила базы знаний). Формально: Q1Ai
Bi, i
{1, 2, 3}, где Ai и Bi — предикаты, определяющие правильность и оценку решения тестовых заданий i-го типа сложности; Q1 — квантификатор «большинство»;
2) если большинство задач данного класса сложности решены неточно или многие задачи данного класса точности решены правильно, то оценка «хорошо для данного класса сложности» (правило базы знаний). Формально: Q2Ci
Q4Ai
Di, i
{1, 2, 3}, где Ci, Ai и Di — предикаты, определяющие неточность, правильность и оценку решения тестовых заданий i — го типа; Q2 и Q4- квантификаторы «большинство» и «многие» соответственно;
3) если некоторые задачи данного класса сложности решены правильно или некоторые задачи данного класса сложности решены неточно, то оценка «удовлетворительно» для данного класса сложности» (правило базы знаний). Формально Q3Аi
Q5Сi
Fi, где Ai, Ci и Fi — предикаты, определяющие правильность, неточность и оценку решения тестовых заданий i-го типа; Q3 и Q5 — квантификаторы «некоторые»;
4) если нет задач, решенных правильно или с неточностью, то оценка «неудовлетворительно» или формально 
(Ai
Ci)
Ji, Ai, Ci и Ji — предикаты, определяющие правильность, неточность и оценку решения тестовых заданий i-го типа.
Используемые квантификаторы могут быть описаны, в терминах нечетких множеств, следующим образом: Qr={(z, 
(z))}, r=
{1, 2, 3, 4, 5}, где z — элементы универсального множества Zi, 
:Zi
[0,1].
На рис.1 показан пример задания квантификаторов для 10 тестовых заданий третьего типа.
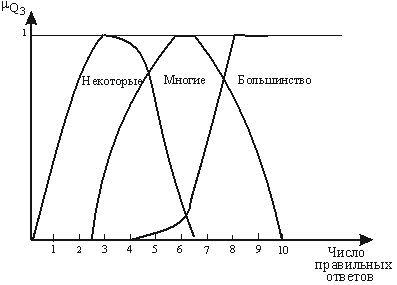
Рис.1. Задание нечетких квантификаторов по числу правильных ответов
Такое представление квантификаторов является простой процедурой для экспертов, а приведенных выше правил 1) — 4) достаточно для выявления уровня компетенций по i-й группе тестовых заданий. Аналогичным образом следует поступать при определении операторов свертки для первого и второго типа тестовых заданий. В результате мы имеем 12 утверждений, причем их структура соответствует структуре продукционных правил базы знаний экспертной системы.
Следовательно, при организации процедуры классификации можно воспользоваться алгоритмами обработки, используемые в системах искусственного интеллекта.
В [5] приводятся схемы рассуждений с нечеткими квантификаторами. В частности, рассмотрены утверждения с нечеткими квантификаторами, моделируемыми нечеткими подинтервалами интервала [0,1]:
Q1A есть B
Q2(A&B) есть C
(Q1
Q2)A есть (B&C).
Такую схему рассуждений, с точки зрения причинно-следственных отношений, можно интерпретировать следующим образом:
1. Если наблюдается событие A, то произойдет событие B;
2. Если одновременно наблюдаются события A и B, то произойдет событие C;
3. Из утверждений 1 и 2 следует, что если наблюдается событие A, то произойдут события B и C.
Здесь роль квантификаторов сводится к ограничению истинности рассматриваемых утверждений на основе функций, причем 
, вычисляется на основе 
и 
. Такая схема позволяет выводить новые заключения по утверждениям 1, 2 и при наблюдении события A.
Аналогичным образом для оценки уровня компетенций для любого типа тестовых заданий возможно получение новых заключений при наблюдении фактов, не вошедших в утверждения 1) — 4).
Основной проблемой при этом будет проблема определения операции «*». С учетом заданных квантификаторов Q1 — Q5 (рис.1), система классификации автоматически может формировать следующие схемы рассуждений, соответствующие i-му типу тестовых заданий и утверждениям 1) — 4):
I.
Q1Ai
Bi
Q1Ai
Q3Ci
(Q1*Q3)(Ai&Ci)
Bi
Схема позволяет на основе утверждения 1) и фактов Q1Ai, Q3Ci оценить достоверность заключения Biза счет вычисления функции.
II.
Q2Ci
Q4Ai
Di, Q2Ci
Q4Ai
Di
Q2Ci Q4Ai
Q3Ai Q5Ci
(Q2*Q3)(Ci&Ai)
Di (Q4*Q5)(Ai&Ci)
Di
III.
Q3Ai
Q5Ci
Fi
Q3Ai
Q5Ci
(Q3*Q5)(Ai&Ci)
Fi
Если высказывания 1) — 4) определяют заключения с достоверностью, ограниченной соответствующими квантификаторами, то схемы рассуждений I, II, III определяют заключения с достоверностью, ограниченной комбинацией квантификаторов.
Следует отметить, что при применении схемы рассуждений 4), оценка достоверности заключения J вычисляется следующим образом: 
=1-
=1-
.
Лингвистическая шкала оценки
В [6] рассмотрен подход к использованию алгоритмов комбинирования свидетельств, в случае неполной информации об объекте. Суть подхода состоит в применении функций, позволяющих оценивать достоверность заключения о состоянии объекта на основе частных утверждений, содержащих описания отдельных признаков. Так, если G1, G2, … , Gn — множество утверждений вида s1
r, s2
r,…, sn
r, где s1, s2,…, sn — множество значений признаков, описывающих некоторый объект; r — заключение о состоянии объекта, то достоверность заключения вычисляется следующим образом [7]:
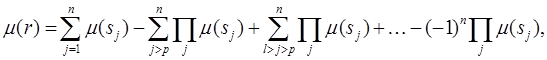(2)
где µ(sj), j=1, 2, …, n — достоверности признаков sj частных утверждений Gj; µ(r) — оценка достоверности заключения, сформированная на основе частных утверждений. Формула (2) представляет собой общий случай операции объединения нечетких множеств, заданных на разных предметных шкалах. В том случае, если признаки задаются на одной предметной шкале, в качестве операции объединения используется операции «max». Для оценки достоверности заключений схем рассуждений A, B, C формула (2) примет следующий вид: µr=
=q1+qk—q1qr, где q1 и qk — значения соответствующих квантификаторов, полученные в зависимости от конкретного числа правильных и неточных ответов.
Таким образом, в результате применения высказываний 1-4 и схем рассуждений I, II, III получаем достоверности оценок для каждого типа тестовых заданий: µBi, µDi, µFi, µJi, где верхний индекс (i=1, 2, 3) определяет тип тестового задания. Другими словами, претендент оценивается по отношению к каждому типу сложности тестовых заданий.
Оценки «отлично» (B), «хорошо» (D), «удовлетворительно» (F) будем интерпретировать как частные критерии уровня компетенций претендента. Для получения итоговой оценки можно было бы воспользоваться, описанным выше, подходом на основе экспертных утверждений. Однако, так как частные критерии неравнозначны, что определяется значениями частных оценок µBi, µDi, µFi, µJi, экспертные заключения могут носить субъективный и, зачастую, несовпадающий характер. В этой связи использовать этот подход для получения итоговой оценки нецелесообразно.
Пусть Ω — множество претендентов, которые требуется классифицировать с учетом данных критериев. Будем выделять три класса объектов в соответствии с тремя категориями оценки компетенций: «отлично», «хорошо», «удовлетворительно». С каждым классом будем связывать обобщенные целевые функции Gl (l=1, 2, 3), каждая из которых выражается посредством частных целей, связанных с критериями B, D, F, соответственно. Тогда множество претендентов, совместимых с какой-либо целевой функцией, можно получить путем свертывания частных целей, определяемых нечеткими оценками µBi, µDi, µFi.
В [3] обосновано применение идемпотентной симметрической суммы в качестве операции свертки для случая неравнозначных критериев. Симметрическая сумма для m критериев определяется следующим образом:
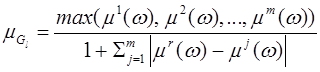, j
r, (3)
где µr(ώ) — наиболее значимый критерий.
Для нашего случая особенность использования формулы (3) заключается в следующем. В том случае, когда какая-нибудь из оценок µBi, µDi, µFiявляется допустимой, т.е. имеет значение равное или большее порогового, то наиболее значимым критерием является B (высокая компетентность, ориентированная на тестовые задания третьего типа). При этом критерии D и F являются дополнительными при оценке уровня знаний. В этом случае формула (3) примет следующий вид:
.
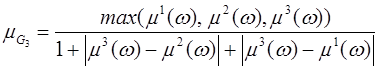Если ни одна из оценок µB3, µD3, µF3 не является допустимой, но среди оценок µB2, µD2, µF2 имеется допустимая оценка, то значимым критерием становится D, а дополнительным — критерий F. В этом случае критерий B во внимание не принимается. Формула для вычисления целевой функции будет следующей:
.
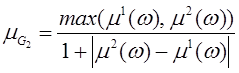И, наконец, если среди оценок µB1, µD1, µF1 имеется допустимая оценка, причем ни одна из оценок µB2, µD2, µF2, µB3, µD3, µF3 не является допустимой, то значимым будет являться критерий G1. В этом случае формула (3) примет вид: 
=
. Следует отметить, что в оценках µBi, µDi, µFi не учитывается неравнозначность критериев B, D, F. Распространенным методом выражения различий критериев по важности является назначение каждому из них некоторого веса с последующим суммированием этих весов в рамках операции свертки. Как правило, априорная оценка весов критериев весьма проблематична. Однако, в случае вычисления целевых функций оценки знаний, естественно воспользоваться рейтинговой системой, в рамках которой закреплены распределения баллов относительно категорий оценки компетенций: «отлично», «хорошо», «удовлетворительно».
Данным категориям соответствуют следующие интервалы процентной шкалы: «отлично» — [85-100]; «хорошо — «[70-84], «удовлетворительно» — [55-69]. Переходя от процентной шкалы к нормированной шкале [0, 1] получим интервалы [0.85-1], [0.7-0.84], [0.55-0.69]. Обозначим подинтервалы нормированной рейтинговой шкалы через Аk (k=1, 2, 3), а шкалу оценок по частным целям через М. Отобразим оценки по частным целям µBi, µDi, µFiв соответствующий Аk по следующей формуле:
,
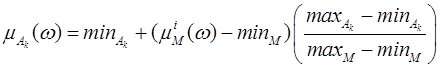где min
, min
, max
, max
— минимальные и максимальные значения шкал Ak и M соответственно. Если подставить в формулу (3) 
вместо 
, то можно получить значения целевых функций с учетом неравнозначности критериев, т.е.
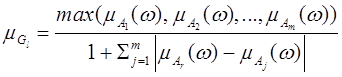
После вычисления значений целевых функций по формуле (3) встает вопрос об их интерпретации по отношению к рассматриваемым классам. Очевидно, что для целевых функций с значениями 
=1 нет проблем с интерпретацией. Так, например, для G3 c 
=1 характерно следующее правило классификации: если претендент по всем типам тестовых заданий получил отличные оценки, то с абсолютной уверенностью он относится к классу «отлично». Для других комбинаций оценок по разным типам тестовых заданий ситуация не столь очевидна. Приведенному правилу классификации можно поставить в соответствие формальное правило вида Sp: если A1 и А2 и … и Am то Gl, 
. Для нашего случая A1, А2, …, Am представляют собой значения признаков объекта классификации, Gl — класс объектов классификации, а 
[0,1] — оценка неопределенности правила Sp. Оценка неопределенности правила рассматривается как функция Gl: [0,1]®L, где L — множество лингвистических значений, определяющих уверенность в заключении Gl. Например, L={«невозможно», «сомнительно», «возможно», «абсолютно»} может определять степени уверенности в принадлежности объекта к тому или иному классу (рис.2).
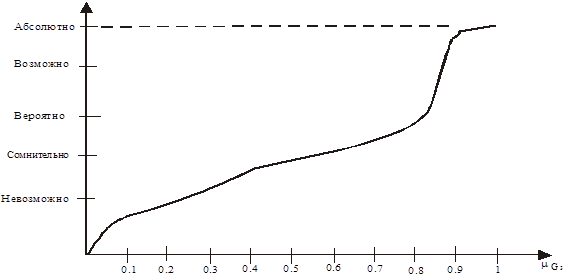
Рис.2. Пример отображения целевой функции в класс «отлично»
Модель, учитывающая градации принадлежности объекта к классам, представляется следующим образом. Для каждого класса задается функция вида Gl:
L и одно правило классификации с 
=1.
На основе вычисленных оценок целевых функций определяется лингвистическая принадлежность претендента к одному из классов. Преимущество модели состоит в отсутствии необходимости представления всего спектра возможных правил классификации, в связи с тем, что используется автоматическая генерация правил, основанная на свертке нечетких квантификаторов.
Заключение
Рассмотренный подход к оценке результатов тестирования персонала и классификации претендентов ориентирован на построение модели тестируемого и ее учете при оценке компетенций. Предложенная модель позволяет перейти к тестированию персонала с единых позиций. Применение процедурного подхода к обработке нечетких квантификаторов при формировании модели позволяет использовать неполную базу знаний с последующим ее расширением без потери адекватности решаемым задачам. В силу несложности используемого математического аппарата модель легко программируема, что позволяет использовать ее в экспертных системах адаптивного тестирования. Рассмотренный подход к интегральной оценке компетенций при отборе персонала ориентирован на использование комплекса разнообразных тестов. В дальнейшем, на основе подхода, предполагается разработка методики формирования команд исполнителей.
Читайте также
Библиографический список
- Вапник В.Н., Червоненкис А.Я. Теория распознавания образов.– М.: Наука, 1974.– 415с.
- Keeney R.L. and Raiffa H. Decisions with Multiple Objectives//Preferences and Value Tradeoffs. New York: Wiley, 1976.–569 pp.
- Дюбуа Д., Прад А. Теория возможностей. Приложения к представлению знаний в информатике.–М.: Радио и связь, 1990.–288с.
- Краудер Н.А. О различиях между линейным и разветвленным программированием /В сб. «Программированное обучение за рубежом».–М.: Высшая школа, 1968.– С.58-67.
- Астанин С.В. Правдоподобные рассуждения в системах принятия решений.–Таганрог: ТРТУ, 2000.– 90с.
- Астанин С.В., Грицанов А.А., Жуковская Н.К. Автоматизированная система оценки знаний на основе нечеткой логики//Телекоммуникации и информатизация образования, 2002. №4.– С.57-67.
- Сметс Ф. Простейшие семантические операторы /В кн.: Нечеткие множества и теория возможностей /Под ред. Р. Ягера. –М.: Радио и связь, 1986.–408с.
References
- Vapnik V.N., Chervonenkis A.Ja. The theory of pattern recognition [Teorija raspoznavanija obrazov]. Moscow. Nauka, 1974. 415p.
- Keeney R.L. and Raiffa H. Decisions with Multiple Objectives//Preferences and Value Tradeoffs. New York. Wiley, 1976. 569p.
- Djubua D., Prad A. The theory of possibilities. Applications to knowledge representation in computer science [Teorija vozmozhnostej. Prilozhenija k predstavleniju znanij v informatike]. Moscow. Radio and communication, 1990. 288p.
- Krauder N.A. On the difference between linear and intrinsic programing [O razlichijah mezhdu linejnym i razvetvlennym programmirovaniem]. In the collection. Programmed learning abroad. Moscow. Higher school, 1968. pp. 58-67.
- Astanin S.V. Plausible reasoning in the decision-making systems [Pravdopodobnye rassuzhdenija v sistemah prinjatija reshenij]. Taganrog. TRTU, 2000. 90p.
- Astanin S.V., Gricanov A.A., Zhukovskaja N.K. Automated Testing System based on fuzzy logic [Avtomatizirovannaja sistema ocenki znanij na osnove nechetkoj logiki]. Telecommunications and Information Education, 2002. №4. pp.57-67.
- Smets F. Simple semantic operators [Prostejshie semanticheskie operatory]. In the book. Fuzzy sets and possibility theory Ed. R. Yager. Moscow. Radio and Communications, 1986. 408p.
