Управление в условиях неопределенности
Management in conditions of uncertainty

Авторы
Аннотация
Статья описывает применение методов серого реляционного анализа для управления в условиях неопределенности. Раскрывается информационная ситуация для белого и серого анализа. Серый пространственный анализ в качестве основного объекта анализа использует информационную ситуацию. Количественные методы анализа используют интервальные, треугольные и трапециевидные числа в дополнении к точечным числам. Серый пространственный анализ близок к теории нечетких множеств и дополняет эту теорию. В отличие от теории нечетких множеств серый анализ допускает возможность перемены цели и множество критериев управления.
Ключевые слова
управление, неопределенность, управленческие задачи, многоцелевое управление, множественность решений, ситуационное моделирование, ситуационное управление, информационные ситуации, многокритериальность
Рекомендуемая ссылка
No items found. Управление в условиях неопределенности // Современные технологии управления. ISSN 2226-9339. — №7 (79). Номер статьи: 7902. Дата публикации: 31.07.2017. Режим доступа: https://sovman.ru/article/7902/
Authors
Abstract
The article describes the application of gray relational analysis methods for management under uncertainty. The article describes the information situation for white and gray analysis. Gray spatial analysis uses the information situation as the main object of analysis. Quantitative methods of analysis use interval, triangular and trapezoidal numbers in addition to point numbers. Gray spatial analysis is close to the theory of fuzzy sets and complements this theory. Gray analysis allows the possibility of changing the goal and a variety of management criteria. This distinguishes the gray analysis from the theory of fuzzy sets.
Keywords
Management, uncertainty, management tasks, multipurpose management, multiplicity of decisions, situational modeling, situational management, information situations, multicriterial
Suggested citation
No items found. Management in conditions of uncertainty // Modern Management Technology. ISSN 2226-9339. — №7 (79). Art. # 7902. Date issued: 31.07.2017. Available at: https://sovman.ru/article/7902/
Введение
Управление в условиях информационной неопределенности занимает важное место в общей проблеме управления [1]. Различают информационную и ситуационную неопределенность. Успешное решение задач управления невозможно без применения специальных подходов, информационных и интеллектуальных технологий. Затрудняет решение проблемы различные трактовки понятия «неопределенность». Задачи управления в условиях неопределенности обусловлены разными факторами. Например, управленческая информация может представлять представляют собой слабоструктурированные или неструктурированные информационные комплексы. Управленческая информация может содержать нужную информацию, но иметь большой объем или высокую сложность, что делает ее не обозримой или не воспринимаемой. Управленческая информация может содержать полезную и бесполезную информацию, а иногда даже дезинформацию. Для описания неопределенности теория принятия решений широко применяет аппарат теории нечетких множеств [2-4]. Однако этот подход является частным случаем и не охватывает все ситуации информационной неопределенности. Следует отметить общий недочет существующей теории учета неопределенности для задач управления. Реальное управление рассматривает не только объект управления, но окружающую его ситуацию. Но в теории управления не рассматривают информационную ситуацию ни как объект управления, ни как фактор управления. Это и создает информационную неопределенность в управлении. В настоящее время всё большее внимание уделяется разработке новых подходов к анализу сложных информационных ситуаций, но информационная ситуация не рассматривается как объективный феномен управления. Одним из методов управления является так называемый «серый» информационный анализ.
Использование серого анализа
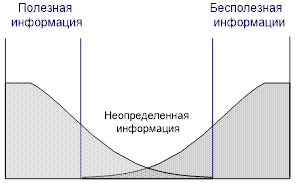
Во многих случаях постановка задачи управления предполагает принятие решений в условиях неполной информации. На практике управление в условиях неопределенности имеет место всегда. Различие составляет степень неопределенности. Простейшая модель управленческой информации представлена на рис.1. Всегда в распоряжении лица принимающего решение имеется в распоряжении информация, нужная для достижения цели и ненужная информация. В ненужную информацию всегда попадает дезинформация, которая представляет собой вредную информацию. Поэтому с позиций управления всегда существует необходимость альтернативы: выбор полезной информации по критерию достижения цели и выбор бесполезной для достижения цели информации.
Рис.1. Управленческая информация двух качеств
Для ситуаций, неопределенность информации которых составляет от 20% и больше, применяют термин «серый» анализ и «серые» системы. Отсюда управление в условиях неопределенности связывают с «серым анализом». Следует отметить, что «серый анализ» является одним из методов подготовки управленческих решений в условиях неопределенности.
Понятие «серые» системы существует с 90-х годов [5]. Термин «серый анализ» применяют в реляционном [6, 7] и корреляционном анализе [8-10]. Серый управленческий анализ использует информационный подход [11-14] и модель информационной ситуации [15-19].
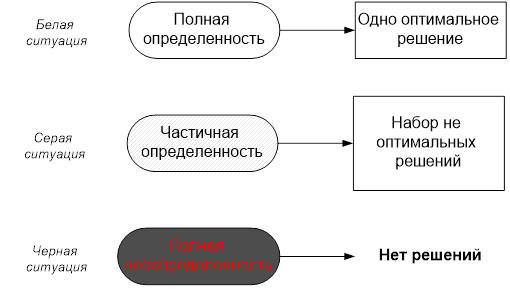
Серый анализ определяет информационную ситуацию без необходимой информации как «черную», а ситуацию с полной информацией как «белую» Рис.2. На рис 2 имеется под словом определенность имеется ввиду информационная определенность. Поскольку крайних ситуаций не бывает, то в реальных задачах всегда существует частичная определенность и частичная неопределенность [20].
Все реальные ситуации между этими двумя крайностями описываются как «серые» или размытые. Таким образом, «серая» система анализа означает, что исследуется ситуация, в которой часть информации известна и часть информации неизвестна.
Рис.2. Место «серого» анализа в принятии решений
При таком определении количество и качество информации образуют континуум, от полного отсутствия информации до полной информационной определенности (рис.2). От черной ситуации через серую ситуацию до белой ситуации.
Серый анализ заключается в поиске набора обобщенных решений. Для «черной» ситуации решений нет. Для «белой» ситуации существует одно оптимальное решение. «Серые» системы анализа будут давать различные возможные решения по информации в ситуации. Серый анализ не пытается найти лучшее решение. Он заключается в категоризации и группировке решений по признакам: «допустимое решение», «хорошее решение», «подходящее решение» и т.д. для реальных проблем. То есть по существу он решает задачи поддержки принятия решений, а не задачи принятия решений. С другой стороны он допускает последующий когнитивный [21, 22] или интеллектуальный анализ [23].
Пространственное моделирование в сером анализе
При решении задач управления часто применяют пространственное моделирование, если объектами управления являются пространственные объекты. Пространственное моделирование, как метод научного познания, прошло достаточный период развития. По мере роста сложности задач, решаемых методами пространственного анализа, развития пространственных моделей, совершенствования программного обеспечения, появления новых технологий сбора информации – совершенствовались и развивались методы пространственного моделирования.
В настоящее время возник новый вид моделирования – пространственное ситуационное моделирование [15, 24], которое тесно опирается на методы геоинформатики. Ситуационное моделирование возникло в 80-е годы в области искусственного интеллекта [25]. Однако аппарат этого моделирования не позволил применить этот подход непосредственно в менеджменте. Хотя его переводят на английский как “Situational Management”, по существу это Situational Control. Он был ориентирован на интеллектуальное и автоматизированное управление
Как реакция на западе возник ситуационный менеджмент [26, 27], который ориентирован в первую очередь на организационное управление. В этом свете пространственное ситуационное моделирование возникло как «серая» ситуация, которая находится между организационным ситуационным управлением и интеллектуальным управлением. Специфика пространственного ситуационного управления в использовании пространственной информации, пространственных отношений и методов геоинформатики.
Ситуационное моделирование и пространственное ситуационное моделирование [24] делится на две группы стационарное и динамическое. Стационарное моделирование описывает различные статические ситуации. Динамическое моделирование применяется для анализа динамики ситуаций.
Стационарное моделирование рассматривает в качестве объекта исследования стационарную информационную ситуацию и объект в этой ситуации или изменение позиции объекта в этой ситуации. Динамическое ситуационное моделирование рассматривает в качестве объекта исследований динамическую информационную ситуацию и не только объект в этой ситуации, но и комплекс разных объектов. Оно включает моделирование ряда компонент как зависимых сложных систем: объекта исследования; среды вокруг объекта; системы отношений и вытекающих из них связей «объект-среда». Поэтому для понимания специфики ситуационного моделирования необходимо рассмотреть пространственные отношения.
Пространственные отношения в сером анализе
Основой ситуационного пространственного стационарного о моделирования являются геоданные [28] и информационные отношения [29]. Многие виды стационарного пространственного моделирования используют пространственные отношения. При ситуационном моделировании пространственные отношения играют доминирующую роль как инструмент описания именно ситуаций, в которой находится объект моделирования или группа объектов. Пространственные отношения задают описание начальной ситуации и определяют динамику ее развития. Связи «объект – среда», которые были упомянуты выше, в геоинформатике задают именно пространственные отношения. Следует подчеркнуть, что пространственные отношения не эквивалентны связям, а только задают условия для их возникновения, существования и развития.
Особенность ситуационного моделирования в том, что во внимание принимается объект моделирования и окружающая его микро ситуация или микросреда. Совокупность развития ситуаций образует сценарий. Возможны 4 типа развития простых ситуаций (сценариев), они приведены в таблице 1.
Таблица 1 — Сценарии развития ситуаций
| Модель объекта стационарная | Модель объекта динамическая | |
| Среда стационарная | Сценарий 1 | Сценарий 2 |
| Среда динамическая | Сценарий 3 | Сценарий 4 |
Сценарий 1 соответствует стационарному моделированию. Остальные 2-4 приводят к динамическому моделированию. Динамику среды задают пространственные отношения. Они же определяют характер взаимодействия объекта и среды.
В более сложном случае ситуационное моделирование включает исследование выбранного объекта, который можно назвать основным и группу вспомогательных объектов. Например, при мониторинге деформаций и осадок в процессе строительства основного сооружения наблюдение ведется за этим основным объектом, Но при этом отслеживают окружающие объекты, которые также могут испытывать смещения и осадки, обусловленные строительными работами. Совокупность развития ситуаций в этом случае схематически приведена в таблице 2.
Таблица 2 — Сценарии развития ситуаций при учете совокупности объектов
| Среда стационарна | Среда динамическая | |
| Модель основного объекта стационарная | Сценарий 1 | Сценарий 2 |
| Модель основного объекта динамическая | Сценарий 3 | Сценарий 4 |
| Совокупность окружающих объектов стационарная | А | Б |
| Совокупность окружающих объектов динамическая | В | Г |
В этом случае ситуация А «и» сценарий 1 соответствует стационарному моделированию. Ситуации А – сценарии 2-4, Б сценарии 2, 4, В – сценарии 1-4, Г – сценарии 1-4 — требуют проведения пространственного динамического моделирования. Таким образом, в реальной практике при исследовании совокупности объектов чаще всего требуется проведение ситуационного пространственного моделирования. Основой такого моделирования являются пространственные отношения.
На практике пространственные отношения имеют четыре основных вида: иерархические, топологические, геореференцные и геостатистические. Первые два вида в явной форме задают отношения порядка. Вторые два вида представляют собой неявное знание [30] и требуют достаточно кропотливой обработки для получения явного знания. Иногда выделяют более мелкие пространственные отношения такие как «тангенциальные», «конфигурационные», «координатные». Иерархические пространственные отношения наиболее ярко проявляются в кадастре. В этой сфере имеет место четкая иерархия кадастровых объектов, которая используется при землепользовании, в государственном управлении при учете природных и земельных ресурсов. Она не допускает перекрытие объектов одного уровня иерархии.
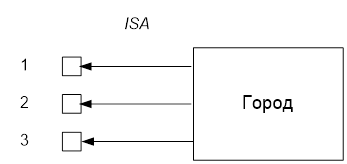
Самым распространенным типом пространственных отношений при изучении пространственных объектов является иерархический тип, описывающий отношения между элементами, множествами и частями объектов. Это отношения типа «один ко многим». Однако пространственные отношения включают еще отношения «многие ко многим». Наиболее распространенные пространственные отношения обозначают ISA, AKO Рис.3.
Рис.3. Пространственные отношения типа ISA
Условно: 1- инженерное сооружение; 2- переход; 3 –дорога.
Отношение классификации ISA происходит от английского “is a”. Говорят, что множество (класс) классифицирует свои экземпляры (например, “улица есть часть городской территории). Иногда это отношение именуют “member of”. По-русски это может называться «есть» (единственное число) или «суть» (множественное число). Связь ISA предполагает, что свойства объекта наследуются от множества. Эти отношения используют при описании городской ситуации.
Обратное отношение – “example of” или «пример». Поэтому процесс порождения элементов из множества называется экземпляцией.
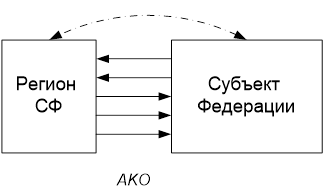
Отношение между множеством и подмножеством AKO (рис.4) происходит от английского “a kind of”, например, «городские районы есть подмножество городской территории».
Рис.4. Пространственные отношения типа AKO
Отличие AKO от отношения ISA заключается в том, что ISA – отношение «один ко многим», а AKO отношение – «многое к многим». С позиций геоинформатики отношение ISA применяют для описания ситуаций на картах в крупных масштабах. Отношение AKO применяют для описания ситуаций на картах в мелких масштабах.
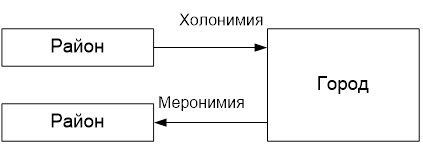
Применяя пространственные отношения, следует четко различать, какие объекты являются классами, а какие – экземплярами классов. При этом вовсе не обязательно одно и то же понятие будет классом или экземпляром во всех предметных областях. Например, «студент» всегда будет классом в базах знаний типа «студенческая группа» или «вуз», но может быть экземпляром класса учащихся. Наличие отношения классификации еще не говорить о существовании системы классификации, а только служит основой для нее. Исключение составляют те случаи, когда классификация уже создана. Объект, как сложная система, состоит из нескольких частей и элементов. Например, город включает улицы, площади, дома, объекты инфраструктуры, инженерные сооружения и т. д. Это определяет еще один тип отношения – Отношение целого и части. Их также называют отношениями меронимии и холонимии (рис.5).
Рис.5. Отношения холонимии и меронимии
Отношение меронимии – отношение целого к части (“has part”). Мероним – объект, включающий другой объекта как часть. «Город включает городские районы. Городская территория включает улицы». Отношение холонимии – отношение части к целому (“is a part”). «Улица часть городской территории». Улица – холоним для городской территории. Городская территория – мероним для улицы.
Говоря об иерархических пространственных отношениях, следует упомянуть об уровнях иерархии и отметить, что существуют семантические отношения на одном уровне иерархии и отношения между уровнями. Отношения на одном уровне соответствуют парадигматическим отношениям, отношения между уровнями соответствуют синтагматическим отношениям. Эти отношения задают семантику ситуационного моделирования в геоинформатике.
Топологические отношения широко используются в картографии и на транспорте. Для описания топологических отношений пространственных объектов широко применяют графовые модели. В этих моделях могут быть использованы разные виды отношений. При этом следует отличать пространственный граф, который содержит пространственную топологию от информационного графа, например семантической сети. При моделировании топологических отношений используют следующие виды отношений:
- функциональные (определяемые обычно глаголами «производит», «влияет»…);
- количественные (больше меньше, равно…);
- позиционные (далеко от, близко от, за, под, над…);
- временные (раньше, позже, в течение…);
- атрибутивные (иметь свойство, иметь значение);
- логические (И, ИЛИ, НЕ);
- лингвистические.
Геореференцные отношения представляют собой специфический лингвистически-информационный инструмент фиксации отношений пространственных номенов и понятий, а также географических названий. Геореференция в разных формах отражает отношения между пространственно локализованными объектами и информацией об этих объектах. Она часто нелинейна, многозначна и порой бывает неявной. Это означает, что она выражается в категориях неявного знания [30].
В сферу геореференции входят также зависимости между любой документальной информацией (например, карты, космические снимки, биографическая информация) и географической локализацией с помощью местонаименований, кодов места (например, почтовые коды), координат и других методов, описывающих пространственные связи и отношения. Существуют специальные справочники географических названий и так называемые газеттиры, которые отражают отношение геореференций. В ГИС геореференция отражается с помощью так называемых ассоциативных связей. Вне ГИС она отражается различными лингвистическими конструкциями.
Формализация ситуационного моделирования
Ситуационное моделирование в аспекте управления соотносится со «школой управления при непредвиденных обстоятельствах». Концепции этой школы, называемой в оригинале contingency school of management [31], строятся на том, для всех случаев жизни нет никакого единственного универсального способа управления. Каждая ситуация уникальна. Не существует единого для всех «лучшего» способа управления во всех ситуациях. Школа управления при непредвиденных обстоятельствах концентрирует внимание на том, что пригодность различных методов управления определяется конкретной ситуацией. Самым эффективным методом управления в конкретной ситуации является метод, который более всего соответствует данной ситуации. Задача — найти и суметь реализовать этот метод. Реализацией этого метода в пространственных ситуациях является пространственное ситуационное моделирование.
Ситуационное моделирование предполагает моделирование объектов, как связанных, так и меняющихся систем. При визуализации такого моделирования аналогом будет видеофильм или видеозапись. Структурно ситуационное моделирование опирается на ряд специализированных моделей. Основой ситуационного моделирования является предварительное создание языка моделирования, то есть создание различных информационных единиц. Это могут быть: графические информационные единицы, единицы информационного взаимодействия, единицы коммуникационного обмена, структурные информационные единицы.
На основе информационных единиц формируются составные информационные модели объекта и ситуации. Понятие ситуации и позиции используется широко. Например, ситуация и позиция в одном пространстве. Это может быть пространственная ситуация и пространственная позиция. Это может быть экономическая ситуация и экономическая позиция. Это может быть экологическая ситуации и экологическая позиция.
Возможны комбинации ситуаций и позиций. Например, пространственная ситуация и экономическая позиция. Другой пример, пространственная ситуация плюс экологическая ситуация плюс пространственная позиция и экономическая позиция. В целом такие комбинации создают основу пространственного ситуационного моделирования. Начальная информационная модель ситуации НИС имеет вид:
НИС = Ф{(Cр1,Cр2,…Cрn), (Тр1, Тр 2, … Тр m), (Аt1, At2, …Atk) (1)
Здесь Cpi — совокупность координатных пространственных параметров (i=1..n); Трi – совокупность параметров, зависящих от времени (i=1…m); Аti — совокупность тематических характеристик (i=1…k). Модель (1) открыта для включения дополнительных параметров.
Многоцелевое управление в неопределенных ситуациях
В процессе управления информационная ситуация может меняться и становится текущей информационной ситуацией. Текущая информационная модель ситуации ТИС имеет вид
ТИСj+1 = НИСj{(Cpij + ∆ Cр), (Трij +∆Тр), (Аtij +∆At) (2)
Здесь Cpij — совокупность координатных пространственных параметров на j-ом шаге управления; Трij – совокупность параметров, зависящих от времени на i-ом шаге управления; Аtij — совокупность тематических характеристик на i-ом шаге управления. В выражении (2) ∆ Cр, ∆Тр, ∆At – приращения параметров на очередном шаге управления. Степень изменения этих параметров может относить текущую информационную ситуацию к «белой», «серой» или «черной» (рис.2).
В сложных «серых» ситуациях возможна перемена локальной цели при сохранении стратегической и возможна даже замена стратегической цели. Это обусловлено изменчивостью текущей ситуации по отношению к запланированной ситуации. Изменчивость ситуации может переводить исходную «белую» информационную ситуацию в «серую» информационную ситуацию. Изменчивость ситуации переводит определенную первоначально информацию о текущей ситуации в неопределенную информацию (рис.1).
Например, в сфере транспорта изменением дорожной ситуации может повлечь изменение маршрута при сохранении конечной точки маршрута. Выбор цели, исходя из оперативной ситуации, означает также применение разных критериев оптимизации [32]. Например, при перевозке груза могут возникать следующие информационные ситуации с разными условиями решения оптимальной задачи:
Ситуация 1 критерий оптимальности — минимальное расстояние от точки погрузки до точки разгрузки (учет только стоимости перевозки без стоимости разгрузки);
Ситуация 2 критерий оптимальности — минимальное время доставки от начального пункта до пункта назначения (скорая помощь, доставка питания в детские учреждения);
Ситуация 3 критерий оптимальности — минимальная стоимость доставки с учетом погрузки и разгрузки (учет перевозки и стоимости погрузочно/разгрузочных работ);
Ситуация 4 критерий оптимальности — минимизация затрат на стоимость аренды одной из точек разгрузки (склада);
Ситуация 5 критерий оптимальности — минимизация риска при доставке особо ценного груза.
Ситуация 6 изменение начальных условий оптимальности вследствие изменения условий доставки или чрезвычайной ситуации. (например, авария, изменение конечного пункта доставки, выгрузка части груза на промежуточной станции).
Ситуации 1-6 являются основой для применения многоцелевого управления и для возникновения дополнительных задач управления. Ситуации 1-6 не исчерпывают возникновение дополнительных ситуаций, которые также требуют пространственного анализа. Возможны новые ситуации и комбинации из перечисленных ситуаций. В реальных условиях задачи доставки могут существенно меняться. Использование топологических моделей позволяет упрощать анализ пространственной ситуации. На рис.6 приведена простая ситуация доставки груза из точки 1 в точку 4.
Рис.6. Простой граф транспортной сети
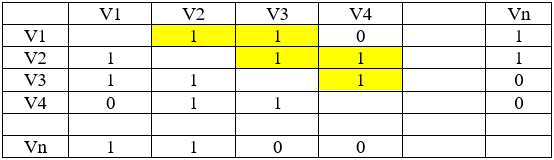
В таблице 3 приведена матрица пространственных отношений, инцидентная графу ситуации (рис.5) В таб.1 цифрой 1 отражена дуга между соответствующей вершиной Vi. Значение 0 означает отсутствие дуги (связи). В ситуации дорожного движения 0 означает невозможность прямого перемещения между этими пунктами.
Таблица 3 — Матрица пространственных отношений
Для определения маршрута из вершины V1 в вершину V4 отражена область соответствующих клеток матрицы. Граф (рис.6) определяет следующие комбинации маршрутов 124, 134, 1234 доставки их точки 1 в точку 4. Эти комбинации и есть решения в «серой» системе анализа. На основе матрицы пространственных отношений (таблица 1) строятся подобные матрицы для других пунктов отправления и назначения, которые служат основой для расчетов оптимальности прокладки маршрута.
Таблица 1 соответствует симметричным условиям, то есть одинаковым условиям движения в обе стороны. На практике имеют место ассиметричные ситуации с односторонним движением и ситуации с изменением трафика в течении дня.
Такие ситуации имеет место за счет разных типов дорог (главная, не главная) и условий движения. Кроме того, времена перемещения на вышерассмотренных маршрутах существенно меняются в зависимости от интервала движения в течение рабочего дня. Существует значительная зависимость длительности перевозки от времени в течение дня.
Это дает основание утверждать, что при перевозках нецелесообразно применять точечное оценивание времени, расстояния, и затрат. Точечным называется оценивание одной величины одной цифрой. На графике такому оцениванию соответствует точка. Вариабельность условий движения делает целесообразным применение для этой цели нечетких чисел, которые подразделяются на интервальные, треугольные и трапециевидные. Такой подход доказан в ряде работ [33, 34].
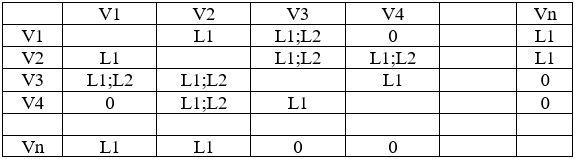
Серый анализ дает основание вводить разные матрицы оценки пространственной ситуации, например: матрицу временных отношений; матрицу расстояний; матрицу затрат. В таблице 4 приведена матрица расстояний или длин маршрутов (L). В ней использованы точечные значения (L1) и интервальные значения (L1, L2).
Таблица 4. Матрица расстояний маршрутов
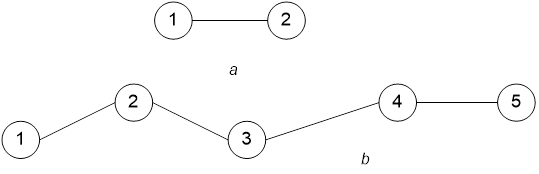
Это обусловлено тем, что для простых маршрутов, то есть для маршрутов между двумя вершинами графа или для маршрутов, которые описываются только одной линейной цепочкой, а не сетью, — длина маршрута величина постоянная. На рис.7 показаны примеры простых маршрутов.
Рис.7. Примеры простых маршрутов
На рисунке 7 для варианта а) изображено звено. На рисунке 7 b) дана линейная цепочка. Общим для таких маршрутов является постоянства длины маршрута. Это дает основание ввести определение простого маршрута как маршрута, длина L1 которого постоянна, а граф не имеет сетевой структуры.
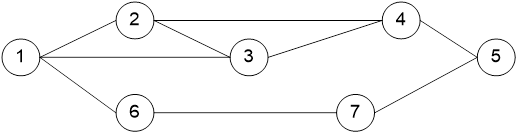
Длина сложного маршрута ( рис.8) длина задается интервалом L1;L2. Сложным будем назвать маршрут, который имеет сетевую структуру и , следовательно, при его реализации возможны комбинации, которые приводят к разным длинам маршрутов. На рис. 8 приведен пример (относительно) сложного маршрута. Пункт отправления вершина с номером 1, пункт назначения – вершина с номером 5.
Рис. 8. Сетевой граф с набором возможных маршрутов
Возможны следующие комбинации маршрутов (1245; 12345; 1345; 1675). Этот граф является упрощенной моделью городской ситуации. В случае стационарных условий движения, выбирают маршрут, отвечающий условиям оптимальности. Но в случае изменения ситуации, оптимальный маршрут может быть любым. Поэтому в общем случае длина маршрута будет иметь столько значений, сколько существует возможных комбинаций маршрута их начальной точки в конечную. В нашем случае каждый возможный маршрут имеет частную длину
l1= Length of route(1245);
l2= Length of route(12345);
l3= Length of route(1345);
l4= Length of route(1675).
Эти значения частных длин задают интервал минимальной L1 и максимальной L2 длины маршрута
L1=min [l1= Length of route(1245); l2= Length of route(12345); l3= Length of route(1345); l4= Length of route(1675)]
L2=maxn [l1= Length of route(1245); l2= Length of route(12345); l3= Length of route(1345); l4= Length of route(1675)]
Любые значения длин маршрутов лежат внутри этого интервала. Таким образом, матрица приведенная в таблице 2, включает точечные и нечеткие (интервальные) значения. Следует также подчеркнуть, что матрица пространственных отношений (таблица 1) является родовидовой для этой и других матриц оценки маршрутов. Следующая матрица оценки маршрутов – это матрица временных отношений, которая приведена в таблице 5.
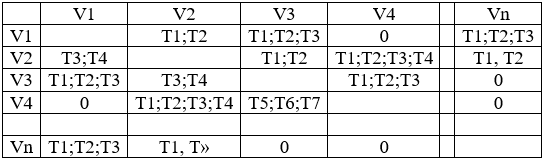
Таблица 5 — Матрица временных отношений
Матрица временных отношений показывает время перемещения из одной вершины в другую, а общее время движения по маршруту определяется совокупностью времен звеньев, входящих в маршрут. Как отмечено выше, время движения может различаться в зависимости от направления движения, даже в том случае, когда длина маршрута неизменна. Кроме того, на время движения влияет время суток, что связано с загруженностью трасс. Все это обуславливает введение: интервальных (T1, T2). Треугольных (Т1, Т2, Т3) и трапециевидных (Т1, Т2, Т3, Т4) — чисел для оценки времени перемещения.
Кроме того, матрица временных отношений (таблица 3) может быть ассиметричной. Это обусловлено тем, что время движения по обратному маршруту не равно движению времени по прямому маршруту, даже при неизменной длине маршрута в прямом и обратном направлении. Это обстоятельство отражено в таблице 3 тем, что отношение между вершинами V2-V3 в одну сторону задается интервалом Т1,Т2, а в другую V3-V2 отношением Т3,Т4. Асимметрия имеет место и в отношении вершин V3-V4. В дну сторону оно отражается треугольным числом Т1, Т2, Т3, а в другую треугольным числом Т5, Т6, Т7.
Однако важно отметить качественное соответствие чисел. Если в одну сторону дается интервальная оценка, то и в другую сторону эта оценка тоже будет интервальной. Если в одну сторону дается треугольная оценка, то и в другую сторону эта оценка тоже будет треугольной. Если в одну сторону дается трапециевидная оценка, то и в другую сторону эта оценка тоже будет трапециевидной. Общий вывод для временных отношений имеет место симметрия по качественной характеристики и возможная асимметрия по количественной характеристике.
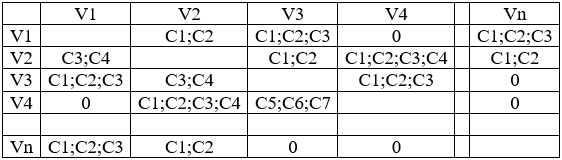
В таблице 4 приведена матрица затрат. Это наиболее сложный показатель, но в качественном плане он близок к матрице временных отношений, поскольку эта характеристика более вариабельна и эту вариабельность она накладывает на характер затрат. Еще раз напомним, что родовидовой для матрицы затрат (таблица 6) является матрица пространственных отношений.
Таблица 6 — Матрица затрат
В таблицах 2-4 одно значение является точечным, два значения (С1, С2) являются прямоугольным числом, три значения (С1,С2, С3) обозначают треугольное число, четыре значения (С1, С2, С3, С4) обозначают трапециевидное число.
Возникает вопрос оценки характеристик маршрута по данным таблиц 2, 3, 4. Это представляет определенные трудности, поскольку обработка нечетких чисел отличается от обработки обычных чисел и требует определенной подготовки. Тем не менее, в настоящее время накоплен достаточный опыт [35], позволяющий решать данные задачи. Следует также отметить, что, при использовании нечетких множеств, широко используют нечеткие графы [24]. Следующим шагом является выбор оптимальных величин таблиц 2 – 4. После этого используют методы теории предпочтений [26] для выбора оптимального маршрута.
Таким образом, «серая» оценка характеристик маршрута лежит в области нечетких чисел и практически исключает обычный анализ, использующий точечные величины. Применение описанной методики позволяет адекватно оценивать характеристики маршрутов в условиях современного движения со сложной меняющейся обстановкой и асимметричными характеристиками движения.
Выводы
Управление в условиях неопределенности имеет множество вариантов реализации и его нельзя сводить только к одному методу. Серый пространственный анализ является относительно новым методов, неизвестным широкому кругу управленцев. Серый пространственный анализ в отдельных случаях дополняет теорию нечетких множеств, в других случаях самостоятельно решает задачи поддержки принятия решений. Серый пространственный ситуационный анализ включает три принципа. 1) определение пространственных отношений как основы моделирования и развития ситуаций. 2) определение модели микросреды, которая влияет на ситуацию. 3) определение модели объекта с учетом связей и отношений с микросредой и макросредой. Методы серого пространственного анализа допускают задание нескольких критериев оптимальности и решение нескольких задач управления, с учетом возможного изменения ситуации и возможного перехода от одной задачи управления к другой. Техника серого пространственного анализа требует анализа ситуации и перехода от точечных значений параметров к интервальным, треугольным или трапециевидным значениям. В соответствии с этим решение задач будет множественным, а не единичным как при точечных оценках параметров.
Серый пространственный анализ создает в итоге адекватное описание сложной ситуации, новые информационные ресурсы и новые знания. Он позволяет решать широкий круг задач, который с помощью иных методов моделирования решить нельзя Особое значение этого анализа в том, что он используется при поддержке принятия решений, при управлении подвижными объектами и при многоцелевом управлении. Серый пространственный анализ допускает использование когнитивного управления с применением когнитивных карт и методов когнитивного моделирования.
Читайте также
Библиографический список
- Демидова Л. А., Кираковский В. В., Пылькин А. Н. Принятие решений в условиях неопределенности. — М.: Горячая линия — Телеком, 2015. — 283 с.
- Розенберг И.Н., Старостина Т.А. Решение задач размещения с нечеткими данными с использованием геоинформационных систем. — М. Научный мир, 2006. — 208с
- Боженюк А.В., Герасименко Е.М., Розенберг И.Н. Определение потока минимальной стоимости в нечетком динамическом графе//Известия ЮФУ. Технические науки. -2013. -№ 5 (142). -C. 149-154
- Боженюк А.В., Розенберг И.Н. Метод размещения центров обслуживания на интервальных графах. // Известия ТРТУ. — 2006, — №9 (64). – с.141-145.
- Feng, L. (1997). Research on the Identification Coefficient of Relational Grade for Grey System [J].Systems Engineering—Theory & Practice,6
- Chan WK and Tong TKL, (2007), Multi-criteria material selections and end-of-life product strategy: Grey relational analysis approach, Materials & Design, Volume 28, Issue 5, Pages 1539-1546.
- Цветков В.Я. Серый реляционный анализ // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 12-1. – с166-166.
- Liu G., Yu J. Gray correlation analysis and prediction models of living refuse generation in Shanghai city //Waste Management. – 2007. – Т. 27. – №. 3. – С. 345-351
- Yufeng G., Jing W., Zidian H. Gray correlation analysis on influencing factors of postgraduates’ innovative capacity //Journal of Theoretical and Applied Information Technology. – 2013. – V. 49. – №. 1. – p.419-425.
- Tsvetkov V. Ya. Framework of Correlative Analysis // European researcher. Series A. 2012. № 6-1 (23). С. 839-844.
- Theil H. The information approach to demand analysis //Econometrica: Journal of the Econometric Society. – 1965. – р.67-87.
- Неймарк Ю. И., Стронгин Р. Г. Информационный подход к задаче поиска экстремума функций. //Изв. АНСССР. Техн. кибернетика. – 1966. – №. 1. – С. 17-26.
- Цветков В.Я., Корнаков А.Н. Информационный подход в управлении // Успехи современного естествознания. — 2010. — №3. – c.137-138.
- Цветков В.Я. Информационный подход // Международный журнал прикладных и фундаментальных исследований. — 2016. — 4- 3. – с.645-645
- Шайтура С.В. Информационная ситуация в геоинформатике// Образовательные ресурсы и технологии. – 2016. — №5 (17). – с.103-108.
- Цветков В.Я. Информационные модели объектов, процессов и ситуаций// Дистанционное и виртуальное обучение– 2014. — №5. — с.4- 11
- Ожерельева Т.А. Информационная ситуация как инструмент управления // Славянский форум, 2016. -4(14). – с.176-181
- Розенберг И.Н., Цветков В.Я. Информационная ситуация. // Международный журнал прикладных и фундаментальных исследований. — 2010. — 12. — с.126-127
- Павлов А.И. Пространственная информационная ситуация // Славянский форум, 2016. -4(14). – с.198-203
- Цветков В.Я. Информационная неопределенность и определенность в науках об информации // Информационные технологии. — 2015. — №1. -с.3-7.
- Горелова Г.В., Захарова Е.Н., Гинис Л.А. Когнитивный анализ и моделирование устойчивого развития социально-экономических систем — Ростов н/Д: Изд-во Рост. ун-та, 2005. — 288 с.
- Номоконов И.Б. Когнитивные методы при лучевой диагностике. Монография — М.: МАКС Пресс , 2016. — 60с.
- Розенберг И.Н. Интеллектуальное управление// Современные технологии управления. 2017. — №4 (76). – с.45-50.
- Цветков В. Я. Ситуационное моделирование в геоинформатике // Информационные технологии. – 2014. — №6. – с.64-69.
- Pospelov D. А. Situational Management: Theory and Practice //Мoscow: Nauka (in Russian). – 1986.
- Chapman S. L., Jeffrey D. B. Situational management, standard setting, and self-reward in a behavior modification weight loss program //Journal of consulting and clinical psychology. – 1978. – V.46. – №. 6. – p.1588.
- Mayer J. H., Winter R., Mohr T. Situational management support systems //Business & Information Systems Engineering. – 2012. – V. 4. – №. 6. – p.331-345.
- V. P. Savinykh and V. Ya. Tsvetkov. Geodata As a Systemic Information Resource. Herald of the Russian Academy of Sciences, 2014, Vol. 84, No. 5, pp. 365–368. DOI: 10.1134/S1019331614050049
- V. Ya. Tsvetkov. Information Relations // Modeling of Artificial Intelligence, 2015, Vol.(8), Is. 4. – р.252-260. DOI: 10.13187/mai.2015.8.252 www.ejournal11.com.
- Сигов А. С., Цветков В.Я. Неявное знание: оппозиционный логический анализ и типологизация // Вестник Российской Академии Наук, 2015, том 85, № 9, — с.800–804. DOI: 10.7868/S0869587315080319.
- Encyclopedia of Management http://www.enotes.com/management-encyclopedia/management-thought. Дата доступа 5.06.2017.
- 3 V. Ya. Tsvetkov. Multipurpose Management// European Journal of Economic Studies 2012, Vol.(2), № 2 р.140-143.
- Розенберг И.Н., Старостина Т.А. Минимаксная задача размещения обслуживающих пунктов в нечетких условиях // Системы и средства информатики. Спецвыпуск №2. «Математические методы в информатике». Издательство ИПИ РАН, Москва, 2002, с.206-219.
- Розенберг И.Н., Старостина T.A. Решение задач пространственной оптимизации // Системы и средства информатики. Специальный выпуск «Геоинформационные технологии»/ Под ред. И.А. Соколова. Москва: ИПИ РАН, 2004. – с. 213-231.
- Берштейн Л.С., Боженюк А.В. Нечеткие графы и гиперграфы. М.: Научный мир, 2005. – 256с.
References
- Demidova L. A., Kirakovskij V. V., Pyl’kin A. N. Decision-making under uncertainty [Prinjatie reshenij v uslovijah neopredelennosti]. – Moscow: Hot line – Telecom, 2015. – 283 p.
- Rozenberg I.N., Starostina T.A. Solution of allocation problems with fuzzy data using geoinformation systems [Reshenie zadach razmeshhenija s nechetkimi dannymi s ispol’zovaniem geoinformacionnyh sistem]. – M. Scientific world, 2006. – 208s
- Bozhenjuk A.V., Gerasimenko E.M., Rozenberg I.N. Determination of the minimum value flow in a fuzzy dynamic graph. [Opredelenie potoka minimal’noj stoimosti v nechetkom dinamicheskom grafe]// Izvestiya SFU. Technical science. -2013. -No 5 (142). -C. 149-154
- Bozhenjuk A.V., Rozenberg I.N. The method of locating service centers on interval graphs [Metod razmeshhenija centrov obsluzhivanija na interval’nyh grafah] // Proceedings of TSURE. – 2006, – No. 9 (64). – p.141-145.
- Feng, L. (1997). Research on the Identification Coefficient of Relational Grade for Grey System [J].Systems Engineering—Theory & Practice,6
- Chan WK and Tong TKL, (2007), Multi-criteria material selections and end-of-life product strategy: Grey relational analysis approach, Materials & Design, Volume 28, Issue 5, Pages 1539-1546.
- Cvetkov V.Ja. Gray relational analysis [Seryj reljacionnyj analiz]// International Journal of Applied and Fundamental Research. – 2016. – No. 12-1. – p166-166.
- Liu G., Yu J. Gray correlation analysis and prediction models of living refuse generation in Shanghai city //Waste Management. – 2007. – Т. 27. – №. 3. – С. 345-351
- Yufeng G., Jing W., Zidian H. Gray correlation analysis on influencing factors of postgraduates’ innovative capacity //Journal of Theoretical and Applied Information Technology. – 2013. – V. 49. – №. 1. – p.419-425.
- Tsvetkov V. Ya. Framework of Correlative Analysis // European researcher. Series A. 2012. № 6-1 (23). С. 839-844.
- Theil H. The information approach to demand analysis //Econometrica: Journal of the Econometric Society. – 1965. – р.67-87.
- Nejmark Ju. I., Strongin R. G. Information approach to the problem of finding the extremum of functions [Informacionnyj podhod k zadache poiska jekstremuma funkcij] // Izv. ANSSSR. Techn. cybernetics. – 1966. – No. 1. – P. 17-26.
- Cvetkov V.Ja., Kornakov A.N. Information approach in management [Informacionnyj podhod v upravlenii]// Successes of modern natural science. – 2010. – №3. – c.137-138.
- Cvetkov V.Ja. Information approach [Informacionnyj podhod]// International Journal of Applied and Fundamental Research. – 2016. – 4- 3. – p.645-645
- Shajtura S.V. Information situation in geoinformatics [Informacionnaja situacija v geoinformatike]// Educational resources and technologies. – 2016. – No. 5 (17). – p.103-108.
- Cvetkov V.Ja. Information models of objects, processes and situations [Informacionnye modeli ob#ektov, processov i situacij]// Remote and virtual training- 2014. – №5. – p.4-11
- Ozherel’eva T.A. Information situation as a management tool [Informacionnaja situacija kak instrument upravlenija]// Slavic Forum, 2016. -4 (14). – p.176-181
- Rozenberg I.N., Cvetkov V.Ja. Information situation [Informacionnaja situacija] // International Journal of Applied and Fundamental Research. – 2010. – 12. – p.126-127
- Pavlov A.I. Spatial information situation [Prostranstvennaja informacionnaja situacija]// Slavic Forum, 2016. -4 (14). – p.198-203
- Cvetkov V.Ja. Information Uncertainty and Certainty in the Sciences of Information [Informacionnaja neopredelennost’ i opredelennost’ v naukah ob informacii]// Information Technologies. – 2015. – №1. -c.3-7.
- Gorelova G.V., Zaharova E.N., Ginis L.A. Cognitive analysis and modeling of sustainable development of socio-economic systems [Kognitivnyj analiz i modelirovanie ustojchivogo razvitija social’no-jekonomicheskih sistem] – Rostov n / a: Izd-vo Rost. University, 2005. – 288 p.
- Nomokonov I.B. Cognitive methods in radiation diagnosis. Monograph [Kognitivnye metody pri luchevoj diagnostike] – Moscow: MAX Press, 2016. – 60s.
- Rozenberg I.N. Intellectual management [Intellektual’noe upravlenie]// Modern management technologies. 2017. -? 4 (76). – p.45-50.
- Cvetkov V. Ja. Situational modeling in geoinformatics [Situacionnoe modelirovanie v geoinformatike]/ / Information technology. – 2014. – №6. – p.64-69.
- Pospelov D. А. Situational Management: Theory and Practice //Мoscow: Nauka (in Russian). – 1986.
- Chapman S. L., Jeffrey D. B. Situational management, standard setting, and self-reward in a behavior modification weight loss program //Journal of consulting and clinical psychology. – 1978. – V.46. – №. 6. – p.1588.
- Mayer J. H., Winter R., Mohr T. Situational management support systems //Business & Information Systems Engineering. – 2012. – V. 4. – №. 6. – p.331-345.
- V. P. Savinykh and V. Ya. Tsvetkov. Geodata As a Systemic Information Resource. Herald of the Russian Academy of Sciences, 2014, Vol. 84, No. 5, pp. 365–368. DOI: 10.1134/S1019331614050049
- V. Ya. Tsvetkov. Information Relations // Modeling of Artificial Intelligence, 2015, Vol.(8), Is. 4. – р.252-260. DOI: 10.13187/mai.2015.8.252 www.ejournal11.com.
- Sigov AS, Tsvetkov V.Ya. Implicit knowledge: opposition logical analysis and typology [Implicit knowledge: oppositional logical analysis and typology]// Bulletin of the Russian Academy of Sciences, 2015, volume 85, No. 9, p.800-804. DOI: 10.7868 / S0869587315080319.
- Encyclopedia of Management http://www.enotes.com/management-encyclopedia/management-thought. Дата доступа 5.06.2017.
- 3 V. Ya. Tsvetkov. Multipurpose Management// European Journal of Economic Studies 2012, Vol.(2), № 2 р.140-143.
- Rozenberg I.N., Starostina T.A. Minimax task of placing service points in fuzzy conditions [Minimaksnaja zadacha razmeshhenija obsluzhivajushhih punktov v nechetkih uslovijah]// Systems and means of informatics. Special issue number 2. “Mathematical methods in computer science”. Publishing house IPI RAS, Moscow, 2002, p.206-219.
- Rozenberg I.N., Starostina T.A. Solving the problems of spatial optimization [Reshenie zadach prostranstvennoj optimizacii]// Systems and Means of Informatics. Special issue of “Geoinformation technologies” / Ed. I.A. Sokolov. Moscow: IPI RAS, 2004. – p. 213-231.
- Bershtejn L.S., Bozhenjuk A.V. Fuzzy graphs and hypergraphs [Nechetkie grafy i gipergrafy]. М .: the Scientific world, 2005. – 256с.