Индексный подход к анализу территориального распределения и динамики затратных показателей российской инновационной системы

Авторы
Аннотация
В статье автор рассматривает вопрос концентрации затратных показателей российской инновационной системы, применив индексный метод. Эмпирической базой исследования служили статистические данные, в качестве инструментария использовался пакет анализа данных общественных наук SPSS Base. Объектами исследования послужили федеральные округа, а также крупные научные центры – г. Москва и г. Санкт-Петербург, по состоянию на 2000-2009 гг.
Ключевые слова
территориальные индексы, временные сравнения, МНК-оценки линейных моделей, аппроксимация трендов временных рядов, затратные показатели, технологические инновации.
Рекомендуемая ссылка
No items found. Индексный подход к анализу территориального распределения и динамики затратных показателей российской инновационной системы // Современные технологии управления. ISSN 2226-9339. — №3 (15). Номер статьи: 1503. Дата публикации: 08.03.2012. Режим доступа: https://sovman.ru/article/1503/
Authors
Abstract
Keywords
Suggested citation
No items found. // Modern Management Technology. ISSN 2226-9339. — №3 (15). Art. # 1503. Date issued: 08.03.2012. Available at: https://sovman.ru/article/1503/
В нашей предыдущей публикации [1] рассматривалось распределение по федеральным округам РФ и крупным научным центрам основных затратных показателей – внутренних затрат на научные исследования и разработки и затрат на технологические инновации. Был выявлен высокий уровень концентрации внутренних затрат на научные исследования и разработки в крупных научных центрах. Так, в лидере – Москве на душу населения приходилось внутренних затрат на научные исследования и разработки на душу населения больше, чем в аутсайдере – ЮФО, в 10,2 и 11,7 раз в 2000 и 2009 гг. соответственно. С затратами на технологические инновации сложилась иная ситуация: если в 2000 г. первое место по уровню удельных затрат на технологические инновации занимала Москва, то в 2009 г. – Дальневосточный федеральный округ, тогда как в Москве затраты на душу населения стали даже меньше среднероссийского уровня. При этом концентрация затрат на технологические инновации со временем заметно уменьшилась.
Рассмотрим вопрос концентрации затратных показателей российской инновационной системы более детально, применив индексный метод. Как и в работе [1], эмпирической базой исследования служили статистические данные источника [2], в качестве инструментария использовался пакет анализа данных общественных наук SPSS Base [3]. Объектами исследования являлись федеральные округа, а также крупные научные центры – г. Москва и г. Санкт-Петербург, по состоянию на 2000-2009 гг.
Нами отмечалось [1], что использование индексного метода, в соответствии с которым анализу подлежат не абсолютные показатели, а территориальные индексы, рассчитываемые как отношения величины показателя в данной территории к его значению в РФ в целом, позволяет проводить временные сравнения. При этом эффективным способом временных сравнений является представление распределения по федеральным округам и крупным научным центрам территориальных индексов внутренних затрат на научные исследования и разработки, а также затрат на технологические инновации, в виде территориальных профилей показателей, представленных на рис. 1.
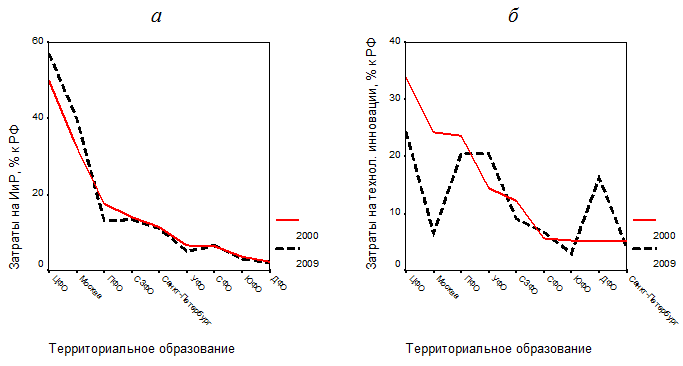
Рис. 1. Территориальные профили затратных показателей российской инновационной системы: а – внутренние затраты на научные исследования и разработки; б – затраты на технологические инновации
Поясним порядок построения территориальных профилей. Вначале исследуемые статистические объекты ранжируются по убыванию показателей для года, принятого в качестве базового (в данном случае, 2000 г.). Затем строятся два или более графика последовательности по данным для различных временных моментов (интервалов).
Предварительное ранжирование позволяет наглядно выявить изменения в ранжировании статистических объектов. Так, на диаграмме рис. 1 а хорошо видно, что лидером по внутренним затратам на научные исследования и разработки и в 2000, и в 2009 гг. был Центральный федеральный округ, второе место принадлежало Москве, не изменились и аутсайдеры – Дальневосточный, Южный и Сибирский федеральные округа. Иная картина наблюдается в отношении затрат на технологические инновации (рис. 1 б): хотя лидер здесь остался неизменным – Центральный федеральный округ, Москва, которая в 2000 г. занимала второе место по данному виду затрат, уступала это место Приволжскому федеральному округу, став, наряду с Южным федеральным округом и Санкт-Петербургом, аутсайдером.
В нашей предыдущей работе [1] было выполнено сравнение уровня удельных затрат на технологические инновации с затратами на исследования и разработки, в расчете на душу населения. При этом по данным за 2000 г. просматривалась положительная корреляция удельных затрат на технологические инновации с затратами на исследования и разработки, а данным за 2009 г. такая корреляция отсутствовала.
Аналогичное исследование выполнено нами и для территориальных индексов – рис. 2.
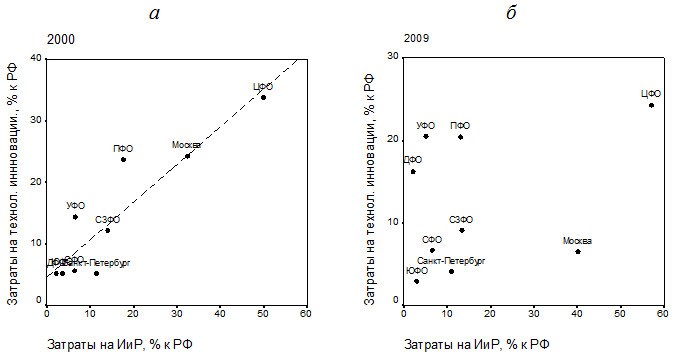
Рис. 2. Соотношение территориальных индексов затрат на технологические инновации и затрат на исследования и разработки: а – в 2000 г.; б – в 2009 г.
По расположению меток территориальных образований РФ на диаграмме рис. 2 б можно выделить четыре их типа. Первый тип, к которому относятся Южный, Сибирский и Северо-Западный федеральные округа, а также г. Санкт-Петербург, характеризуется пониженными значениями территориальных индексов обоих затрат. Ко второму типу территориальных образований относятся Приволжский, Уральский и Дальневосточный федеральные округа. В этих федеральных округах уровень затрат на технологические инновации выше, чем на исследования и разработки. Центральный федеральный округ относится к третьему типу территориальных образований, это – безусловный лидер по затратам и на исследования и разработки, и на технологические инновации. Четвертый тип территориальных образований – г. Москва – характеризуется высоким уровнем затрат на исследования и разработки, и низким – на технологические инновации.
Для уточнения отнесения территориальных образований к этим трем типам нами выполнен иерархический кластерный анализ по методу Уорда с квадратичной евклидовой метрикой на территориальных индексах. Как отмечалось в нашей предыдущей работе [1], этот метод, как правило, приводит к образованию кластеров примерно равного размера [4], использование квадратичной евклидовой метрики повышает «контрастность» дендрограммы – основного результата иерархического кластерного анализа [5], а в z-преобразовании в данном случае нет необходимости: оба территориальных индекса безразмерны (выражены в процентах).
По дендрограмме, отражающей последовательность объединения территориальных образований в однородные группы по видам удельных затрат – кластеры, на уровне их сходства 90% можно выделить четыре кластера (рис. 3). В первый входит один федеральный округ – ЦФО, во второй – г. Москва, в третий – ПФО, УФО и ДФО, в четвертый – СЗФО, СФО и ЮФО, а также г. Санкт-Петербург.

Рис. 3. Дендрограмма кластерного анализа территориальных образований РФ по индексам затрат на инновации (метод Уорда, квадратичная евклидова метрика)
Для проверки устойчивости четырехкластерного решения, полученного в результате иерархического кластерного анализа, нами выполнен итеративный кластерный анализ, который полностью подтвердил указанное выше отнесение территориальных образований к выделенным кластерам (табл. 1).
Таблица 1
Сопоставление отнесения территориальных образований РФ к кластерам по двум методам кластерного анализа
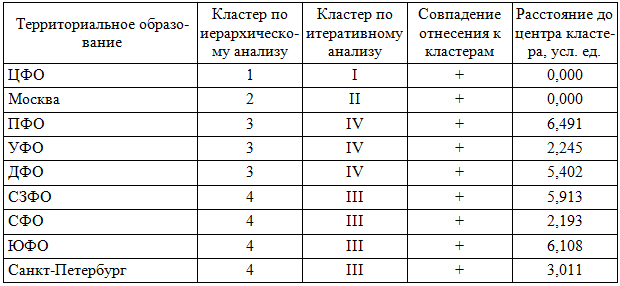
Ящичковые диаграммы, представленные на рис. 4, иллюстрируют выполненную нами выше идентификацию кластеров.
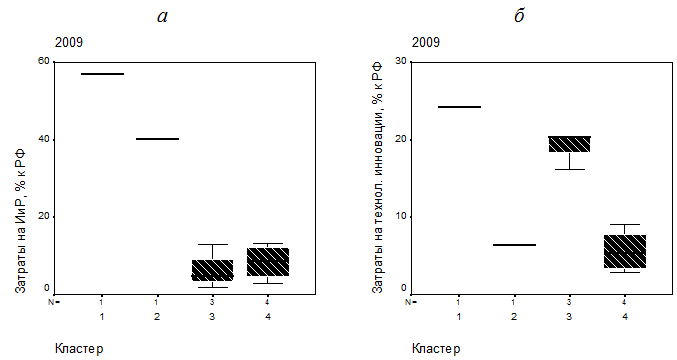
Рис. 4. Распределение территориальных индексов затрат по кластерам территориальных образований: а – на исследования и разработки; б – на технологические инновации
Перейдем теперь к анализу динамики территориальных индексов затратных показателей российской инновационной системы. Здесь нами принята следующая технология: вначале строили графики временных рядов для всех включенных в анализ территориальных образований, затем с помощью процедуры «Curve Estimation» рассчитывали параметры линейных моделей, аппроксимирующих тренды временных рядов. При этом выяснилось, что на линейные тренды временных рядов территориальных индексов затратных показателей для большинства территориальных образований накладываются значительная по величине стохастическая составляющая, и лишь в некоторых случаях удалось получить адекватные модели. Тем не менее, такой подход оправдан, поскольку в этом случае мы получаем МНК-оценки средних характеристик временных рядов, принятые в теории статистики: средний уровень территориального индекса и среднегодовой его прирост.
Сказанное иллюстрируют рис. 5 и 6.
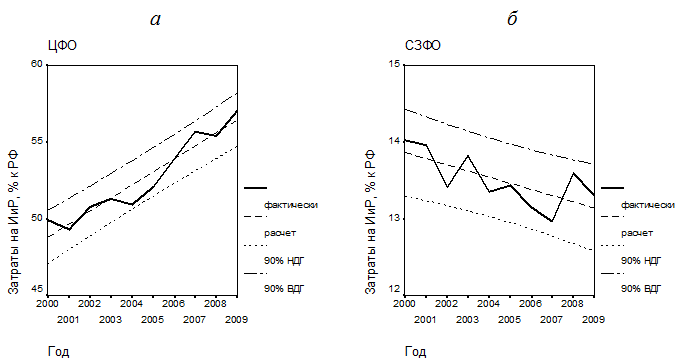
Рис. 5. Аппроксимация динамики территориальных индексов затрат на научные исследования и разработки: а – Центральный федеральный округ; б – Северо-Западный федеральный округ
Как видно из графиков рис. 5, построенных для Центрального и Северо-Западного федеральных округов, если динамика территориального индекса затрат на исследования и разработки в ЦФО носит нарастающий характер, то динамика этого территориального индекса в СЗФО носит убывающий характер. На линейные тренды в обоих случаях накладывается стохастическая составляющая – меньшая для Центрального федерального округа, большая – для Северо-Западного федерального округа. Тем не менее, для обоих федеральных округов получены вполне приемлемые линейные модели:
— для ЦФО
Wзатр_ИиР = 52,62 + 0,85 t; (1)
— для СЗФО
Wзатр_ИиР = 13,50 – 0,08 t, (2)
где t – временная переменная, определяемая соотношением
t = год – 2004,5. (3)
При таком назначении временной переменной содержательный смысл свободного коэффициента – это среднее за период 2000-2009 гг. значение территориального индекса затрат на исследования и разработки, коэффициента регрессии – среднегодовой прирост территориального индекса. Размерность обоих параметров линейных моделей – проценты.
Модель (1) оказалась адекватной эмпирическим данным: коэффициент детерминации R2=0,919; критерий Фишера F=91,3 статистически значим на р-уровне не хуже 0,00005. Модель (2) менее точная: она объясняет чуть меньше половины общей дисперсии (R2=0,491), однако критерий Фишера F=7,7 статистически значим на достаточно высоком уровне р=0,0240.
Временные ряды территориальных индексов затрат на технологические инновации в еще большей степени подвержены влиянию стохастической составляющей, что проявляется в большой ширине 90%-х доверительных интервалов на графиках рис. 6.
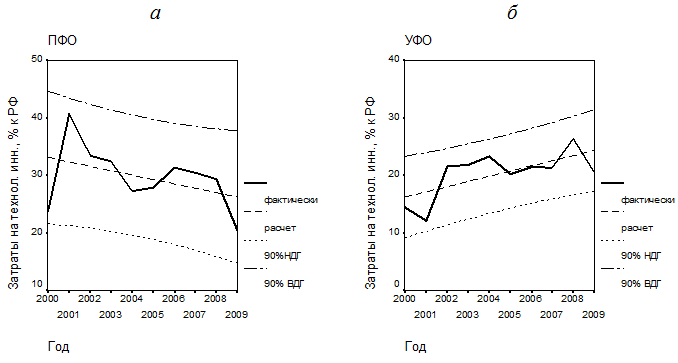
Рис. 6. Аппроксимация динамики территориальных индексов затрат на технологические инновации: а – Приволжский федеральный округ; б – Уральский федеральный округ
Результаты аппроксимации динамики территориальных индексов затратных показателей в период 2000-2009 гг. сведены в табл. 2; для сокращения объема публикации в ней приведены значения лишь одной характеристики качества линейных моделей – коэффициента детерминации.
Таблица 2
Параметры динамики территориальных индексов затратных показателей
|
Территориальное образование |
Затраты на научные исследования и разработки |
Затраты на технологические инновации |
||||
|
Средний уровень индекса, % к РФ |
Среднегодовой прирост индекса, % |
Коэффициент детерминации |
Средний уровень индекса, % к РФ |
Среднегодовой прирост индекса, % |
Коэффициент детерминации |
|
| ЦФО |
52,62 |
0,850 |
0,919 |
22,77 |
-0,492 |
0,113 |
| Москва |
35,76 |
0,866 |
0,953 |
9,46 |
-1,079 |
0,321 |
| СЗФО |
13,50 |
-0,080 |
0,491 |
10,70 |
-0,112 |
0,043 |
| Санкт-Петербург |
11,08 |
-0,019 |
0,042 |
4,71 |
-0,022 |
0,004 |
| ЮФО |
3,29 |
-0,025 |
0,207 |
5,15 |
0,022 |
0,003 |
| ПФО |
15,89 |
-0,589 |
0,866 |
29,63 |
-0,767 |
0,175 |
| УФО |
6,03 |
-0,154 |
0,862 |
20,26 |
0,902 |
0,435 |
| СФО |
6,52 |
0,007 |
0,026 |
6,84 |
0,225 |
0,253 |
| ДФО |
2,15 |
-0,010 |
0,099 |
4,65 |
0,222 |
0,022 |
Анализируя данные, приведенные в табл. 2, можно заметить, что среднегодовой прирост индекса затрат на исследования и разработки коррелирует с его средним уровнем – рис. 7.
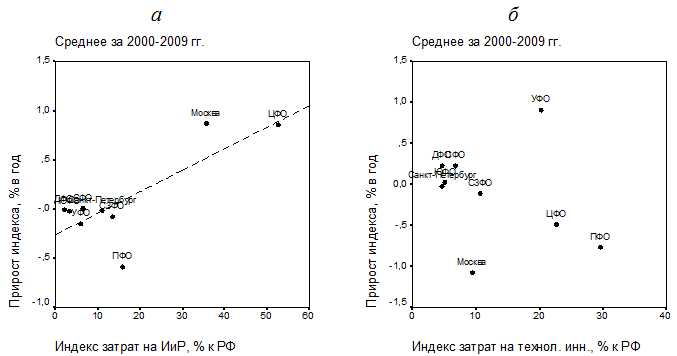
Рис. 6. Взаимосвязь параметров динамики территориальных индексов: затрат на технологические инновации: а – затраты на научные исследования и разработки; б – затраты на технологические инновации
Наличие данной корреляции обусловило реализацию факторного анализа с целью выявления структуры совокупности параметров моделей динамики территориальных индексов затратных показателей. Однако вначале выполним корреляционный анализ. Для краткости дальнейшего изложения ведем обозначения:
— х1 – средний уровень территориального индекса затрат на научные исследования и разработки;
— х2 – среднегодовой прирост индекса затрат на научные исследования и разработки;
— х3 – средний уровень территориального индекса затрат на технологические инновации;
— х4 – среднегодовой прирост индекса затрат на технологические инновации.
Результаты корреляционного анализа приведены в табл. 3.
Таблица 3
Корреляционная матрица параметров динамики территориальных индексов затратных показателей
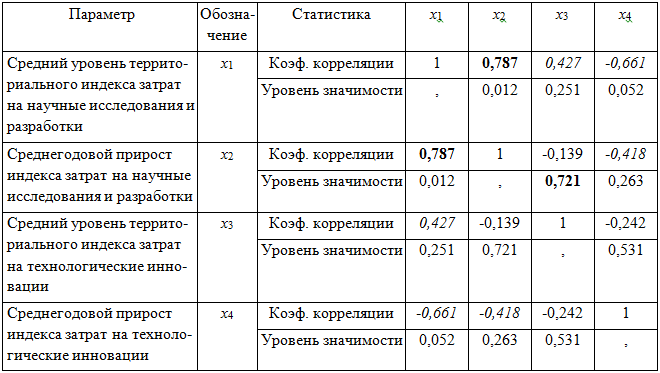
Из табл. 3 следует, что между параметрами х1 … х4 по выборке территориальных образований объемом N=9 имеются статистически значимые линейные корреляции сильной и средней силы (выделены полужирным шрифтом и курсивом соответственно), и это позволяет рассчитывать на успешные результаты факторного анализа.
Действительно, в результате факторного анализа, выполненного в программной среде пакета статистического анализа данных общественных наук SPSS Base по методу главных компонент с вращением главных факторов по критерию «варимакс» [6], адекватной оказалась двухфакторная модель, объясняющая 86,4% общей дисперсии – табл. 4.
Таблица 4
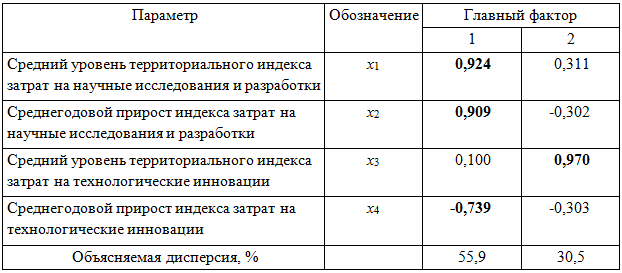
Корреляции параметров динамики территориальных индексов затратных показателей с главными факторами
Геометрические искажения при переходе от исходного множества из четырех параметров динамики территориальных индексов затратных показателей меньше критического значения 15% [7], и это позволяет выполнить интерпретацию главных факторов.
Главный фактор F1 – более информативный, он объясняет 55,9% общей дисперсии. Он положительно и сильно коррелирует с двумя параметрами динамики затратных показателей: средним уровнем территориального индекса затрат на научные исследования и разработки и среднегодовым приростом этого индекса с коэффициентами корреляции 0,924 и 0,909 соответственно, и отрицательно – со среднегодовым приростом индекса затрат на технологические инновации. На этом основании первый главный фактор можно квалифицировать как фактор уровня и роста затрат на научные исследования и разработки.
Второй главный фактор F2 положительно и сильно коррелирует с одним параметром – средним уровнем территориального индекса затрат на технологические инновации (коэффициент корреляции R=0,970), что позволяет его квалифицировать как фактор уровня затрат на технологические инновации. Этот главный фактор менее информативен, он объясняет 30,5% общей дисперсии.
Рис. 7 иллюстрирует отмеченные корреляции.
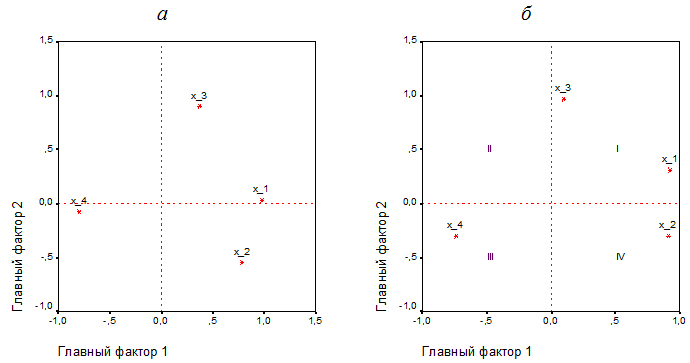
Рис. 7. Корреляция параметров динамики территориальных индексов затратных показателей с главными факторами: а – до их вращения; б – после вращения
Для лучшего понимания факторной структуры множества параметров динамики территориальных индексов затратных показателей на рис. 7 представлены диаграммы нагрузок на главные факторы до и после их вращения. Из сравнения диаграмм этого рисунка следует, что в результате вращения главных факторов по критерию «варимакс» структура факторного пространства существенно улучшилась, главные факторы стали более «ортогональны».
Главных факторов – два, и имеется возможность наглядно представить не только факторную структуру параметров динамики территориальных индексов затратных показателей, но и размещение территориальных образований на плоскости главных факторов, а также выполнить интерпретацию этого размещения. Так, квадрант I – это область, отвечающая повышенным значениям уровня и роста затрат на научные исследования и разработки, а также уровня затрат на технологические инновации, тогда как квадрант III – область, отвечающая пониженным значениям обоих факторов. Расположение территориальных образований в квадранте IV отвечает повышенным значениям уровня и роста затрат на научные исследования и разработки и пониженным – уровня затрат на технологические инновации. Диаметрально противоположное расположение территориальных образований в квадранте II отвечает области пониженных значений уровня и роста затрат на научные исследования и разработки и повышенного уровня затрат на технологические инновации.
На диаграммах рис. 8 представлено размещение территориальных образований по состоянию в 2000-2009 гг. Видно, в частности, что Центральный федеральный округ на диаграмме находится в квадранте I – квадранте с повышенными значениями и уровня и роста затрат на научные исследования и разработки, и уровня затрат на технологические инновации. Приволжский же федеральный округ на диаграмме расположен в квадранте II, и он характеризуется пониженными значениями уровня и роста затрат на научные исследования и разработки, а также повышенным уровнем затрат на технологические инновации.
Эти примеры можно продолжить.
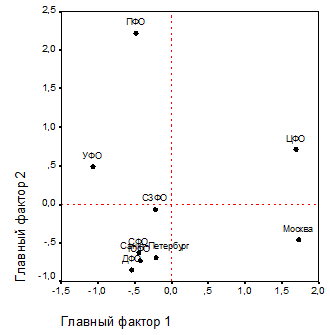
Рис. 8. Размещение территориальных образований РФ на плоскости главных факторов индексов затратных показателей
По диаграмме рис. 8 видно, что выделенные нами ранее четыре типа территориальных образований РФ проявляют себя и по значениям индексов главных факторов затратных показателей.
Выполненный комплекс исследований показал эффективность использования территориальных индексов в решении задач, связанных с временными сравнениями. В методическом плане представляет также интерес использованный в данном исследовании способ свертки временных рядов путем расчета МНК-оценок линейных моделей, аппроксимирующих тренды временных рядов. Такой подход позволяет дать более обоснованные оценки средних характеристик временных рядов, принятых в теории статистики – в данном случае, среднего уровня территориальных индексов и их среднегодовых приростов.
Читайте также
Библиографический список
- Карпухин А.А. Анализ территориального распределения затратных показателей российской инновационной системы // Наука и бизнес: пути развития, №6/2011.
- Регионы России. Социально-экономические показатели. 2010. Стат. сб. / Росстат. М., 2010.
- SPSS Base 8.0 для Windows. Руководство по применению. Перевод–Copyright 1998 СПСС Русь.
- Олдендерфер М.С., Блэшфилд Р.К. Кластерный анализ // Факторный, дискриминантный и кластерный анализ. М.: Финансы и статистика, 1989.
- Шуметов В.Г. Кластерный анализ в региональном управлении: учебное пособие. Орел: ОРАГС, 2001.
- Многомерный статистический анализ в экономике: Учеб. пособие для вузов / Л.А. Сошникова, В.Н. Тамашевич, Г. Уебе, М. Шефер. М.: ЮНИТИ-ДАНА, 1999.
- Колемаев В.А., Староверов О.В., Турундаевский В.Б. Теория вероятностей и математическая статистика: Учеб. пособие для экон. спец. вузов; Под ред. В.А. Колемаева. М.: Высш. шк., 1991.






