Прогнозирование доходов и расходов предприятия на основе мультипликативной модели временных рядов
Forecasting enterprise’s incomes and expenditures based on multiplicative model of dynamic series

Авторы
Аннотация
В данной практической статье авторами рассмотрено применение мультипликативной модели временных рядов с целью прогнозирования доходов и расходов предприятия.
Ключевые слова
доходы и расходы, анализ временных рядов, мультипликативная модель.
Рекомендуемая ссылка
Алеткин Павел Александрович, Кожемякова Виктория Викторовна, Шайдуллина Лилия Ильсуровна. Прогнозирование доходов и расходов предприятия на основе мультипликативной модели временных рядов // Современные технологии управления. ISSN 2226-9339. — №8 (20). Номер статьи: 2001. Дата публикации: 08.08.2012. Режим доступа: https://sovman.ru/article/2001/
Authors
Abstract
In this practical article authors consider the use of multiplicative model of dynamic series to forecast enterprise’s incomes and expenditures.
Keywords
incomes and expenditures, dynamic series analysis, multiplicative model.
Suggested citation
Aletkin Pavel Alexandrovich, Kozhemyakova Viktoriya Viktorovna, Shaydullina Liliya Ilsurovna. Forecasting enterprise’s incomes and expenditures based on multiplicative model of dynamic series // Modern Management Technology. ISSN 2226-9339. — №8 (20). Art. # 2001. Date issued: 08.08.2012. Available at: https://sovman.ru/article/2001/
В условиях нестабильности отечественной экономики по-прежнему остаются актуальными вопросы прогнозирования доходов и расходов промышленных предприятий. Качественно составленные прогнозы являются неотъемлимой частью процесса бюджетирования на предприятии.
В данной статье мы покажем, как спрогнозировать доходы и расходы предприятия на основе построения мультипликативной модели временных рядов. Временной ряд – это совокупность значений какого – либо показателя за несколько последовательных моментов или периодов времени [1].
Анализ временных рядов основан на сравнении каждой статьи отчетности за определенный период времени и определения тренда. Определение тренда означает определение основной тенденции динамики показателя без учета случайных влияний и индивидуальных особенностей отдельных периодов. Назначение анализа – это формирование возможных значений показателей в будущем.
Для прогнозирования объема продаж на краткосрочную перспективу на основе динамики временного ряда можно воспользоваться следующей моделью:
Y(t) = T(t) * S(t) * E(t), (1)
где: T(t) – временной тренд динамического ряда — регулярная компонента, характеризует общую тенденцию развития (глобальные изменения в экономике);
S(t) – сезонная компонента – характеризуется длительностью периода сезонных колебаний, их амплитудой, расположения максимума и минимума во времени. В зависимости от стабильности указанных характеристик во времени сезонная компонента носит постоянный или переменный характер;
E(t) – остаточная вариация (случайная составляющая), которая подразделяется на аномальную вариацию – неестественно большое отклонение временного ряда в результате чрезвычайной ситуации, который оказывает воздействие на единичное наблюдение; и на случайную вариацию – малые отклонения, которые невозможно предвидеть, в долгосрочной перспективе они могут как снизить, так и увеличить объем продаж.
Построение модели сводится к расчету значений Т, S или Е для каждого уровня ряда. Процесс построения модели включает в себя следующие шаги:
- выравнивание исходного ряда методом скользящей средней;
- расчет значений сезонной компоненты S;
- устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных в модели;
- аналитическое выравнивание уровней ряда и расчет значений Т с использованием полученного уравнения тренда;
- расчет полученных по модели значений;
- расчет абсолютных и относительных ошибок.
С целью прогнозирования доходов и расходов в работе использованы поквартальные данные о выручке ООО «Бирленд» за последние 4 года, представленные в таблице 1.
Таблица 1 — Исходные данные для анализа временных рядов объема продаж ООО «Бирленд»
| Период |
Объем продаж, тыс. руб. |
|||
|
2008 |
2009 |
2010 |
2011 |
|
|
1 квартал |
41508 |
66638 |
83721 |
85507 |
|
2 квартал |
69180 |
94404 |
115478 |
120244 |
|
3 квартал |
83016 |
111064 |
132799 |
133604 |
|
4 квартал |
71947 |
86075 |
101043 |
96195 |
|
Итого |
265651 |
358181 |
433041 |
435549 |
Построим график временного ряда доходов ООО «Бирленд» (рис. 1).
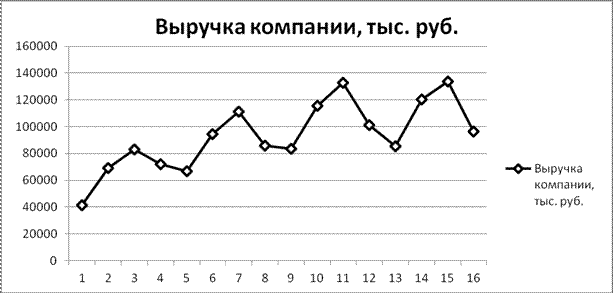
Рис 1. График временного ряда доходов ООО «Бирленд»
График временного ряда свидетельствует о наличии сезонных колебаний периодичностью 4 квартала. Выручка компании в весенне-летний период выше, чем в осенне-зимний период. Так как амплитуда сезонных колебаний возрастает, можно предположить существование мультипликативной модели. Определим ее компоненты.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней.
Результаты расчетов оценок сезонной компоненты представлены в таблице 2.
Таблица 2 — Расчет оценок средней сезонной компоненты
| № квартала | Выручка компании, тыс. руб. | Итого за четыре квартала | Скользящая средняя за четыре квартала | Центрированная скользящая средняя | Оценка сезонной компоненты |
|
1 |
41508 |
||||
|
2 |
69180 |
||||
|
3 |
83016 |
265651 |
66413 |
69554 |
1,194 |
|
4 |
71947 |
290781 |
72695 |
75848 |
0,949 |
|
5 |
66638 |
316006 |
79001 |
82507 |
0,808 |
|
6 |
94404 |
344054 |
86013 |
87779 |
1,075 |
|
7 |
111064 |
358181 |
89545 |
91681 |
1,211 |
|
8 |
86075 |
375264 |
93816 |
96450 |
0,892 |
|
9 |
83721 |
396337 |
99084 |
101801 |
0,822 |
|
10 |
115478 |
418073 |
104518 |
106389 |
1,085 |
|
11 |
132799 |
433041 |
108260 |
108483 |
1,224 |
|
12 |
101043 |
434826 |
108707 |
109302 |
0,924 |
|
13 |
85507 |
439592 |
109898 |
109999 |
0,777 |
|
14 |
120244 |
440397 |
110099 |
109493 |
1,098 |
|
15 |
133604 |
435549 |
108887 |
||
|
16 |
96195 |
Поскольку циклические колебания имеют периодичность в 4 квартала, просуммируем уровни ряда последовательно за каждые 4 квартала со сдвигом на один момент времени и определим условные годовые объёмы производства (колонка 3).
Разделив полученные суммы на 4, найдем скользящие средние (колонка 4). Полученные таким образом выровненные значения уже не содержат сезонной компоненты.
Поскольку скользящие средние получены осреднением четырех соседних уровней ряда, т.е. четного числа значений, они соответствуют серединам подынтервалов, состоящих из четверок чисел, т.е. должны располагаться между третьим и четвертым значениями четверок исходного ряда. Для того, чтобы скользящие средние располагались на одних временных отметках с исходным рядом, пары соседних скользящих средних ещё раз усредняются и получаются центрированные скользящие средние (колонка 5). При этом теряются первые две и последние две отметки временного ряда, что связано с осреднением по четырем точкам.
Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (колонка 6).
Шаг 2. Используем полученные оценки сезонной компоненты для расчета значений сезонной компоненты S. Для этого найдем средние за каждый квартал оценки сезонной компоненты Si. Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по всем кварталам должна равняться числу периодов в цикле. В нашем случае число периодов одного цикла (год) равно четырем кварталам. Результаты расчетов сведем в таблицу 3.
Таблица 3 — Расчет скорректированной сезонной компоненты
| Показатели | Год |
№ квартала, i |
|||
| I | II | III | IV | ||
|
1 |
— |
— |
1,194 |
0,949 |
|
|
2 |
0,808 |
1,075 |
1,211 |
0,892 |
|
|
3 |
0,822 |
1,085 |
1,224 |
0,924 |
|
|
4 |
0,777 |
1,098 |
— |
— |
|
| Итого за I-й квартал (за все годы) |
2,407 |
3,259 |
3,629 |
2,765 |
|
| Средняя оценка сезонной компоненты для I-го квартала, |
0,802 |
1,086 |
1,210 |
0,922 |
|
| Скорректированная сезонная компонента, |
0,798 |
1,081 |
1,204 |
0,917 |
|
По данным таблицы 3 видно, что сумма средних оценок сезонных компонент по всем четырем кварталам равна 4,02. Необходимо чтобы данная сумма равнялась четырем, для этого умножим каждое слагаемое на поправочный коэффициент, который рассчитывается следующим образом:
k = 4 / 4,02 = 0,9949.
Скорректированная сезонная компонента находится по формуле:
Si = ![]() i * k, i =
i * k, i = ![]() , (2)
, (2)
где: Si– скорректированная сезонная компонента;
![]() i– средняя оценка сезонной компоненты для i-го квартала;
i– средняя оценка сезонной компоненты для i-го квартала;
k–поправочный коэффициент.
Значения скорректированных сезонных компонент записаны в последней строке таблицы 3. Теперь их сумма равна четырем. Занесем значения в новую таблицу (колонка 3 таблицы 4).
Таблица 4 — Расчет временных рядов объема продаж ООО «Бирленд»
| T |
Yt |
Si |
|
Т |
T*S |
|
1 |
41508 |
0,798 |
51988 |
65528 |
52318 |
|
2 |
69180 |
1,081 |
64004 |
69181 |
74775 |
|
3 |
83016 |
1,204 |
68974 |
72834 |
87661 |
|
4 |
71947 |
0,917 |
78447 |
76486 |
70149 |
|
5 |
66638 |
0,798 |
83464 |
80139 |
63984 |
|
6 |
94404 |
1,081 |
87342 |
83792 |
90568 |
|
7 |
111064 |
1,204 |
92278 |
87445 |
105247 |
|
8 |
86075 |
0,917 |
93851 |
91098 |
83550 |
|
9 |
83721 |
0,798 |
104860 |
94751 |
75650 |
|
10 |
115478 |
1,081 |
106838 |
98404 |
106361 |
|
11 |
132799 |
1,204 |
110337 |
102056 |
122833 |
|
12 |
101043 |
0,917 |
110171 |
105709 |
96951 |
|
13 |
85507 |
0,798 |
107096 |
109362 |
87316 |
|
14 |
120244 |
1,081 |
111248 |
113015 |
122154 |
|
15 |
133604 |
1,204 |
111005 |
116668 |
140419 |
|
16 |
96195 |
0,917 |
104885 |
120321 |
110351 |
Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты, представим данное отношение в следующей формуле:
T * E = Y / S, (3)
Тем самым получим величины, которые содержат только тенденцию и случайную компоненту (колонка 4 в таблице 4).
Шаг 4. Определим трендовую компоненту в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни (Т + Е).
Линейный тренд найдем по следующей формуле:
Yt = a0 + ai *ti, (4)
где: Yt– выручка от продаж, тыс. руб.;
t – период по порядку;
ai – коэффициенты уравнения регрессии.
Далее воспользуемся средствами Excel для расчета коэффициентов регрессии.
Проследуем алгоритму: «Данные – Анализ данных – Регрессия». В появившемся окне в ячейке входной Y вводим диапазон данных колонки 4 таблицы 4, а в ячейке входной интервал Х – колонки 1 таблицы 4. Ставим флажок «Остатки», далее «ОК». На новом листе появляется «Вывод итогов». Необходимые нам значения коэффициентов уравнения регрессии определены как: а0 – это Y пересечение, а1 – переменная Х1, исходя из этого значение а0 будет равно 61875,04 и 3652,85– а1.
Уравнение тренда доходов ООО «Бирленд» имеет вид:
Т = 61875,04+ 3652,85 * t .
Подставляя в это уравнение значения t = 1,2,…,16, найдем уровни Т для каждого момента времени (колонка 5 таблицы 4).
Шаг 5. Найдем уровни ряда по мультипликативной модели, умножив уровни Т на значения сезонной компоненты для соответствующих кварталов (колонка 6 таблицы 4).
Прогнозирование по мультипликативной модели временного ряда сводится к расчету будущего значения временного ряда по уравнению модели без случайной составляющей в виде для мультипликативной модели.
![]() (5)
(5)
То есть прогнозные значения выручки от продаж на следующие 4 года по кварталам представлены в колонке 6 таблицы 4.
Из полученного прогноза видно, что товарооборот предприятия ООО «Бирленд» за 2012 — 2015 годы может составить 1490287 тыс. руб., зная сезонность сбыта можно спрогнозировать объем продаж в поквартальном разрезе. Так, объем продаж в первом квартале 2012 года составит 52318 тыс. руб., во втором – 74775 тыс. руб., в третьем – 87661 тыс. руб., в четвертом – 70149 тыс. руб.
Аналогичным образом спрогнозируем расходы предприятия по обычным видам деятельности. К расходам по обычным видам деятельности отнесем себестоимость продаж, управленческие и коммерческие расходы.
Поквартальные данные о расходах от обычных видов деятельности ООО «Бирленд» за последние 4 года представлены в таблице 5.
Таблица 5 — Исходные данные для анализа временных рядов расходов по обычным видам деятельности ООО «Бирленд»
| Период |
Расходы по обычным видам деятельности, тыс. руб. |
|||
|
2008 |
2009 |
2010 |
2011 |
|
|
1 квартал |
39721 |
63554 |
79384 |
82068 |
|
2 квартал |
66202 |
90035 |
111633 |
113198 |
|
3 квартал |
79443 |
105924 |
124037 |
130178 |
|
4 квартал |
68850 |
82091 |
89307 |
99048 |
|
Итого |
254217 |
341604 |
404360 |
424492 |
Построим график временного ряда расходов ООО «Бирленд» (рис. 2).
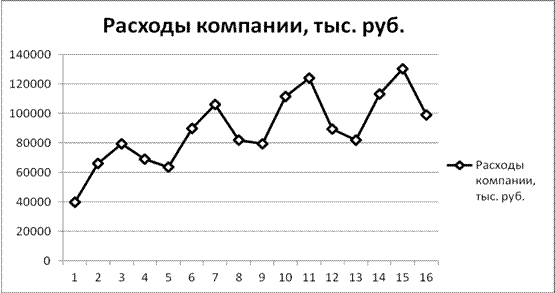
Рис. 2. График временного ряда расходов ООО «Бирленд»
График временного ряда свидетельствует о наличии сезонных колебаний периодичностью 4 квартала. Определим компоненты мультипликативной модели.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Методика, применяемая на этом шаге, полностью совпадает с методикой анализа временного ряда объема продаж организации. Результаты расчетов оценок сезонной компоненты представлены в таблице 6.
Таблица 6 — Расчет оценок средней сезонной компоненты
| № квартала |
Расходы компании, тыс. руб. |
Итого за четыре квартала |
Скользящая средняя за четыре квартала |
Центрированная скользящая средняя |
Оценка сезонной компоненты |
|
1 |
39721 |
||||
|
2 |
66202 |
||||
|
3 |
79443 |
254217 |
63554 |
66533 |
1,194 |
|
4 |
68850 |
278049 |
69512 |
72491 |
0,950 |
|
5 |
63554 |
301882 |
75471 |
78781 |
0,807 |
|
6 |
90035 |
328363 |
82091 |
83746 |
1,075 |
|
7 |
105924 |
341604 |
85401 |
87380 |
1,212 |
|
8 |
82091 |
357433 |
89358 |
92058 |
0,892 |
|
9 |
79384 |
379031 |
94758 |
97022 |
0,818 |
|
10 |
111633 |
397144 |
99286 |
100188 |
1,114 |
|
11 |
124037 |
404360 |
101090 |
101426 |
1,223 |
|
12 |
89307 |
407045 |
101761 |
101957 |
0,876 |
|
13 |
82068 |
408610 |
102152 |
102920 |
0,797 |
|
14 |
113198 |
414750 |
103688 |
104905 |
1,079 |
|
15 |
130178 |
424492 |
106123 |
||
|
16 |
99048 |
Шаг 2. Используем полученные оценки сезонной компоненты для расчета значений сезонной компоненты S. Результаты расчетов сведем в таблицу 7.
Таблица 7 — Расчет оценки сезонной компоненты
| Показатели | Год |
№ квартала, i |
|||
| I | II | III | IV | ||
|
1 |
— | — |
1,194 |
0,950 |
|
|
2 |
0,807 |
1,075 |
1,212 |
0,892 |
|
|
3 |
0,818 |
1,114 |
1,223 |
0,876 |
|
|
4 |
0,797 |
1,079 |
— | — | |
| Итого за I-й квартал (за все годы) |
2,422 |
3,268 |
3,629 |
2,717 |
|
| Средняя оценка сезонной компоненты для I-го квартала, |
0,807 |
1,089 |
1,210 |
0,906 |
|
| Скорректированная сезонная компонента, |
0,805 |
1,086 |
1,206 |
0,903 |
|
В данном случае поправочный коэффициент равен:
k = 4 / 4,012 = 0,9969.
Значения скорректированных сезонных компонент записаны в последней строке таблицы 7. Теперь их сумма равна четырем. Занесем значения в новую таблицу (колонка 3 таблицы 8).
Таблица 8 — Расчет временных рядов расходов по обычным видам деятельности ООО «Бирленд»
| T |
yt |
Si |
Т |
T*S |
|
|
1 |
39721 |
0,805 |
49347 |
61604 |
49587 |
|
2 |
66202 |
1,086 |
60955 |
65223 |
70838 |
|
3 |
79443 |
1,206 |
65874 |
68843 |
83023 |
|
4 |
68850 |
0,903 |
76246 |
72462 |
65433 |
|
5 |
63554 |
0,805 |
78955 |
76081 |
61241 |
|
6 |
90035 |
1,086 |
82899 |
79701 |
86562 |
|
7 |
105924 |
1,206 |
87832 |
83320 |
100482 |
|
8 |
82091 |
0,903 |
90909 |
86940 |
78506 |
|
9 |
79384 |
0,805 |
98621 |
90559 |
72894 |
|
10 |
111633 |
1,086 |
102785 |
94178 |
102285 |
|
11 |
124037 |
1,206 |
102852 |
97798 |
117942 |
|
12 |
89307 |
0,903 |
98900 |
101417 |
91580 |
|
13 |
82068 |
0,805 |
101956 |
105036 |
84548 |
|
14 |
113198 |
1,086 |
104226 |
108656 |
118009 |
|
15 |
130178 |
1,206 |
107944 |
112275 |
135401 |
|
16 |
99048 |
0,903 |
109688 |
115894 |
104653 |
Далее воспользуемся средствами Excel для расчета коэффициентов регрессии, по аналогии с анализом временного ряда объема продаж. Значение а0 будет равно 57984,66 и 3619,36 – а1.
Уравнение тренда расходов ООО «Бирленд» имеет вид:
Т = 57984,66 + 3619,36 * t .
Подставляя в это уравнение значения t = 1,2,…,16, найдем уровни Т для каждого момента времени (колонка 5 таблицы 8).
Прогнозные значения расходов по обычным видам деятельности на следующие 4 года по кварталам представлены в колонке 6 таблицы 8.
Из полученного прогноза видно, что расходы предприятия ООО «Бирленд» за 2012 и 2015 годы могут составить 830080,97 тыс. руб., зная сезонность сбыта можно спрогнозировать расходы по текущей деятельности в поквартальном разрезе. Так, расходы ООО «Бирленд» в первом квартале 2012 года составят 49587 тыс. руб., во втором – 70838 тыс. руб., в третьем – 83023 тыс. руб., в четвертом – 65433 тыс. руб.
Сопоставив прогнозные значения выручки от продаж и расходов по обычной деятельности, можно так же найти прогнозные значения прибыли от продаж в поквартальном разрезе. Расчеты приведены в таблице 9.
Таблица 9 — Прогноз прибыли от продаж ООО «Бирленд»
| Показатели |
Объем продаж |
Расходы по обычной деятельности |
Прибыль от продаж |
|
|
2012 год |
1 кв. |
52318 |
49587 |
2731 |
| 2 кв. |
74775 |
70838 |
3937 |
|
| 3 кв. |
87661 |
83023 |
4638 |
|
| 4 кв. |
70149 |
65433 |
4716 |
|
|
Итого за 2012 год |
284903 |
268882 |
16022 |
|
|
2013 год |
1 кв. |
63984 |
61241 |
2743 |
| 2 кв. |
90568 |
86562 |
4006 |
|
| 3 кв. |
105247 |
100482 |
4765 |
|
| 4 кв. |
83550 |
78506 |
5043 |
|
|
Итого за 2013 год |
343349 |
326791 |
16557 |
|
|
2014 год |
1 кв. |
75650 |
72894 |
2755 |
| 2 кв. |
106361 |
102285 |
4075 |
|
| 3 кв. |
122833 |
117942 |
4891 |
|
| 4 кв. |
96951 |
91580 |
5371 |
|
|
Итого за 2014 год |
401794 |
384701 |
17093 |
|
|
2015 год |
1 кв. |
87316 |
84548 |
2768 |
| 2 кв. |
122154 |
118009 |
4145 |
|
| 3 кв. |
140419 |
135401 |
5018 |
|
| 4 кв. |
110351 |
104653 |
5699 |
|
|
Итого за 2015 год |
460240 |
442611 |
17629 |
|
|
Итого |
1490287 |
1422985 |
67301 |
|
По данным таблицы видно, что прогнозная совокупная прибыль от продаж ООО «Бирленд» за 2012-2015 годы составит 67301 тыс. руб. Выручка от продаж больше в 2015 году, поэтому наибольшая прогнозная прибыль ожидается в 2015 году, она в данный период составит 17629 тыс. руб. Данный показатель растет с каждым годом, так в 2012 году прибыль от продаж составляет 16022 тыс. руб., в 2013 году – 16557 тыс. руб., в 2014 году – 17093 тыс. руб., в 2015 году – 17629 тыс. руб., что может свидетельствовать о расширении деятельности бизнеса, продажах более рентабельной продукции пользующейся спросом, эффективном менеджменте.
Полученные в результате прогнозирования данные о размере будущих доходов и расходов предприятия могут быть использованы для составления бюджета финансовых результатов, а также расчета показателей рентабельности деятельности на перспективу.
Читайте также
Библиографический список
- Костромин А.В. Эконометрика: Курс лекций. – Казань: Изд-во «Таглимат», 2004. – 136 с.
- Любушин Н.П. Комплексный экономический анализ хозяйственной деятельности / Н.П.Любушин. – 3-е изд. – М.: ЮНИТИ-ДАНА, 2006. – 448 с.
- Экономический анализ активов организации / под ред. Д.А.Ендовицкого. – М.: Эксмо, 2009. – 608 с.
References
- Kostromin A.V. Econometrics: course of lectures. – Kazan: Taglimat, 2004. – 136 p.
- Lyubushin N.P. Complex economical analysis of business activity / N.P.Lyubushin – 3rd edition. – M.: Yunity-Dana, 2006. – 448 p.
- Economical analysis of enterprise’s assets / under D.A.Endovizkiy. – M.: Eksmo, 2009. – 608 p.






