Моделирование процессов адаптивного управления бизнесом
Modeling of processes of an adaptive business management
Авторы
Аннотация
На основе анализа систем адаптивного правления бизнесом предложен оригинальный вариант реальной системы адаптивного управления, в основу которой использованы динамические рекурсивные модели денежных потоков прогнозных и реальных данных. Предложены определения и проведено моделирование шкал и интервалов модельного времени в системе управления, а также порогов наблюдений и условий изменения (коррекции) управленческих решений. Процесс адаптивного управления проиллюстрирован на основе предложенного автором сценария развития бизнеса.
Ключевые слова
адаптивное управление, адаптивная модель, прогнозная модель, обратная связь, регулятор, шкала модельного времени, интервалы наблюдений, сценарий моделирования.
Рекомендуемая ссылка
Карев Владимир Петрович, Карев Дмитрий Владимирович. Моделирование процессов адаптивного управления бизнесом // Современные технологии управления. ISSN 2226-9339. — №4 (4). Номер статьи: 0403. Дата публикации: 08.04.2011. Режим доступа: https://sovman.ru/article/0403/
Authors
Abstract
On the basis of the analysis of systems of adaptive management board business proposed the original version of the real system of adaptive management, the basis of which used dynamic recursive model cash flow forecast and real data. Proposed definitions and the simulation of scales and intervals of model time in the control system, as well as the thresholds observations and conditions of changing (correction) of the administrative decisions. The process of adaptive management is illustrated on the basis proposed by the author of the script of development of business.
Keywords
adaptive control, adaptive model, the forecast model, feedback, regulator, the scale of the model time intervals observations, scenario modeling.
Suggested citation
Karev Vladimir Petrovich, Karev Dmitry Vladimirovich. Modeling of processes of an adaptive business management // Modern Management Technology. ISSN 2226-9339. — №4 (4). Art. # 0403. Date issued: 08.04.2011. Available at: https://sovman.ru/article/0403/
Управлять трудно, поэтому умные с охотой препоручают эту обязанность дуракам — для них трудностей не существует!
Введение
Общеизвестно, что управление объектами, различными по своей природе — техническими, социально-экономическими, военными системами и т.п., можно сформулировать в виде трёх общих принципов, включающих в себя:
- единство структурно-функциональных описаний управляемой системы;
- наличие внешней среды, определяющей поведение и функционирование управляемой системы;
- цели, реализуемые в виде функций или задач оптимального управления, а также критерии оптимальности.
Вместе с тем существенное отличие экономических систем, в частности предприятий, создаваемых с целью бизнеса, от технических обусловлено качественным различием их параметров. Параметры в технических системах имеют, как правило, строго определенные физические размерности и закономерности поведения. Их формализация происходит на основе определенных физических законов и с применением сложных, но в целом строгих математических описаний. Для экономических систем проведение математической формализации трудно реализуемо вследствие возникающих трудностей описания поведения их элементов и взаимосвязей между этими элементами за счёт неопределенности изменения внутренних параметров, в том числе — за счёт человеческого фактора. Но всё же главной причиной трудностей формализации параметров и собственно процесса управления является высокая степень неопределенности параметров внешней среды — рынка, конкуренции, возможных периодических кризисов и иных видов рисков.
Одним из возможных способов компенсации трудностей формализации параметров экономических систем является применение методов адаптивного управления подобными системами. Под «адаптивным управлением»понимается совокупность методов управления, позволяющих синтезировать системы управления, имеющих возможность изменять её параметры регулятора или структуру регулятора в зависимости от изменения параметров объекта управления или внешних возмущений, действующих на объект управления. «Регулятор» — в теории управления устройство, которое следит за работой объекта управления как системы и вырабатывает для неё управляющие сигналы [1].
В данной работе на основе анализа различных принципов адаптивного управления предложен вариант системы адаптивного управления, реализованной на основе параллельно работающих динамических моделей внешних и внутренних денежных потоков объекта управления. Проведен анализ временных характеристик процесса управления, а также рассмотрен один из возможных сценариев управления предприятием и процесса принятия управленческих решений.
1. Обзор известных методов адаптивного управления предприятием
На Рис. 1 представлена обобщенная авторами структурно — функциональная модель адаптивного управления, описываемая в частности в работах [2, 3] и других. При адаптивном управлении структура регулятора позволяет производить анализ результатов моделирования на прогнозной модели и совершать итерационные вычисления по поиску оптимального значения параметров матрицы рассогласования.
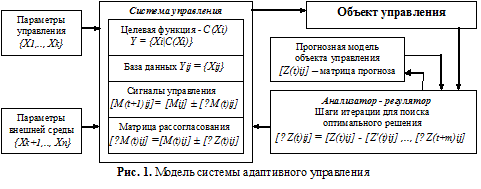
Для целевой функции С, включающей в себя совокупность всех параметров внешней среды и параметров управления Xi, множество внутренних параметров управляемого объекта и системы управления — Y можно выразить как:
![]() (1)
(1)
Рассмотрим нюансы вариантов реализации систем адаптивного управления.
В терминах ДОТУ — «достаточно общей теории управления», заимствованных из вычислительной техники, используется понятие «управление по схеме предиктор-корректор». Оно строится на основе прогнозирования в процессе управления поведения замкнутой системы (объект плюс система управления) на основе информации о её текущем и прошлых состояниях и воздействии на неё окружающей среды. Прогнозная информация подаётся на вход анализатора-регулятора, а система управления реагирует не только на уже свершившиеся отклонения замкнутой системы от идеального режима, но и на те, которые спрогнозированы к осуществлению. Таким образом, в схеме предиктор—корректор обратная связь замыкается через прогнозируемое будущее [4].
В работе [5] предлагается обеспечивать обучение адаптивных систем управления на основе метода прецедентов. Прецедент (от лат. praecedens — предшествующий) — случай или событие, имевшие место в прошлом и служащие примером или основанием для аналогичных действий в настоящем. Вывод на основе прецедентов — это метод принятия решений, в котором используются знания о предыдущих ситуациях или случаях (прецедентах). В базе данных ищется похожий прецедент в качестве аналога с возможной адаптацией к текущему случаю, либо производится поиск нового решения, которое вносится в базу прецедентов вместе со своим решением для его возможного последующего использования. Более формальное определение дано в работе [6].
Наиболее интересна двушкальная система адаптивного управления экономическими системами, представленная в работе [7]. Она состоит из элементов «быстрой рабочей шкалы времени» — моделей непрерывно рассчитываемых альтернативных вариантов бизнес-планов, динамического анализа рисков, принятия решений по выбору вариантов управления, настраиваемой имитационной модели управляющих воздействий и собственно управляющих органов. Элемент «медленной шкалы времени» — управляемый объект, реализующий свой бизнес (производство товаров и услуг) в реальном масштабе времени.
Понятия быстроты или медленности двух шкал в достаточной степени условны. Любое ритмично работающее производство имеет свой суточный, недельный, месячный и более длительные планы, которые теоретически ограничены сверху его производственной мощностью, а снизу — возможностями рынка сбыта потреблять производимые и продаваемые на этом рынке его товары или услуги. Но если система управления предприятия технически обеспечивает возможности генерировать в сутки достаточное для принятия управляющих решений количество вариантов управления, то это процесс неизмеримо более быстрый, чем возможность изменения параметров реализуемого производственного плана.
Если проблемы быстродействия моделирования вариантов управления и принятия решений по ним решены, то главными становятся проблемы качества этих вариантов, во-первых, — точности прогнозирования на основе выбранных критериев оценки, во-вторых, — формирования шкал модельного времени наблюдений, индикации моментов изменения положения управляемой системы относительно внешней среды и принятия решений на проведение управляющих воздействий.
2. Динамическая схема адаптивного управления
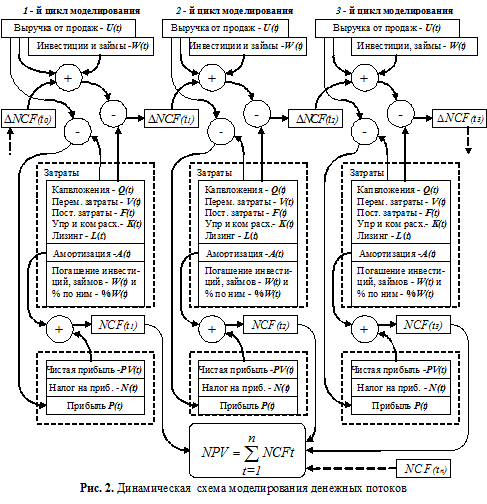
В работе авторов [8] предложена оригинальная динамическая схема моделирования денежных потоков (Cash Flow) в бизнес-планах: чистого денежного потока по периодам планирования — NCFt, суммарного чистого денежного потока по всем периодам — NPV и чистого дисконтированного денежного потока — NPVd.
В настоящее время используются традиционные схемы статического моделирования денежных потоков, когда при расчете параметров денежных потоков в заданном периоде параметры моделирования не меняются. Связь осуществляется на этапе суммировании по всем периодам NCFt и вычислении либо NPV, либо дальнейшего значения NPVd. Моделирование заключается в последовательном переборе входных данных и получении наборов результатов. Если результат моделирования приемлем, то моделирование считается законченным, если нет — перебор продолжают.
Предлагаемая динамическая схема моделирования представлена на Рис. 2. Значение остатка оборотных средств в t — м периоде планирования описывается следующим беллмановским рекуррентным выражением:
![]() (2)
(2)
ΔNCF(t-1) — остаток денежных средств в (t — 1) — м периоде планирования.
S(t)— поступления предприятия, включая:
U(t) выручку от продаж продукции, финансовые заимствования (инвестиции и кредиты), внереализационные доходы в t — м периоде планирования;
Z(t) — затраты предприятия в t — м периоде планирования.
При планировании и расчете денежных потоков выполняются следующие аксиоматические условия.
В Таблице 1 представлен пример оформления бизнес-плана, смоделированного на основе схемы, представленной на Рис. 2. и условий (2) и (3) Полное описание математических моделей предлагаемой схемы и примеры моделирования приведены в работе одного из авторов [9].
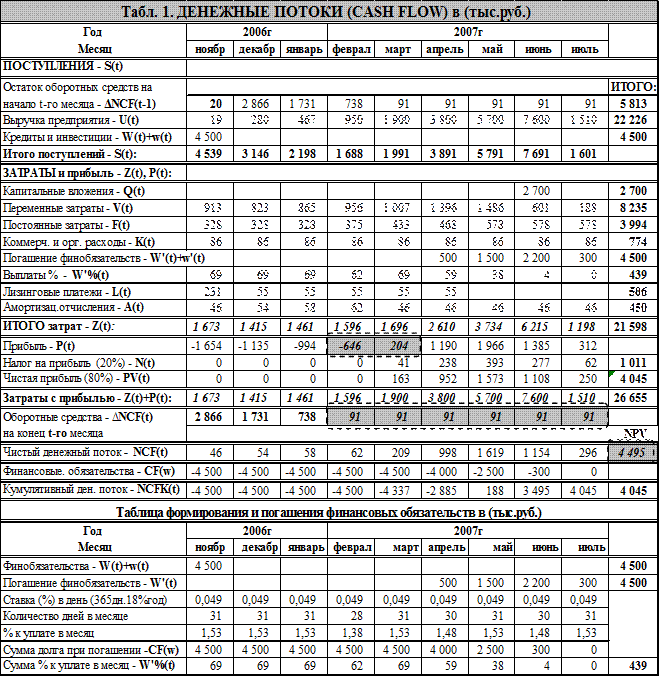
Принципиальным достоинством предлагаемой модели является её инвариантность к моделированию денежных потоков для собственного или инвестиционного капитала. Следует правильно задать данные, например, для модели денежного потока собственного капитала нет необходимости задавать параметры внешних финансовых обязательств — кредитов или инвестиций, а для модели денежного потока инвестированного капитала эти параметры задаются в пределах поставленных задач – оценки, инвестиционного проектирования или управления бизнесом.
Из условия (3) выведен аксиоматический принцип чувствительности: «Сколь угодно малое изменение в периоде моделирования численного значения любого входного параметра моделируемой системы приводит к пропорциональным изменениям численных значений всех выходных моделируемых параметров на этом и всех последующих после этого периодах».
Приведенный пример моделирования демонстрирует возможности динамической модели, как программируемого автомата, практически недостижимые для традиционной схемы моделирования денежных потоков.
И, наконец, главное. Встраиваемые в двушкальную модель управления подобные динамические модели управления позволяют без труда строить в реальном масштабе времени любое количество копий сравниваемых между собой моделей состояний прогнозных и реальных объектов управления и формировать сигналы рассогласования. Поэтому она была использована в качестве базового элемента для разработки структуры оригинальной системы адаптивного управления — Рис. 3.
Рис. 3. Структура системы адаптивного управления предприятием
Процесс управления осуществляется следующим образом. Задано множество А параметров {X1, X2… Xn} модели Cash—Flowпрогнозных планов и множество В попарно однородных с А параметров — {Y1, Y2… Yn} в модели Cash—Flowпараметров наблюдения реального процесса бизнеса. При этом для подмножеств попарно однородных, но разновеликих параметров, — А1{X1, X2… Xm} и В1{Y1, Y2… Ym} выполняются условия:
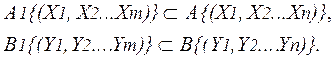 (4)
(4)
Условие (4) позволяет осуществить следующую операцию поэлементного вычитания параметров из подмножества А1подмножества В1:
![]() (5)
(5)
![]() — подмножество рассогласований параметров.
— подмножество рассогласований параметров.
В модели анализа рассогласований информация, содержащаяся в подмножествах А1, В1 иC1, в совокупности с информацией о рисках бизнеса используется лицом, принимающим решение (ЛПР) для принятия решения об использовании того или иного варианта управления.
3. Определение шкал модельного времени
Назовём «шкалой модельного времени» — множество интервалов времени ![]() , на которых наблюдается изменение дискретных значений параметров моделируемого или управляемого предприятия.
, на которых наблюдается изменение дискретных значений параметров моделируемого или управляемого предприятия.
Введем понятие «порога наблюдений»барьерной величины m— го параметра рассогласования — ∆Zm в модельном времени, для регистрации значения возможной точки бифуркации, когда при превышении порога ∆Zmiв j-й период времени потенциально возможна, но ещё не обязательна смена состояния управляемой системы. Минимальное рассогласование — ∆Zmj связанно с Zmследующей зависимостью:
![]() (6)
(6)
Величина интервала времени — ∆tnb, в течение которого формируется рассогласование ∆Zmj, называется «минимальным интервалом наблюдений». Последовательность ∆tnb, просуммированных по величине длительности интервала, называется «модельным временем наблюдений» и обозначается как — Tnb. На Рис. 4 представлен процесс формирования параметра рассогласования ∆Zm.
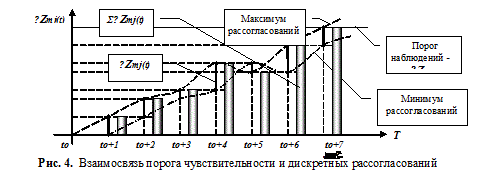
Расчёт величины порога чувствительности — ∆Zmi в зависимости от величин рассогласования — ∆Zmj осуществляется на основании следующего выражения:
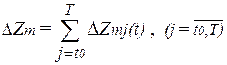 (7)
(7)
Наблюдение и анализ интервала времени Tnb формирования ∆Zmпозволили сформировать новый ряд модельного времени — «модельное время индикации моментов потенциальной бифуркации» с интервалом индикации точек бифуркации — Tbf длительностью примерно в неделюитретье модельное время — «время принятия и реализации решений» с интервалом — Trhпримерно в один календарный месяц.
4. Анализ порогов, точек бифуркации и моментов принятия решений
Анализ основных параметров денежных потоков, используемых при управлении, осуществляется из ряда параметров, сформированных в работе [8] при анализе модели Cash—Flowпрогнозных планов модели Cash—Flowпараметров наблюдения реального процесса бизнеса. К вспомогательным параметрам, используемым для формирования планов выручки и затрат, или наблюдения за потоком фактических данных в t — м периоде планирования/наблюдения, относятся:
- K(t) — себестоимость единицы продукции;
- P(t) — отпускная цена единицы продукции;
- X(t) — количество единиц продукции, продаваемых в t — м периоде планирования/наблюдения;
К выходным параметрам, определяющим базовые финансовые показатели предприятия в t — м периоде планирования/наблюдения, относятся:
- S(t) — затраты предприятия, направляемые на обеспечение его хозяйственной деятельности и погашение финансовых обязательств.
- U(t) — выручка от реализации товаров и услуг;
- NCF(t) — значение чистого денежного потока (чистая прибыль плюс амортизация);
- ∆NCF(t) — остаток оборотных средств.
В общем случае под «периодом планирования/наблюдения» понимается интервал производства и продаж, равный интервалу принятия решения — Trhв один календарный месяц и более — квартал/год. В реальной системе управления эти данные отслеживаются ежесуточно, т.е. в каждом интервале наблюдения.
В предыдущем подразделе мы ввели понятие «порога наблюдений» и принципов его формирования на основе его дискретных составляющих. Но ввести понятие и определить способ его формирования — полдела. Необходимо для каждого из существенных вспомогательных или выходных параметров в процессе производства и продаж определить процедуру численного вычисления значений этого «порога чувствительности», которые являются критическими для процесса производства и продаж и потенциально требуют возможного принятия решений о коррекции параметров управления.
Если предприятие работает долго, накапливаются ретроспективные данные о его производственно-финансовой деятельности, жизненных циклах предприятия и производимых им изделий. При этом несложно построить тренд ретроспективных данных и далее провести экстраполяцию прогнозных данных.
С другой стороны данные о величине порога чувствительности, формируемые за неделю, естественно, не могут дать достоверного суждения о текущем поведении бизнеса. Вот если накопленная за эту неделю наблюдений величина порога составляет единицы процентов роста или спада продаж от планируемого месячного выпуска — это, безусловно, серьезно, особенно, если данные экстраполяции накопленных за периоды наблюдения данных свидетельствуют о сохранении или, тем более, — усилении выявленной тенденции.
На Рис. 5 графически представлены изменения трёх параметров управления — X(t), U(t) иS‘(t) — стоимости материальных запасов в затратах S(t) — на всех трёх интервалах модельного времени. События, проиллюстрированные на рисунке, развиваются по следующему, вполне правдоподобному сценарию.
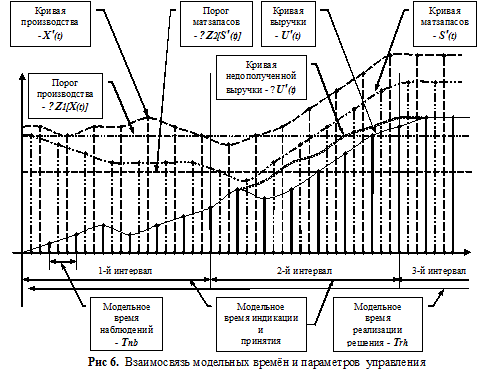
- На первом интервале модельного времени индикации выявлена тенденция роста выручки — U’(t) от продаж продукции предприятия. Рост достаточно значительный на 14,8% за интервал индикации — 7 дней.
- Принимается решение — увеличить объёмы производства в единицах продукции — X(t) с целью удовлетворения внезапно выросшего спроса на продукцию предприятия.
- Одновременно к концу первого интервала индикации отмечено снижение объёмов производства в единицах продукции — X‘(t) по внутрипроизводственным причинам (станок сломался — ремонтировали, специалисты уволились — новых нанимали и т.п.). Данный факт отражен на падении объёмов производства ниже расчётного минимального порога производства в начале второго интервала модельного времени — ∆Z1[X(t)].
- Рост объёмов продаж потребовал повышенного расхода материальных запасов S‘(t): сырья, материалов или полуфабрикатов. На первом интервале модельного времени индикации принимается решение о закупке и допоставке дополнительных материальных запасов.
- В начале второго интервала модельного времени индикации принятое на первом интервале решение начинает выполняться: оплачена и организована поставка дополнительных материальных запасов, наняты дополнительные рабочие или организовано продление рабочих смен за счёт сверхурочной работы основного персонала.
- Однако недостаток материальных ресурсов, упавших в начале второго интервала модельного времени ниже расчётного минимального порога материальных запасов — ∆Z2[S(t)], не позволяет обеспечить не только рост, но и подержание достигнутого объёма выручки от продаж. Абсолютная величина ежедневной выручки — U’(t) падает. Величина потенциально возможной, но недополученной выручки растёт. Кривая недополученной выручки также приведена на Рис. 5.
- Лишь к середине второго интервала модельного времени индикации поставка на склад дополнительных материальных запасов, и достаток рабочего персонала позволяют организовать ритмичный и последовательный рост выпуска и продаж продукции. Абсолютная величина ежедневной выручки — U’(t) начала расти, а величина потенциально возможной, но недополученной выручки начала падать.
- В начале третьего интервала модельного времени индикации спрос на продукцию и, соответственно, абсолютная величина ежедневной выручки от продаж — U’(t) растёт, а затем стабилизируется. Поставки материальных запасов и производство в единицах продукции также стабилизируется.
Какие же выводы можно сделать из результатов представленного сценария адаптивного управления?
1. Основной причиной недополучения выручки являются ошибочно установленные при прогнозном планировании модели Cash—Flowпрогнозных планов — (∆X(t), ∆S(t), ∆U(t)) пороги минимальных материальных запасов и единиц выпускаемой продукции, а также задержки их сверхнормативных поставок и задержки организации дополнительного производства продукции не позволили получить дополнительную сверхнормативную выручку.
2. Проведенные менеджментом предприятия мероприятия по исправлению критической ситуации в реальном масштабе времени происходили с запаздыванием и не позволили полностью реализовать производственно-сбытовой потенциал предприятия.
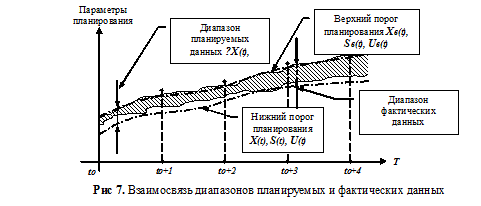
3. Для своевременного реагирования на описанные в сценарии критические ситуации необходимо поддерживать уровни материальных запасов и единиц продукции на некотором избыточном уровне. Иными словами, результаты прогнозного планирования должны представляться в виде некоторого диапазона, в который должны укладываться формируемые далее фактические данные деятельности предприятия. Рис. 7 иллюстрирует, как возможный диапазон изменения фактических данных модели Cash—Flowпараметров наблюдения из приведенного выше сценария — ∆X‘(t), ∆S‘(t), ∆U'(t)связан с диапазоном аналогичных величин произведенного заранее на модели Cash—Flowпрогнозных планов — {∆X (t), ∆S(t), ∆U(t)}.
4. Приведенное на Рис. 7 соотношение диапазонов прогнозного планирования и фактических на этот период планирования данных иллюстрирует ситуацию практически оптимального управления в данной адаптивной системе.
Заключение.
Ввиду необъятности данной темы авторы изложили фрагментарно лишь некоторые свои взгляды на процессы моделирования и управления адаптивных систем. В том числе:
- В данной работе проведен анализ вариантов организации систем адаптивного управления и предложен оригинальный вариант реальной системы адаптивного управления предприятием, в основу которой использованы динамические рекурсивные модели денежных потоков прогнозных и реальных данных.
- Предложены определения и проведено моделирование шкал и интервалов модельного времени в системе управления, а также порогов наблюдений и условий изменения (коррекции) управленческих решений.
- В качестве основного элемента системы управления предложена модель анализа рассогласований, момента бифуркации и принятия решений, в которой ключевым элементом является ЛПР. Сам процесс адаптивного управления проиллюстрирован предложенным авторами вполне правдоподобным сценарием.
- Безусловно, первичным и самым важным элементом адаптивного управления является прогнозный анализ и сценарное планирование возможных ситуаций деятельности управляемого объекта и синтез прогнозной модели управления. Подобные задачи прогнозирования, типичны не только для проектирования систем управления, но и для инвестиционного проектирования и оценки бизнеса.
- Для поддержания процесса оперативного и эффективного управления менеджменту предприятия необходима информационная и аппаратная среда в виде ERP-системы, настроенной на создание и реализацию в реальном времени прогнозной модели и модели оперативного управления ресурсами бизнеса предприятия.
- Процесс прогнозного анализа и сценарного планирования вполне реализуем посредством применения численных аналитических и статистических математических методов, но сложен и кропотлив. Если у кого-то возникают по этому поводу сомнения, советуем ещё раз прочитать эпиграф к данной работе.
Читайте также
Библиографический список
- Математика и кибернетика в экономике. Экономика. М.: 1975.
- Срагович В.Г. Адаптивное управление. — М.: Наука, 1981.
- Скурихин В.И., Забродский В.А., Копейченко Ю.В. Проектирование систем адаптивного управления производством. Х.: «Вища школа», 1984.
- Достаточно общая теория управления: Учебный курс факультета прикладной математики — процессов управления СПГУ (1997 — 2003 гг.), http://www. erlib.com.
- Карпов Л. Е., Юдин В. Н. Адаптивное управление по прецедентам, основанное на классификации состояний управляемых объектов. Труды Института системного программирования РАН. 1996.
- BundyAlan, editor. Artificial Intelligence Techniques. Springer Verlag. 1997.
- В.С. Анфилатов, А.А. Емельянов, А.А. Кукушкин. Системный анализ в управлении: Учебн. пособие под редакцией А.А. Емельянова. М.: Финансы и статистика, 2002.
- Карев В.П. Карев Д.В. Применение имитационного моделирования для расчета дисконтированных денежных потоков при оценке бизнеса // Вопросы оценки. Профессиональный научно-практический журнал. 2004. №3.
- Карев В.П. Математическое моделирование бизнеса — оценка, инвестиционное проектирование, управление предприятием. М.: Маросейка. 2010.
References
- Mathematician and cybernetics in economy. Economy. М: 1975.
- Sragovich of Century Adaptive management. – М: the Science, 1981.
- Skurihin V. I, Zabrodsky Century А, Kopejchenko JU.V.designing of systems of adaptive production management. Х: «Vishcha school», 1984.
- Enough general theory of management: the Training course of faculty of applied mathematics – managerial processes СПГУ (1997 – 2003), http:// www. erlib.com.
- Carps of L. Е, Yudin V. N. Adaptive management on the precedents, based on classification of conditions operated obek eat. Works of Institute of system programming of the Russian Academy of Sciences. 1996.
- Bundy Alan, editor. Artificial Intelligence Techniques. Springer Verlag. 1997.
- V.S.Anfilatov, A.A.Yemelyan, A.A.cuckoo. The system analysis in management. The grant under A.A.Yemelyanov’s edition. М: the Finance and statistics, 2002.
- Karev V.P., Karev D.V.application of imitating modeling for calculation of the discounted monetary streams at a business estimation//estimation Questions. Professional scientifically-practical magazine. 2004. №3.
- Karev V.P. Mathematical modeling of business – an estimation, inve-stitsionnoe designing, operation of business. М: Maroseyka. 2010.




