Методика формирования обобщенного индикатора воспроизводства кадрового научного потенциала российской инновационной системы
Method of forming of the generalized indicator of the reproduction of the human scientific potential of the russian innovation system

Авторы
Аннотация
Данная публикация носит методический характер и содержит описание этапов статистических исследований, конечная цель которых – разработка обобщенного индикатора воспроизводства кадрового научно-инновационного потенциала экономических подсистем РФ. Эмпирической базой исследований являлись временные ряды показателей воспроизводства научных кадров в федеральных округах и крупных научных центров в 2000-2009 гг.
Ключевые слова
инновационная деятельность, кадровый потенциал, аспирантура, докторантура.
Рекомендуемая ссылка
Котельников Сергей Александрович. Методика формирования обобщенного индикатора воспроизводства кадрового научного потенциала российской инновационной системы // Современные технологии управления. ISSN 2226-9339. — №10 (22). Номер статьи: 2203. Дата публикации: 08.10.2012. Режим доступа: https://sovman.ru/article/2203/
Authors
Abstract
This publication is of a methodical nature and contains a description of the stages of statistical research, which ultimate goal - the development of a generalized indicator of the reproduction of the human resources of the scientific and innovation potential of the economic subsystems of the Russian Federation. The empirical base of the research were the time series of indicators of the reproduction of the scientific personnel in the Federal districts and major research centers in 2000-2009.
Keywords
innovation, human resources, postgraduate, doctoral.
Suggested citation
Kotel'nikov Sergej Aleksandrovich. Method of forming of the generalized indicator of the reproduction of the human scientific potential of the russian innovation system // Modern Management Technology. ISSN 2226-9339. — №10 (22). Art. # 2203. Date issued: 08.10.2012. Available at: https://sovman.ru/article/2203/
В нашей предыдущей публикации [1] рассматривались вопросы распределения и динамики изменения показателей воспроизводства кадрового научно-инновационного потенциала российской инновационной системы. Были получены оценки средних по РФ показателей, выявлены их изменения в период 2000-2009 гг. В частности, показано, что число организаций, ведущих подготовку аспирантов и докторантов, за этот период заметно увеличилось, увеличилась и численность аспирантов, тогда как численность докторантов практически не изменилась. Выявлено также, что «мощность» аспирантур, как основного звена в подготовке кадров высшей квалификации, за рассматриваемый период заметно возросла, а «мощность» докторантур, напротив, снизилась. Выявлены некоторые территориальные особенности, отражающие различия в динамике показателей подготовки кадров высшей квалификации.
В последующей публикации [2] методами факторного анализа было выявлено, что исходное множество индикаторов состояния и динамики воспроизводства кадрового научно-инновационного потенциала российской инновационной системы может быть сведено к двум факторам – уровня и динамики числа организаций, ведущих подготовку аспирантов и докторантов.
Данная публикация носит методический характер и содержит описание этапов статистических исследований, конечная цель которых – разработка обобщенного индикатора воспроизводства кадрового научно-инновационного потенциала экономических подсистем РФ. Эмпирической базой исследований являлись временные ряды показателей воспроизводства научных кадров в федеральных округах и крупных научных центров в 2000-2009 гг., приведенные в статистическом сборнике [3], в качестве инструментария использовали пакет статистических программ SPSS Base [4].
Решение поставленной задачи затруднено тем, что число показателей воспроизводства кадрового научно-инновационного потенциала соизмеримо с объемом выборки рассматриваемых статистических единиц – федеральных округов и крупных научных центров. В соответствии с выполненными ранее исследованиями, частных индикаторов воспроизводства кадрового научно-инновационного потенциала экономических подсистем – шесть, а объем выборки – в лучшем случае, девять (семь федеральных округов плюс два региона – г. Москва и г. Санкт-Петербург. Но если разбить исследуемый временной период на два пятилетних интервала, охватывающие 2000-2004 и 2005-2009 годы, то объем выборки можно увеличить, в идеале, вдвое.
В результате такого приема сформирован следующий набор частных индикаторов – претендентов на включение в обобщенный индикатор воспроизводства кадрового научно-инновационного потенциала экономических подсистем РФ:
Х1 и Х1_дин – среднее число и среднегодовой прирост организаций в каждый пятилетний интервал, проводивших подготовку аспирантов, в расчете на млн. населения;
Х2 и Х2_дин – число организаций и среднегодовой прирост в каждый пятилетний интервал, проводивших подготовку докторантов, в расчете на млн. населения;
Х3 и Х4– средняя численность аспирантов и докторантов в каждый пятилетний интервал, приходящихся на одну организацию, ведущую подготовку аспирантов и докторантов соответственно.
В соответствии с требованиями к исходным данным, предъявляемым для обеспечения корректности статистических выводов, на первом этапе статистических исследований выполняется проверка выборки на однородность по пространственным профилям, представляющих собой последовательности, построенные для выделенных нами временных интервалов – рис. 1.
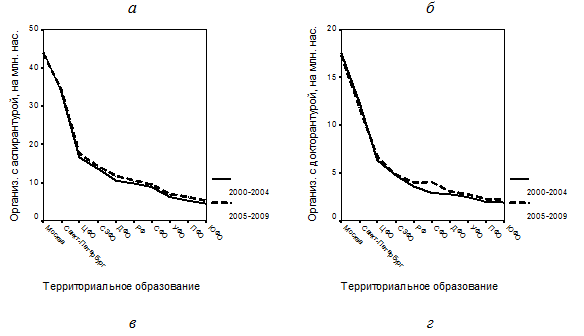
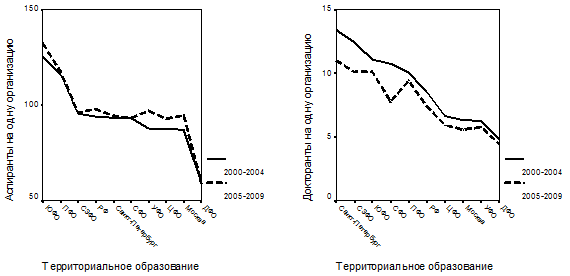
Рис. 1. Пространственные профили индикаторов воспроизводства кадрового научно-инновационного потенциала экономических подсистем РФ: а – среднее число организаций, проводивших подготовку аспирантов, в расчете на млн. населения; б – среднее число организаций, проводивших подготовку докторантов, в расчете на млн. населения; в – средняя численность аспирантов, приходящихся на одну организацию, ведущую подготовку аспирантов; г – средняя численность докторантов, приходящихся на одну организацию, ведущую подготовку докторантов
Анализ пространственных профилей, представленных на рис. 1 а и б, показывает, что г. Москву и г. Санкт-Петербург необходимо исключить из выборки экономических подсистем. Проверка данных на нормальность распределений по тесту Смирнова-Колмогорова [5] показала, что из выборки следует исключить не только эти регионы, но и Сибирский федеральный округ, в котором в период 2005-2009 гг. наблюдался резкий рост организаций с докторантурой. В результате их исключения из выборки экономических подсистем ее объем составил 13, что более чем вдвое превышает число включенных в анализ частных индикаторов, и это позволяет рассчитывать на корректность последующих статистических процедур.
Следующий этап методики – корреляционный анализ претендентов на включение в обобщенный индикатор воспроизводства кадрового научно-инновационного потенциала экономических подсистем РФ – проводили в целях выявления взаимосвязей между частными индикаторами. Результаты этого анализа представлены в табл. 1.
Таблица 1
Корреляционная матрица индикаторов воспроизводства кадрового научно-инновационного потенциала экономических подсистем РФ
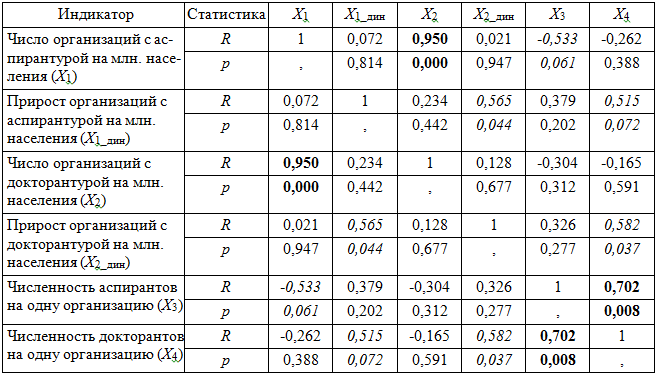
Из корреляционной матрицы следует, что между двумя парами индикаторов по однородной выборке имеются сильные связи (выделены полужирным шрифтом), а между четырьмя парами – связи средней силы (выделены курсивом). Это позволяет рассчитывать на значительное уменьшение размерности обобщенного индикатора воспроизводства кадрового научно-инновационного потенциала экономических подсистем РФ, что достигается заменой исходного множества частных индикаторов их линейными комбинациями, устанавливаемыми методами факторного анализа.
Следующий этап формирования обобщенного индикатора – факторный анализ – проводили по методу главных компонент с вращением факторов по критерию «варимакс» [6]. Основной результат факторного анализа – матрица «нагрузок» – приведен в табл. 2, где полужирным шрифтом выделены статистически значимые корреляции; в последней строке указаны доли общей дисперсии, объясняемые главными факторами; сильные корреляции выделены полужирным шрифтом.
Таблица 2
Матрица «нагрузок» исходных индикаторов воспроизводства кадрового научно-инновационного потенциала экономических подсистем РФ на главные факторы. Выборка экономических подсистем объемом N=13, данные 2000-2009 гг.
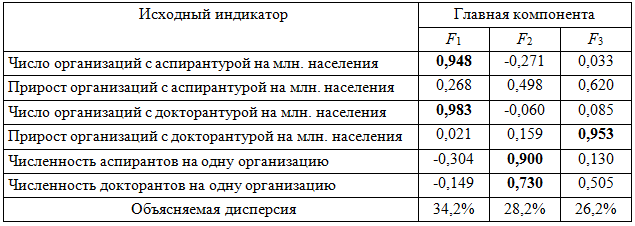
Из нижней строки табл. 2 следует, что первая главная компонента – наиболее информативная, она объясняет более трети общей дисперсии, вторая и третья компоненты менее информативны. Суммарно три главные компоненты объясняют 88,6%. Это высокий результат, и полученная трехфакторная модель структуры множества из шести исходных индикаторов может быть принята в качестве рабочей модели, а выделенные три главные компоненты можно квалифицировать как главные факторы.
Как видно из матрицы нагрузок (табл. 2), первая главная компонента F1 сильно и положительно коррелирует с двумя исходными индикаторами – числом организаций с аспирантурой на млн. населения (R=0,948) и числом организаций с докторантурой на млн. населения (R=0,983). Следовательно, первый главный фактор можно интерпретировать как «экстенсивный фактор воспроизводства кадрового научно-инновационного потенциала», и большие значения этого фактора будут предпочтительнее.
Вторая главная компонента F2 положительно коррелирует с численностью аспирантов и докторантов на одну организацию (R=0,900 и 0,730 соответственно), и ее следует интерпретировать как «интенсивный фактор воспроизводства кадрового научно-инновационного потенциала», причем предпочтительнее будут также большие значения этого фактора.
Третья главная компонента F3 положительно коррелирует с приростом организаций с докторантурой на млн. населения, и ее следует интерпретировать как «фактор динамики воспроизводства кадрового научно-инновационного потенциала».
Главные факторы – это математические конструкты, но можно их заменить наиболее сильно коррелирующими с ними частными индикаторами: первый главный фактор – числом организаций с докторантурой на млн. населения Х2, второй – численностью аспирантов на одну организацию Х3, третий главный фактор – приростом организаций с докторантурой на млн. населения Х2_дин. Из табл. 1 следует, что корреляции между этими индикаторами статистически незначимы, и они могут рассматриваться как самостоятельные компоненты обобщенного индикатора воспроизводства кадрового научно-инновационного потенциала. Еще одним преимуществом замены главных факторов частными индикаторами является возможность включить в анализ экономические подсистемы, не вошедшие в однородную выборку.
Следующий важный этап формирования обобщенного индикатора – преобразование частных индикаторов к безразмерному виду. Чаще всего для этого используется линейная шкала, согласно которой минимальное значение показателя принимается за 0, а максимальное – за 1. Однако линейное преобразование имеет много недостатков, и главное из них – оно противоречит реально существующему нелинейному характеру зависимости безразмерного индекса с оценкой значения показателя. Представляется, что в качестве нормирующего преобразования индикаторов целесообразно использовать психофизическую шкалу Харрингтона [7], которая ставит в соответствие значения формируемой на ее основе функции желательности лингвистической переменной с пятью термами: «очень плохо», «плохо», «удовлетворительно», «хорошо», «очень хорошо».
В случае монотонности функции желательности, имеющей место для индикаторов воспроизводства кадрового научно-инновационного потенциала, шкала Харрингтона выглядит следующим образом – табл. 3.
Таблица 3
Числовые интервалы шкалы Харрингтона для монотонной функции желательности
| Лингвистическая оценка (термы лингвистической переменной) | Интервалы значений функции желательностиd(x) |
| Очень плохо |
0,00-0,20 |
| Плохо |
0,20-0,37 |
| Удовлетворительно |
0,37-0,63 |
| Хорошо |
0,63-0,80 |
| Очень хорошо |
0,80-1,00 |
Практически достаточно ограничиться тремя градациями шкалы Харрингтона, отвечающим лингвистическим термам «плохо», «удовлетворительно», «хорошо». В этом случае область, соответствующая уровню «удовлетворительно», расширяется от 0,37 до 0,69, а области «плохо» и «хорошо» характеризуются интервалами (0,00-0,37) и (0,69-1,00) соответственно [8].
Аналитически функция желательности Харрингтона задается следующими формулами:
di = d (zi) = exp (-exp (-zi)), (1)
zi = (хi – хi0)/( хi1 – хi0). (2)
Здесь zi – кодированные значения i-го показателя, представляющие собой безразмерные величины; хi – значение i-го информативного показателя; хi0 и хi1 – границы области «удовлетворительно» в исходной шкале:
di0= d (zi (хi0)) = 0,37; di1= d (zi (хi1)) = 0,69. (3)
При кодированном значении информативного показателя z=0 (нижняя граница области «удовлетворительно») функция желательности принимает значение 0,368, а при z=1, что соответствует нижней границе области «удовлетворительно», d(z)=0,692. Таким образом, для построения функции желательности Харрингтона достаточно установить границы исходных показателей хi0 и хi1, внутри которых изучаемая характеристика может считаться удовлетворительной. В частности, часто эти значения полагают равными хi1=хmax и хi0=хmin, т.е. соответственно максимальному и минимальному значению показателя по массиву региональных данных.
Такой подход, однако, представляется не вполне обоснованным: при этом все рассматриваемые статистические объекты в выборке считаются «удовлетворительными», тогда как исходя из общих соображений, это не так – в любом случае есть «лидеры», есть и «аутсайдеры». Более обоснован иной подход – нижнюю границу зоны «удовлетворительно» положить равной значению параметра центральной тенденции (медианы или средней арифметической величины), а ее верхнюю зону «сдвинуть» в сторону значений показателя, отстоящих от параметра центральной тенденции на величину стандартного отклонения. Согласно правилу «трех сигм» [9], тогда примерно 1/6 часть статистических объектов будет характеризоваться термом «удовлетворительно», половина – термом «плохо», 1/3 – термом «хорошо».
Формируемая таким образом функция желательности имеет сигмоидальную форму – на начальном участке, в зоне желательности «плохо», она имеет нарастающую кривизну, т.е. даже небольшие изменения показателя приводят к заметному увеличению желательности. Напротив, в зоне «хорошо» функция имеет убывающую кривизну, так что дальнейший рост показателя уже не вызывает столь заметного увеличения желательности. В зоне «удовлетворительно» функция желательности практически линейна, и именно в этой области наблюдается максимальный эффект от увеличения показателя.
Такой сигмоидальный характер зависимости желательности от величины показателя отвечает следующим интуитивным представлениям: на начальном этапе (в зоне «плохо») важно «поощрить» рост показателя, хотя бы это и было связано со значительными затратами ресурсов разного рода, а когда значения показателя уже устраивают (зона «удовлетворительно»), нет особого смысла в дальнейшем его росте (в зоне «хорошо»), поскольку затраты при этом резко увеличиваются. Кроме того, принятие данного постулата обеспечивает четкий алгоритм построения региональных индексов. Практическое значение имеет также то, что преобразование исходных показателей с использованием психофизической шкалы Харрингтона позволяет производить расчеты частных индексов для территорий, не включенных ранее в обучающую выборку.
В нашем случае эмпирическое распределение всех трех индикаторов воспроизводства кадрового научно-инновационного потенциала по обучающей выборке экономических подсистем РФ в период 2000-2004 и 2005-2009 гг. не противоречит нормальному распределению, и для построения функций желательности использовали среднее арифметическое и стандартное отклонение (среднее квадратическое отклонение) – табл. 4.
Таблица 4
Статистика индикаторов воспроизводства кадрового научно-инновационного потенциала экономических подсистем РФ в 2000-2009 гг.
| Статистика |
Индикатор |
||
| Число организаций с докторантурой на млн. населения | Численность аспирантов на одну организацию | Прирост организаций с докторантурой на млн. населения | |
| Среднее |
9,8498 |
96,9982 |
0,0810 |
|
Стандартное отклонение |
4,57151 |
22,15225 |
0,03987 |
Принцип построения и явный вид функции желательности основного индикатора воспроизводства кадрового научно-инновационного потенциала экономических подсистем РФ – числа организаций с докторантурой на млн. населения приведен на рис. 2 (зона желательности «удовлетворительно» на диаграммах рисунка выделена пунктирными прямыми), а явный вид функций желательности двух других индикаторов – численности аспирантов на одну организацию и прироста числа организаций с докторантурой на млн. населения – на рис. 3.
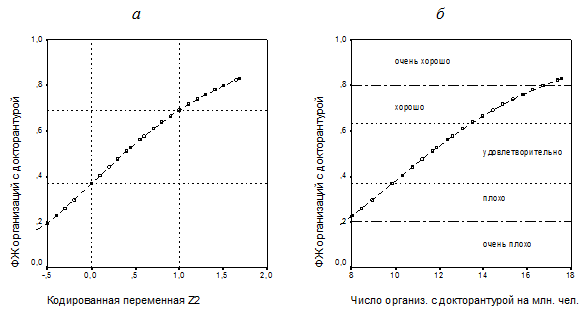
Рис. 2. Функция желательности числа организаций с докторантурой на млн. населения: а – принцип построения; б – зоны желательности
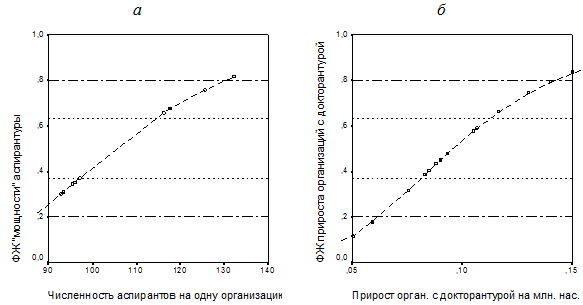
Рис. 3. Функции желательности индикаторов воспроизводства кадрового научно-инновационного потенциала экономических подсистем РФ: а – численности аспирантов на одну организацию; б – прироста числа организаций с докторантурой на млн. населения
Следующий этап – формирование обобщенной функции желательности, которая и будет индикатором воспроизводства кадрового научно-инновационного потенциала экономических подсистем РФ – проводим с учетом результатов факторного анализа.
Поскольку входящие в нее показатели, а, следовательно, и соответствующие им частные функции желательности не коррелируют или слабо коррелируют между собой, принимаем мультипликативную форму обобщенной функции желательности здоровья:
Dmult = (d1) w1 ´ (d2) w2 ´ (d3) w3, (4)
где d1, d2 и d3 – функции желательности числа организаций с докторантурой на млн. населения, численности аспирантов на одну организацию и прироста числа организаций с докторантурой на млн. населения, а wi (i=1,2,3) – веса соответствующих главных факторов, удовлетворяющие нормирующему условию
w1 +w2 +w3 = 1. (5)
Веса частных индексов в обобщенной функции желательности воспроизводства кадрового научно-инновационного потенциала экономических подсистем РФ целесообразно принять пропорциональными долям дисперсии, объясняемой соответствующими главными факторами. Первый главный фактор F1 – экстенсивный фактор воспроизводства кадрового научно-инновационного потенциала – объясняет 34,2% общей дисперсии, второй – интенсивный фактор воспроизводства кадрового научно-инновационного потенциала F2 – 28,2%, третий – фактор динамики воспроизводства кадрового научно-инновационного потенциала F3 – 26,2%, и с учетом (5) получаем:
w1 = 34,2/88,6 = 0,386; w2 = 28,2/88,6 = 0,318; w3 = 26,2/88,6 = 0,296.
Таким образом, формула (4) для расчета обобщенной функции желательности воспроизводства кадрового научно-инновационного потенциала принимает следующий вид:
Dmult = d10,386 ´ d20,318 ´ d30,296. (6)
Наряду с мультипликативной формой регионального индекса воспроизводства кадрового научно-инновационного потенциала, рассмотрим также аддитивную форму индекса, определяемую формулой
Dadd = 0,386d1 + 0,318d2 + 0,296d3. (7)
Согласно теории измерений, формула (6) дает жесткую – пессимистическую оценку регионального индекса воспроизводства кадрового научно-инновационного потенциала, формула (7) – более мягкую, оптимистическую.
Наряду с пессимистическими и оптимистическими оценками, целесообразно рассмотреть взвешенную оценку обобщенного индекса воспроизводства кадрового научно-инновационного потенциала по критерию Гурвица, учитывающему степень оптимизма l:
Dвзвеш= l ´ Dadd + (1 – l) ´ Dmult. (8)
Взвешенная оценка обобщенного индекса отвечает значению степени оптимизма l=0,5; при наличии на то оснований, исследователь вправе установить и иные значения степени оптимизма, например, l=0,75.
Ранжирование экономических систем по взвешенной оценке обобщенного индекса воспроизводства кадрового научно-инновационного потенциала в два периода – 2000-2005 и 2005-2009 гг. – представлено на рис. 4.
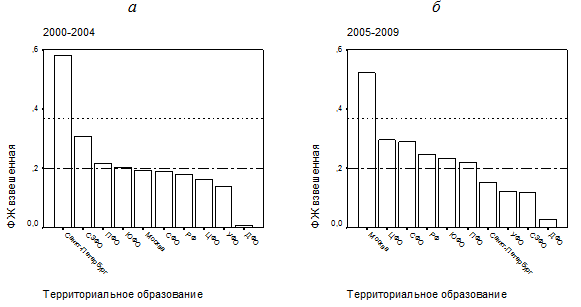
Рис. 4. Ранжирование экономических подсистем РФ по взвешенной оценке обобщенного индекса воспроизводства кадрового научно-инновационного потенциала: а – 2000-2004 гг.; б – 2005-2009 гг.
Судя по рис. 4, ситуация в области воспроизводства кадрового научно-инновационного потенциала РФ является тревожной – в 2000-2004 гг. только г. Санкт-Петербург получает оценку «удовлетворительно», а в 2005-2009 гг. такую же оценку получает г. Москва. Большинство же экономических подсистем, как и Российская Федерация в целом, характеризуются оценками «плохо» и «очень плохо».
Понятно, что оценки «очень плохо», «плохо», «удовлетворительно» здесь надо понимать не абсолютно, а относительно. Однако представленные результаты симптоматичны, и дают федеральным и региональным органам управления возможность проводить мониторинг индикаторов воспроизводства кадрового научно-инновационного потенциала экономических подсистем РФ, разрабатывать предложения по повышению инновационного потенциала регионов и страны в целом.
Читайте также
Библиографический список
- Котельников С.А. Территориальное распределение и динамика показателей кадрового научного потенциала российской инновационной системы. «Перспективы науки»/ журнал. 2011 год.
-
Котельников С. А. Индикаторы состояния и развития системы подготовки научных кадров в федеральных округах и крупных научных центрах Российской Федерации//Современные технологии управления. ISSN 2226-9339. — №3 (15). Номер статьи: 1505. Дата публикации: 2012-03-08 . Режим доступа: https://sovman.ru/article/1505/
-
Регионы России. Социально-экономические показатели. 2010. Стат. сб. / Росстат. М., 2010.
- SPSS Base 8.0 для Windows. Руководство по применению. Перевод–Copyright 1998 СПСС Русь.
- Бююль А., Цёфель П. SPSS: Искусство обработки информации. Анализ статистических данных и восстановление скрытых закономерностей. СПб.: ООО «ДиаСофтЮП», 2002.
- Факторный, дискриминантный и кластерный анализ / Дж.-О. Ким, Ч.И. Мьюллер, У.Р. Клекка и др.; Под ред. И.С. Енюкова. М.: Финансы и статистика, 1989.
- Harrington E.C. The desirable function // Industrial Quality Control. 1965. V.21. №10.
- Оптимизация качества. Сложные продукты и процессы / Э.В. Калинина, А.Г. Лапига, В.В. Поляков и др. М.: Химия, 1989.
- Статистика. Учебник / Под ред. И.И. Елисеевой. М.: ООО «ВИТРЭМ», 2002.
References
- Kotelnikov S.A. Spatial distribution and dynamics of human scientific potential of the Russian innovation system
-
Kotel’nikov S.A. Status and development of scientific training in the federal districts and major research centers in the Russian Federation// Современные технологии управления. ISSN 2226-9339. – #3 (15). Номер статьи: 1505. Дата публикации: 2012-03-08 . Режим доступа: http://sovman.ru/en/article/1505/
- Regions of Russia. Socio-economic indicators. 2010. Stat. Sat / Rosstat. Moscow, 2010.
- SPSS Base 8.0 for Windows. Application manual. Translation-Copyright 1998 JCSS Russia.
- Byuyul A., P. Tsefel SPSS: The Art of information processing. Statistical data analysis and recovery of hidden patterns. SPb.: LLC “DiaSoftYuP”, 2002.
- Factor, discriminant and cluster analysis / Dzh.-O. Kim CH.I. Myuller, WR Klekka and others, ed. IS Enyukova. Moscow: Finance and Statistics, 1989.
- Harrington E.C. The desirable function / / Industrial Quality Control. 1965. V.21. Number 10.
- Quality optimization. Sophisticated products and processes / E.V. Kalinin, A. Lapiga, V.V. Poles and other Khimiya, 1989.
- Statistics. Tutorial / Ed. I.I. Eliseev. Moscow: OOO “VITREM”, 2002.






