Моделирование структурной динамики в макроэкономическом анализе
Modeling structural dynamics in macroeconomic analysis
Авторы
Аннотация
В настоящей статье исследуется вычислительные возможности конкурентных моделей структурной динамики в макроэкономике. Такие модели формализуются системами обыкновенных дифференциальных уравнений или их разностными аналогами с шагом дискретизации расчетной области 1 год. Обе модели представляют собой динамический межотраслевой баланс. Теоретически всегда считается, что такие модели равноправны при использовании в численном анализе переходных процессов. Достигнуты две цели исследования. Во-первых, обосновано преимущество дифференциальных уравнений в отношении точности получаемого прогноза. Во-вторых, показаны принципиальные ограничения разностных аналогов в решении многих задач устойчивости, экономической динамики, экономического роста и управления ими на основе вычисления показателей собственных, то есть внутренних, динамических свойств экономики как системы. Такие свойства вычисляются для математически замкнутых по потреблению динамических межотраслевых балансов. Обсуждаемые модели используются в макроэкономическом анализе, анализе экономик региона и могут быть интегрированы в состав вычислительных систем, представляемых равновесными или иными агент-ориентированными моделями.
Ключевые слова
моделирование, структурная динамика, межотраслевой баланс, дифференциальные уравнения, погрешности вычислений, экономический рост.
Финансирование
Статья подготовлена при финансовой поддержке РФФИ. Грант № 20-010-00084А. «Математическое моделирование структурной устойчивости и макроэкономической динамики».
Рекомендуемая ссылка
No items found. Моделирование структурной динамики в макроэкономическом анализе // Современные технологии управления. ISSN 2226-9339. — №2 (92). Номер статьи: 9221. Дата публикации: 02.08.2020. Режим доступа: https://sovman.ru/article/9221/
Authors
Abstract
This article explores the computing capability of competitive models of structural dynamics in macroeconomics. These models are formalized by systems of ordinary differential equations or their differential analogues with a discretization step of the calculated range of 1 year. Both models represent a dynamic input-output balance. Theoretically, these models are always considered equal when used in the numerical analysis of transients. Two research objectives have been achieved. Firstly, the advantage has been proved for differential equations regarding to the accuracy of the forecast obtained. Secondly, the fundamental limitations of differential analogues are shown in solving many problems concerning sustainability, economic dynamics, economic growth and their management based on the calculating indicators of the own, that is, internal, dynamic properties of the economy as a system. Such properties are calculated for dynamic input-output balances mathematically real-closed by consumption. The discussed models can be applied in macroeconomic analysis either independently or as part of larger computing systems represented by equilibrium or other agent-based models.
Keywords
Modeling, structural dynamics, input-output balance, differential equations, calculation errors, economic growth
Project finance
The article was prepared with the financial support of the Russian Foundation for Basic Research. Grant № 20-010-00084А "Mathematical modeling of stability and macroeconomic dynamics".
Suggested citation
No items found. Modeling structural dynamics in macroeconomic analysis // Modern Management Technology. ISSN 2226-9339. — №2 (92). Art. # 9221. Date issued: 02.08.2020. Available at: https://sovman.ru/article/9221/
Введение
Необходимость проведения масштабных структурных реформ в российской экономике декларируются и обосновываются самыми авторитетными научными кругами и правительством. Примеры тому можно видеть в [1, 2]. А какая структура экономики является желательной? Ответы на этот вопрос естественным образом разнятся. Кому-то комфортно в условиях макроэкономической стабильности и низкой инфляции, а другие считают это совершенно недостаточным для всех проявлений успешности страны [2].
Мы будем обсуждать вопросы экономической динамики, формирующейся в результате реализации действительно структурных реформ. В математических моделях эти процессы формализуются дифференциальными уравнениями (ДУ) или их разностными аналогами. Теоретически это конкурирующие модели, однако в задачах экономического анализа и прогнозирования ДУ пока ещё не нашли достойного применения и признания.
Между тем, модели на основе ДУ естественным образом приспособлены для решения многочисленных задач структурной устойчивости, экономической динамики и экономического роста на основе таких вычислимых характеристик, как показатели собственных динамических свойств (СДС) макроэкономики. Здесь понятие «собственных» означает «внутренних», присущих структуре системы. К числу показателей СДС относятся частоты и затухания отдельных составляющих движения в переходном процессе, их управляемости, наблюдаемости и возбуждаемости в отдельных видах экономической деятельности (ВЭД), другие их системные характеристики. Для заинтересованного читателя делаем ссылку1.
Уже скоро семь десятилетий минует с того времени, как моделирование структурной динамики и связанного с ней экономического роста (или спада) В. В. Леонтьевым и его коллегами-учениками было возложено «на плечи» динамического межотраслевого баланса (МОБ). Мы имеем в виду работу [3], в которой динамический МОБ приведён в виде
(1)
где 
— оператор дифференцирования по времени; 
— матрица межотраслевых инерционностей, элементы которой имеют размерность времени; 
— технологическая матрица коэффициентов текущих/прямых производственных затрат; 
— вектор-функция валовых выпусков по видам экономической деятельности (ВЭД); 
— вектор-функция конечного спроса. Эту модель В. В. Леонтьев записал в 1952 г., и уже в середине 1950-х гг. динамическая теория «затраты-выпуск» проходила первую эмпирическую проверку в США.
В разных источниках нам приходилось видеть ссылки на модель (1), однако в оцифрованном виде, позволяющем воспроизвести расчёты и сделать новые, эта модель нигде не приведена. В России к модели (1) и вовсе специфическое отношение – она всегда относилась и теперь привычно относится к семейству «чисто теоретических конструкций», как это отмечено, например, в [4]. Между тем, модель (1) при её замыкании по потреблению оказывается, в отличие от разностных аналогов, наилучшим образом адекватной задаче определения показателей СДС экономики, играющих важную роль для исследования проблем структурной устойчивости, качества структурных реформ и управления ими.
Например, вычисление степени экономического роста позволяет ответить на вопрос о технологической готовности или неготовности экономики к расширенному воспроизводству. В случае положительного ответа на вопрос и отсутствии роста, так же, как и при неадекватном фактическом росте в зоне очень малых приращений, проблему надо искать в контуре управления системой. Показатели наблюдаемости, управляемости/чувствительности и возбуждаемости компонент движения в ВЭД дают обоснования для разработки структурных реформ и организации инвестиционных процессов с целью стимулирования экономического роста на основе математически строгого определения степени влияния инвестиций на этот рост.
Здесь надо иметь в виду, что для осуществления планов «прорывного экономического роста» требуется выполнение как необходимых, так и достаточных условий – это как в математике. Только что мы сказали о необходимых: экономика по своим структурным свойствам должна быть управляемой и, так сказать, «ростопригодной». Приводить её в такое состояние – дело лиц, принимающих экономические решения (ЛПР). Достаточные же условия формируются всё в том же в контуре управления за счёт проведения этим контуром денежно-промышленной и всей иной политики, соответствующей масштабам задач развития. В начале 2020 г. мы стали свидетелями отставки правительства и формирования нового. Это воспринимается в качестве ключевого элемента алгоритма настройки обсуждаемого контура. Таким образом, выполнение достаточных условий для роста экономики – прямая задача лиц, занимающих должности региональных и федеральных министров, а также Банка России. Не секрет, что Правительство и Банк в последние годы сталкивались всё с новыми и новыми волнами обоснованной критики со стороны разных экспертных сообществ. Мы не будем здесь развивать эту тему, а только поделимся своим ощущением того, что многим пока ещё действующим чиновникам не по плечу решение серьёзных экономических задач. Они или не умеют их решать или просто боятся этого. Вероятнее второе. А ограничение своего функционала требованиями со стороны населения в том или ином виде и проведение запланированной «ценоповышательной» экономической политики ставит под сомнение выход на желаемые темпы роста. С января 2019 г. ожидания россиян во многом связаны с новым российским Правительством.
Результаты исследований
Переходя к анализу влияния структурной динамики на экономический рост, отметим близкую родственность этих понятий. Структурная динамика, отображаемая структурными же моделями, в конечном счёте, визуализирует валовые выпуски в разрезе ВЭД. Экономический рост с 1934 г. измеряется как рост ВВП. А от валовых выпусков до ВВП путь прямой – вот и родственность. Потому структурная динамика и структурные реформы воспринимаются социумом как в качестве меры оценки трансформаций экономической жизни, так и в качестве инструментария механизмов развития.
Далее надо отметить, что содержание структурных реформ в странах G7, например, заключается в манипулировании основными макроэкономическими пропорциями при реализации положений экономической политики. Это значит, что денежно-кредитная, налоговая, бюджетная и т.п. системы меняют свои параметры с целью заданного перераспределения доходов между экономическими агентами. Российский контур управления, используя метод «по аналогии», часто видит задачи структурного реформирования в перераспределении ресурсов между государством, бизнесом, домашними хозяйствами и иными агентами. Это же просто! Но такое использование мирового опыта применительно к экономике России неправомерно, ошибочно! В самом деле, недолгий анализ статистики позволяет видеть, что в упомянутой группе стран уже на протяжении десятка лет не происходит существенного изменения отраслевой структуры экономики. Это и позволяет там сосредоточиться на максимизации функций полезности за счёт варьирования основных макроэкономических пропорций.
Совсем не так развивается Россия, где в последние 25 лет масштабы и скорость трансформаций отраслевой структуры в значительной мере определяли изменения показателей доходов и цен. Таким образом, при моделировании для G7 производство вообще можно представить как в модели Р. Солоу, одной обобщённой отраслью, производящей один универсальный продукт, который может как инвестироваться, так и потребляться, при детальном представлении научно-технического прогресса, монетарного сектора, торговли и сектора услуг вообще. Что же, для стран G7 так поступать можно. Наверное поэтому они в своё время позволили себе уйти от широкого использования МОБ в анализе макроэкономики. Это несколько повышает скорость анализа за счёт уменьшения его глубины. При моделировании для России модель (1) со всей возможной гаммой ВЭД играет ключевую роль. Для России в высшей мере актуальны качественные изменения в структуре производства, их анализ на основе МОБ, в том числе и оценка затрат ресурсов на эти изменения.
Модель (1) может заменить традиционное статическое уравнение МОБ во многих, если не во всех, вычислительных комплексах/системах, реализующих программно-аналитический инструментарий разработки и оценки эффективности экономической политики, проводимой в стране. Мы имеем в виду, прежде всего, межотраслевые динамические модели RIM [5] и QUMMIR [6], разработанные в ИНП РАН, а также вычислимые модели общего равновесия CGE из ЦЭМИ РАН [7].
Все упомянутые модели вычислимы, то есть количественно определены, и предоставляют числовые оценки действий или бездействий в контуре управления. Они сопровождают и прогнозируют развитие экономики, отвечая на вопрос: «Каковы последствия реализации той или иной экономической политики?» Качество статистической базы исследований, информационно-аналитические возможности программных комплексов и выполненные расчёты могут оказывать непосредственное влияние на принятие управленческих решений. Но «влияние» происходит только тогда, когда в контуре управления проявляют интерес к подобным исследованиям и хотят использовать их результаты. В этом случае прогнозно-аналитический инструментарий будет практически полезным, в числовом виде предоставляющим аргументы, обоснования и мотивировки для ЛПР. В целом это послужит лучшему выбору варианта экономической политики, что отмечается в [8].
Для дальнейшего изложения необходимо определиться с положениями, которым должен удовлетворять экономический прогнозно-аналитический инструментарий. Во-первых, он должен быть адекватным решаемым задачам в реальной экономике. Во-вторых, необходимо дать ответ на вопрос о теоретических и временных границах и условиях применимости предлагаемых моделей. В-третьих, модели должны быть эконометрически определены, значит оцифрованы как на основе данных генерируемых Росстатом массивов, так и на основе собственной статистической базы исследований. Последнее не обязательно, но возможно. Причём собственная база должна быть проверяемой, логичной, восстановимой и должна наполнять модели данными, которые официальная статистика не производит. Анализ трёх указанных положений позволяет выявить достаточность моделирования в линейной парадигме, или установить необходимость привлечения некоторых нелинейных зависимостей. Также можно определить в какой мере данные и эконометрические зависимости, полученные для экономик одних стран, могут быть использованы для анализа и прогнозирования в условиях других экономик и стран.
Привлекаемый модельный инструментарий, с одной стороны, отражает вкусы, взгляды и предпочтения самих исследователей, а с другой ориентируется на современные теоретико-методологические основания науки. Последние в абсолютном большинстве случаев опираются либо на Новый неоклассический синтез (или просто Новый синтез), как на слияние Новой классики и Нового кейнсианства, либо просто на старенькую уже (здесь 1870-е годы рождения и восхождение к Л. Вальрасу) неоклассическую парадигму. В качестве примера обращения к первой теоретической школе можно сослаться на работы [9] и [10], представляющие агент-ориентированные модели – они в настоящее время активно развиваются. Сошлёмся в этом случае на АОМММ – агент-ориентированную многорегиональную модель «затраты-выпуск» ИЭОПП СО РАН, научный руководитель чл.-корр. РАН В.И. Суслов.
Лучшие примеры, опирающиеся на вторую школу [7] и [11] и подобные им, вышли в ЦЭМИ РАН из-под пера В.Л. Макарова, А.Р. Бахтизина и их соавторов – это не менее активно развивающееся направление. Оно представляется вычислимыми моделями общего равновесия (CGE-моделями) и динамическими стохастическими моделями общего равновесия (DSGE-моделями). Оба направления в моделировании подчёркивают связь с межотраслевым анализом, способны исследовать процессы производства, распределения, перераспределения и конечного использования доходов, товаров и услуг агентов и институциональных единиц, включённых в модель. Для этого модели инкорпорируют в себя таблицы «затраты-выпуск» и/или матрицы социальных счетов (SAM-матрицы).
Оба класса моделей в состоянии повысить свои прогнозно-аналитические возможности на основе не только упомянутых таблиц, но и за счёт прямого включения модели (1) с блоком интегрирования и расчёта СДС. Более того, модели, построенные на теоретических положениях неоклассики не должны применяться безоговорочно и автоматически. Мы имеем в виду, например, CGE-модели [12,13], которые нуждаются в выполнении условий их корректной применимости в конкретных схемно-режимных условиях функционирования экономики как системы. И это утверждение не преодолевается заверениями разработчиков о масштабных возможностях и самодостаточности данных моделей при решении отводимого им круга задач. Не повышает меры доверия к результатам моделирования на основе CGE и указание на то, что модели строятся на основе «экономически обоснованных» зависимостей [13]. Ведь сразу возникает естественный вопрос: «А существуют ли границы, до которых экономическая обоснованность сохраняется, а за этими границами утрачивается?» Ответ на этот вопрос выглядит так: такие границы существуют и обусловлены они ограничениями теоретико-методологической базы, на которой построены модели [14]. А каковы же базовые положения неоклассики? Эти положения, как и положения многих других теорий, представляют реальную экономику как некоторую идеализированную систему, где, например, набор ресурсов и услуг распределяется между конкурирующими направлениями использования с неким оптимальным результатом, что идентифицируется термином «маржинализм». Кроме того, достижимым считается состояние общего равновесия, то есть между спросом и предложением, производством и потреблением, потенциальным и номинальным выпуском и т.п., выбор и ожидания индивидов рациональны, а их предпочтения стабильны [15]. А ещё в экономике доминирует совершенная конкуренция, работает принцип соответствия Самуэльсона, сравнительная статика, в обществе царят политическая свобода и социальная справедливость. Более полное описание положений неоклассики можно видеть в учебниках по экономической теории. Однако и того, что сказано здесь, достаточно для снижения, а иногда и утраты доверия к результатам вычислительных экспериментов с равновесными моделями.
Нахождение в плену неоклассической теории часто рассматривается авторами CGE в качестве их достоинства [8]. Ровно так же подчёркивается высокая значимость соединения микро- и макроэкономических подходов в моделировании [16]. Это делается без оглядки на очевидность того, что в рамки неоклассики реальная экономическая картина России и мира вписывается далеко не всегда. Сказанное требует выполнения необходимых и достаточных условий корректного применения CGE-моделей. Выполнение указанных условий сводится, в конечном счёте, к тому, что равновесные модели могут быть рекомендованы для прогнозирования и решения иных задач в отношении экономик, которые устойчиво развиваются на длинных временных горизонтах [17]. Стагнирующие (этим термином характеризуют состояние экономики современной России, во всяком случае, на интервале 2013-2019 гг.), и саморазрушающиеся экономические системы (это характеристика траектории «развития», на которой в известное время новейшей истории также пребывала экономика России) не нуждаются в определении равновесных точек или траекторий. Определение равновесия в таких условиях бессмысленно и бесполезно. Единственной достойной целью функционирования экономики может быть перевод её на магистральные темпы роста при росте производительности, конкурентоспособности и всех иных составляющих эффективности. Только такая экономическая динамика через время 
позволит сойти с магистрали, например, для достижения целей социальной политики, связанных с перераспределением благ и качественным повышением уровня благосостояния населения. Это прямо означает, что общественные ожидания роста благосостояния в самой ближней перспективе, просто в связи со сменой Председателя и ряда членов правительства, неоправданно и необоснованно. Рост благосостояния при нахождении экономики на луче Неймана возможен, но только невысокими темпами. Магистраль предполагает опережающий рост нормы накопления основного капитала предприятий, доминирующие инвестиции в него и в инфраструктуру. А вот запланированный сход с магистрали должен быть сопряжён с почти скачкообразным ростом благосостояния, но с условием последующего возвращения в конус магистральных траекторий, вхождения в новый цикл экономического развития и роста.
Технологическую или структурную готовность экономики к расширенному воспроизводству устанавливает анализ СДС на основе модели (1). Для решения этой задачи, в том числе и для определения количественных характеристик возможного роста, модель приспособлена, как уже отмечалось, по своей природе. При этом интегрирование переходного процесса целесообразно путём вычисления матричной экспоненты и её интеграла. Разностные аналоги однозначно проигрывают этим вычислительным процедурам по точности прогноза. В самом деле, замена системы дифференциальных уравнений (1) разностным аналогом при замыкании модели по потреблению приводит к рекуррентной форме метода Эйлера
(2)
который устойчив в вычислительном отношении, но обладает только первым порядком точности. Естественно, что погрешность растёт с увеличением горизонта прогнозирования и темпа экономического роста, что показано на рис. 1 ниже. Покажем это на примере численного расчёта с использованием непрерывной и разностной модели. Рассматривать будем только один ВЭД – «Добыча полезных ископаемых» из раздела «В» ОКВЭД-2. При этом для непрерывного случая задача аппроксимации решалась путём вычисления матричной экспоненты и её интеграла, а высокая точность расчёта достигалась увеличением числа членов равномерно сходящихся рядов для определения этих объектов. В качестве начальных условий для обеих моделей использовались данные 2014 года, то есть 
.
На рис. 1 представлен результат аппроксимации заявленного валового выпуска для двух исследуемых моделей. Процесс непрерывного интегрирования со стартового года представляют сплошные линии. Расчёты по формуле (2) отображены крестиками синего цвета, соединёнными пунктиром. Степень или темп роста для двух вариантов интегрирования и выбранного ВЭД есть величина вычислимая: в нашем случае 
.
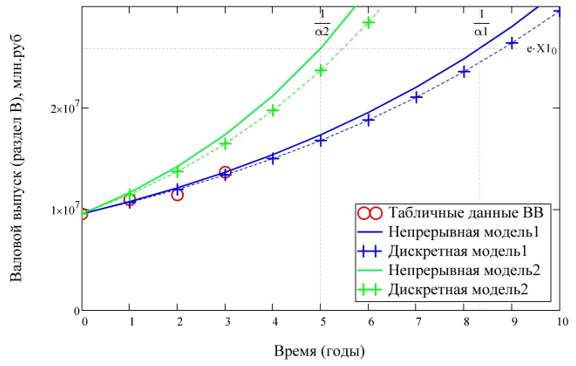
Рис. 1. Моделирование выпуска ВЭД «Добыча полезных ископаемых»
Из рисунка видно как разностная схема накапливает ошибку. Например, можно точно определить момент увеличения выпуска, скажем, в e раз, как показано на рисунке, при построении непрерывного решения, что недоступно разностному решению. Природа ошибок разностных схем для обыкновенных ДУ исследуется в соответствующих учебниках и пособиях. Здесь же отметим рост ошибки аппроксимации решения ДУ разностной схемой с увеличением темпа/степени роста экономики до 
на том же рисунке – кривые зелёного цвета.
В качестве общего вывода следует отметить, что разностные схемы с шагом дискретизации расчётной области в 1 год надо с осторожностью применять для прогнозирования, даже среднесрочного. Правда, можно откалибровать разностную схему таким образом, что оба рассматриваемых решения совпадут, однако модель при этом утратит экономическую трактовку своих параметров и превратится в имитационную.
Поясним сказанное на примере модели из одного ДУ, включив конечный спрос в первое слагаемое правой части:
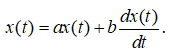(3)
Нормальная форма Коши
, (4)
позволяет записать решение
(5)
Дискретный аналог уравнения (3) при шаге по времени, равном 1 году, имеет вид:
(6)
Запись уравнения (6), удобная для прогнозирования
(7)
даёт решение (7), являющееся аналогом (5). Как видим, модели (3), (4) и (6), (7) имеют одну и ту же степень роста 
, но результаты счёта будут разными, что отражено на рис.1. Калибровка разностной модели для совпадения результатов счёта по двум моделям изменит значения, а значит и экономическое содержание её параметров.
Приведённые рассуждения на примере одного дифференциального уравнения, а не на примере системы размерности 
сделаны только для того, чтобы читателю было проще разобраться в вынесенной на обсуждение теме.
Ещё больший недостаток использования разностных схем при моделировании заключается в невозможности исчисления показателей СДС. Они предназначены только для визуализации переходного процесса.
Заключение
Завершая изложение, мы рады сообщить заинтересованному читателю об успешном решении нами проблемы оцифровки модели (1), то есть о состоявшемся (впервые в экономической науке) переводе её из множества «теоретических», предлагаемый в лучшем случае студентам в лабораторных практикумах, во множество вычислимых, то есть прикладных моделей [18].
_______________
1 Торопцев Е.Л., Таточенко Т.А. Теоретические основы управления модернизацией и экономическим ростом // Региональная экономика: теория и практика. – 2011. – №. 2(185). – С. 2-11. https://www.fin-izdat.ru/journal/region/detail.php?ID=35144
Читайте также
Библиографический список
- Трансформация структуры экономики: механизмы и управление: монография / Под науч. ред. А.А. Широва. Москва: МАКС Пресс, 2018.
- Структурно-инвестиционная политика в целях обеспечения экономического роста в России: монография / Под науч. ред. акад. В.В. Ивантера. – М.: Научный консультант. – 2017.
- Леонтьев В.В. Экономические эссе. Теории, исследования, факты и политика. М.: Политическая литература, 1990.
- Суворов Н.В., Трещина С.В., Балашова Е.В., Давидкова О.Б., Зенкова Г.В. Роль технологического фактора в развитии российской экономики: результаты прогнозно-аналитических исследований // Научные труды: Институт народнохозяйственного прогнозирования РАН. М.: МАКС Пресс, 2015. С. 8–76.
- Серебряков Г.Р. Опыт построения динамической межотраслевой равновесной модели российской экономики // Проблемы прогнозирования. 2000, № 2. С. 3–19.
- Савчишина К.Е. Прогнозирование показателей налогово-бюджетной сферы в рамках квартальной макроэкономической модели QUMMIR. // Научные труды: Институт народнохозяйственного прогнозирования РАН. 2008, №6. С. 225–241
- Макаров В.Л., Бахтизин А.Р., Сулакшин С.С. Применение вычислимых моделей в государственном управлении. М.: Научный эксперт, 2007.
- Широв А.А. Роль инструментальных методов анализа и прогнозирования при обосновании экономической политики // Проблемы прогнозирования. 2017, № 2(161). С. 3–9.
- Суслов В.И., Доможиров Д.А., Ибрагимов Н.М., Костин В.С., Мельникова Л.В., Цыплаков А.А. Агент-ориентированная многорегиональная модель «затраты-выпуск» российской экономики // Экономика и математические методы. 2016. Т. 52, № 1. С. 112–131.
- Суслов В.И., Новикова Т.С., Цыплаков А.А. Моделирование роли государства в пространственной агент-ориентированной модели // Экономика региона. 2016. Т. 12, № 3. С. 951–965.
- Макаров В.Л., Бахтизин А.Р. Социальное моделирование – новый компьютерный прорыв (агент-ориентированные модели). М.: Экономика. 2013.
- Изотов Д.А. Эмпирические модели общего экономического равновесия // Пространственная экономика. 2014. № 3. С. 138–167.
- Макаров В.Л., Бахтизин А.Р., Сулакшин С.С. Применение вычислимых моделей в государственном управлении. М.: Научный эксперт, 2007.
- Грассини М. Проблемы применения вычислимых моделей общего равновесия для прогнозирования экономической динамики // Проблемы прогнозирования. 2009. № 2. C. 30–47.
- Ельшин Л.А. Методические подходы к прогнозированию промышленного развития на основе построения ожиданий экономических агентов // Экономический анализ: теория и практика. 2017. Т.16, вып.11, С. 2028–2042.
- Wang K., Wang C., Chen J. Analysis of the Economic Impact of Different Chinese Climate Policy Options Based on a CGE Model Incorporating Endogenous Technological Change // Energy Policy. 2009. Vol. 37. No. 8. Pp. 2930–2940. DOI: 10.1016/j. enpol.2009.03.023.
- Любушин Н.П., Бабичева Н.Э., Усачев Д.Г., Шустова М.Н. Генезис понятия «устойчивое развитие экономических систем различных иерархических уровней» // Региональная экономика: теория и практика. 2015. № 48. С. 2–14.
- Торопцев Е.Л., Мараховский А.С., Дужински Р.Р. Проблема оцифровки динамической модели межотраслевого баланса // Экономический анализ: теория и практика. – 2020. – Т. 19, № 5. – С. 946 – 972. https://doi.org/10.24891ea.19.5.946
References
- Transformation of the structure of the economy: mechanisms and management: monograph [Transformatsiya struktury ekonomiki: mekhanizmy i upravleniye: monografiya]/ Under scientific. ed. A.A. Shirov. Moscow: MAKS Press, 2018.
- Structural and investment policy in order to ensure economic growth in Russia: monograph [Strukturno-investitsionnaya politika v tselyakh obespecheniya ekonomicheskogo rosta v Rossii: monografiya]/ Under scientific. ed. acad. V.V. Ivanter. – M .: Scientific consultant. – 2017.
- Leont’yev V.V. Economic essays. Theory, Research, Facts and Politics [Ekonomicheskiye esse. Teorii, issledovaniya, fakty i politika]. Moscow: Political Literature, 1990.
- Suvorov N.V., Treshchina S.V., Balashova Ye.V., Davidkova O.B., Zenkova G.V. The role of the technological factor in the development of the Russian economy: the results of predictive and analytical research [Rol’ tekhnologicheskogo faktora v razvitii rossiyskoy ekonomiki: rezul’taty prognozno-analiticheskikh issledovaniy /]// Scientific works: Institute of National Economic Forecasting RAS. Moscow: MAKS Press, 2015. P. 8–76.
- Serebryakov G.R. Experience of building a dynamic intersectoral equilibrium model of the Russian economy [Opyt postroyeniya dinamicheskoy mezhotraslevoy ravnovesnoy modeli rossiyskoy ekonomiki]// Problems of forecasting. 2000, No. 2. P. 3–19.
- Savchishina K.Ye. Forecasting the indicators of the fiscal sphere within the framework of the quarterly macroeconomic model QUMMIR. [Prognozirovaniye pokazateley nalogovo-byudzhetnoy sfery v ramkakh kvartal’noy makroekonomicheskoy modeli QUMMIR]// Scientific works: Institute of National Economic Forecasting, RAS. 2008, no. 6. P. 225-241
- Makarov V.L., Bakhtizin A.R., Sulakshin S.S. Application of computable models in public administration [Primeneniye vychislimykh modeley v gosudarstvennom upravlenii]. Moscow: Scientific expert, 2007.
- Shirov A.A. The role of instrumental methods of analysis and forecasting in substantiating economic policy [Rol’ instrumental’nykh metodov analiza i prognozirovaniya pri obosnovanii ekonomicheskoy politiki]// Problems of forecasting. 2017, No. 2 (161). S. 3-9.
- Suslov V.I., Domozhirov D.A., Ibragimov N.M., Kostin V.S., Mel’nikova L.V., Tsyplakov A.A. Agent-based multiregional input-output model of the Russian economy [Agent-oriyentirovannaya mnogoregional’naya model’ «zatraty-vypusk» rossiyskoy ekonomiki]// Economics and Mathematical Methods. 2016.Vol. 52, No. 1. P. 112–131.
- Suslov V.I., Novikova T.S., Tsyplakov A.A. Modeling the role of the state in a spatial agent-based model [Modelirovaniye roli gosudarstva v prostranstvennoy agent-oriyentirovannoy modeli]// Economy of the region. 2016.Vol. 12, No. 3, pp. 951–965.
- Makarov V.L., Bakhtizin A.R. Social modeling is a new computer breakthrough (agent-based models) [Sotsial’noye modelirovaniye – novyy komp’yuternyy proryv (agent-oriyentirovannyye modeli)]. M .: Economics. 2013.
- Izotov D.A. Empirical models of general economic equilibrium [Empiricheskiye modeli obshchego ekonomicheskogo ravnovesiya]// Spatial Economics. 2014. No. 3. P. 138–167.
- Makarov V.L., Bakhtizin A.R., Sulakshin S.S. Application of computable models in public administration [Primeneniye vychislimykh modeley v gosudarstvennom upravlenii]. M .: Scientific expert, 2007.
- Grassini M.Problems of using computable general equilibrium models for forecasting economic dynamics [Problemy primeneniya vychislimykh modeley obshchego ravnovesiya dlya prognozirovaniya ekonomicheskoy dinamiki]// Problems of forecasting. 2009. No. 2. P. 30–47.
- Yel’shin L.A. Methodological approaches to forecasting industrial development based on the construction of expectations of economic agents [Metodicheskiye podkhody k prognozirovaniyu promyshlennogo razvitiya na osnove postroyeniya ozhidaniy ekonomicheskikh agentov]// Economic analysis: theory and practice. 2017. Vol. 16, issue 11, pp. 2028–2042.
- Wang K., Wang C., Chen J. Analysis of the Economic Impact of Different Chi¬nese Climate Policy Options Based on a CGE Model Incorporating Endogenous Tech¬nological Change // Energy Policy. 2009. Vol. 37. No. 8. Pp. 2930-2940. DOI: 10.1016 / j. enpol. 2009.03.023.
- Lyubushin N.P., Babicheva N.E., Usachev D.G., Shustova M.N. Genesis of the concept of “sustainable development of economic systems of various hierarchical levels” [Genezis ponyatiya «ustoychivoye razvitiye ekonomicheskikh sistem razlichnykh iyerarkhicheskikh urovney»]// Regional economy: theory and practice. 2015. No. 48, pp. 2–14.
- Toroptsev Ye.L., Marakhovskiy A.S., Duzhinski R.R. The problem of digitizing the dynamic model of the input-output balance [Problema otsifrovki dinamicheskoy modeli mezhotraslevogo balansa]// Economic analysis: theory and practice. – 2020. – T. 19, No. 5. – P. 946 – 972. https://doi.org/10.24891ea.19.5.946
