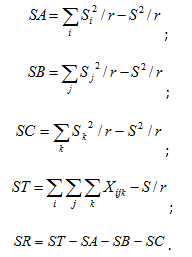Интернет вещей как глобальная инфраструктура для информационного общества
Введение
На теорию управления существенное влияние оказывают научные технологические достижения. По мнению Е.И. Кудрявцева важным фактором современного развития управленческой деятельности выступают распределенные информационные технологии [1]. Одним из подходов, реализующим распределенное управление являются сетевые системы и технологии. Одной из таких технологий и систем является технология Интернет вещей. Появление этой технологии как нового этапа глобального технологического развития связано и обусловлено динамичным внедрением информационно-коммуникационных технологий во все сферы жизни общества [2]. Эта технология проявляется прежде всего в быстрорастущей цифровой экономике [2], опирающейся на массовое использование технологий Интернет, достижений микроэлектроники и программной инженерии. Интернет- вещей и решения на их основе часто называют «умными» (smart) [3]. Сегодня они наиболее широко представлены в таких областях, как «умное производство», «умная энергетика», «умная агрокультура», «умная логистика», «умный транспорт», «умный дом», «умный город», «умное здравоохранение» и этот перечень, очевидно, будет только расти, охватывая все новые рыночные сегменты
Концептуальные основы технологии Интернет вещей
Интернет вещей (Internet of things — IoT) основана на межсетевом информационном взаимодействии [4] взаимодействие физических устройств, транспортных средств (также называемых «подключенными устройствами» и «интеллектуальными устройствами»), зданий и других предметов, встроенных в электронику, программное обеспечение, датчики, исполнительные механизмы и сеть, которые позволяют этим объектам собирать и обмениваться данными [5].
В 2013 году Глобальная инициатива по стандартизации в Интернете вещей (IoT-GSI) определила IoT как «глобальную инфраструктуру для информационного общества, предоставляющую расширенные услуги путем объединения (физических и виртуальных) вещей на основе существующих и развивающихся интероперабельных информационно-коммуникационные технологий» [3] и для этих целей «вещью» является «объект физического мира (физические вещи) или информационный мир (виртуальные предметы), который может быть идентифицирован и интегрирован в коммуникационные сети» [6]. Интернет вещей позволяет объектам быть обнаруженными или контролируемыми удаленно через существующую сетевую инфраструктуру, создавая возможности для более прямой интеграции физического мира в компьютерные системы и в результате повышая эффективность, точность и экономическую выгоду в дополнение к сокращению вмешательства человека.
В случае, когда IoT дополняется сенсорами и приводами, эта технология становится основой более общего класса кибер- физических систем, который также включает такие технологии, как smart-сети, виртуальные электростанции, интеллектуальные дома, интеллектуальный транспорт и интеллектуальный город . Каждая вещь уникально идентифицируется через встроенную вычислительную систему и при этом способна взаимодействовать с существующей инфраструктурой Интернета. По оценкам экспертов, к 2020 году IoT будет состоять из 30 миллиардов объектов [7].
Сферу интернет-вещей образуют разнообразные устройства и их пользователи, находящиеся в онлайн взаимодействии, включая мобильные коммуникации. Предполагается, что к 2020 году на каждого человека в среднем будет приходится 6 разных устройств в режиме он-лайн: компьютеры, мобильные телефоны, смартфоны, фаблеты и планшеты, устройства для дома, контроля показателей здоровья и т.д.
Согласно [8] к 2021 году существенно возрастет число мобильных умных устройств (smart devices) и объем генерируемого ими трафика. К мобильным умным устройствам принято относить устройства, обладающие развитыми вычислительными возможностями и мультимедиа со скоростью сетевого соединения, как минимум, на уровне 3G, т.е. 2 Мб/с. В 2016 году эти устройства, представляя лишь 46% всех мобильный устройств генерировали 89% мобильного трафика, а к 2021 году они составят три четверти от общего числа, и доля их трафика возрастет до 98 %.
Вторым по значимости сегментом являются устройства межмашинного взаимодействия, кратко обозначаемые как М2М (Machines to Machines). Надо отметить, что давно известные промышленные системы автоматического управления и телеметрии, реализующие замкнутые взаимодействия типа вещь-вещь, по сути являются предосновой интернета-вещей. Однако, если ранее были ограничения рамками одного локально расположенного производственного участка, цеха или предприятия, то сегодня появилась возможность выхода в Интернет. Это радикально расширяет сферу М2М, практически снимая территориальные ограничения. Здесь прогнозируется рост с 780 млн в 2016 году до 3,3 млрд в 2021 году. Подробные сценарии и примеры использования современных решений М2М в различных отраслях приведены в техническом отчете ведущей международной организации по стандартизации в этой области oneM2M [9].
В сегменте М2М отдельную категорию составляют носимые вещи (smart wearable devices): умные часы, умные очки и т.д. Такие вещи или напрямую взаимодействуют с сотовыми сетями и Интернет или посредством смартфонов и других устройств общего назначения. Ожидается рост этого сегмента до 929 млн устройств в 2021 году против 325 млн в 2016 году.
Современные цифровые методы порождают огромные объемы данных, которые приводят к проблеме больших данных [10]. В [11] приводятся характерные показатели: датчики реактивного двигателя каждые 30 мин генерируют 104 ГБ информации, ежедневно в мире датчики выдают 1,1 млрд показаний и производится 2,5 млрд ГБ данных. Первичные данные требуют обработки, в ряде случаев с привлечением сложной аналитики и ранее накопленной информации. Такая обработка не всегда может быть выполнена вблизи источника данных, например, вследствие отсутствия необходимых вычислительных и/или программных ресурсов. Поэтому в последнее время широко применяются технологии Облачных вычислений, реализующие услуги типа «Программное обеспечение как услуга» (SaaS), а при необходимости и «Сеть как услуга» (NaaS).
Решения IoT активно внедряются во все отрасли производства и сферы жизнедеятельности. Основные из них на данный момент — это решения для умного дома и города, энергетики, транспорта и логистики, ритейла и потребительского рынка, добычи и переработки полезных ископаемых, здравоохранения и телемедицины, сельского хозяйства, комплексной безопасности.
Теоретические принципы управления с использованием Интернет вещей
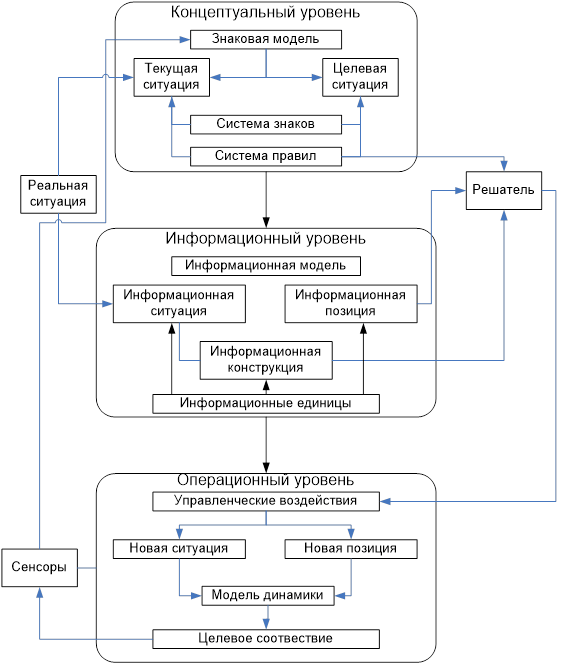
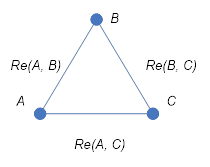
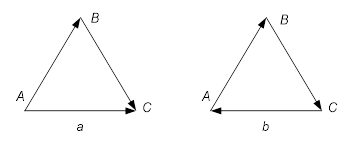
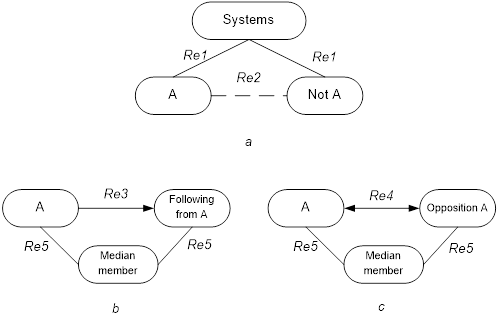
Управление с использованием Интернет вещей основано на информационном и сетевом моделировании, а также на различных информационных моделях. В настоящее время появились новые понятия в области распределенного управления [12]. Это: информационные единицы [13, 14], информационные отношения [15], информационные конструкции [16] и информационные ситуации [17]. Информационные единицы являются базисом построения информационных моделей, информационных конструкций и информационных процессов. Информационная конструкция является обобщением специализации. Она делиться на две категории: процессуальная и структурная. Процессуальная информационное конструкция описывает правило или функцию управления. Структурная информационная конструкция описывает систему, модель или набор данных. Процессуальные информационные конструкции служат основой выводов и принятия решений. Информационные отношения создают основу качественного анализа и качественных рассуждений.
Направления применения IoT
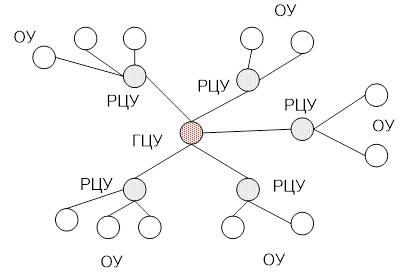
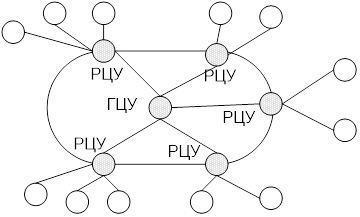
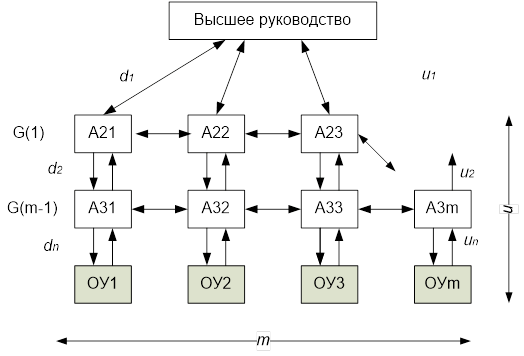
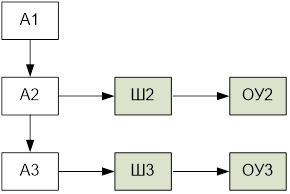
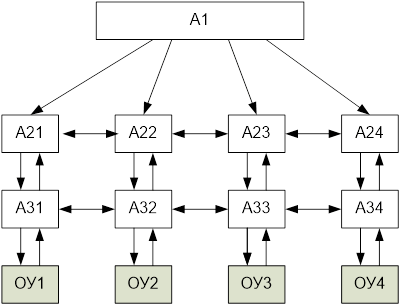
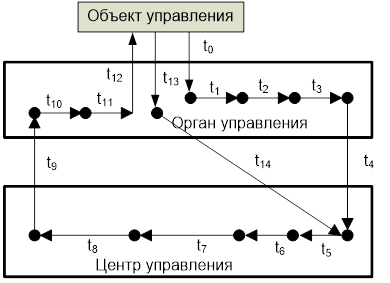
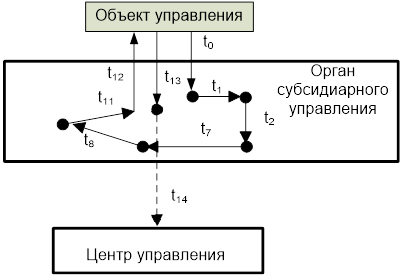
Можно выделить следующие аспекты, которые необходимо учитывать при применении интернет вещей: системный, проектный, информационный, управленческий, интеллектуальный. Системный аспект позволяет рассматривать систему, технологию или процесс с системных позиций. С этих позиций IoT является распределенной системой, для которой характерны проблемы распределенных систем. Проектный аспект позволяет рассматривать схему IoT как информационную конструкцию [16. 18]. Информационный аспект позволяет рассматривать IoT как межсетевое взаимодействие физических устройств, транспортных средств (также называемых «подключенными устройствами» и «интеллектуальными устройствами»), зданий и других предметов, встроенных в электронику, программное обеспечение, датчики, исполнительные механизмы и сеть, которые позволяют этим объектам собирать и обмениваться данными. Управленческий аспект требует рассматривать IoT как систему с сетецентрическим [19] или с субсидиарным управлением.
Интеллектуальный аспект требует разделения IoT по функциям на «умные» и «интеллектуальные». Умные (smart) системы и технологии, выполняют функции поддержки и «подсказки» человеку в сложных ситуациях. По существу они используют знания как опыт для решения задач в сложных ситуациях. Интеллектуальные системы и технологии используют знание для поиска новых решений и получения новых знаний на этой основе.
Впервые концепция IoT получила применение в 1999 году в Центре автоидентификации (Auto-ID Center) в Массачусетском технологическом институте. Радиочастотная идентификация (RFID ) была выделена Кевином Эштоном как предпосылка для Интернета вещей в этот момент [20]. При этом Эштон предпочитал фразу «Интернет для вещей». Основная идея идентификации состояла в том, что если бы все объекты и люди в повседневной жизни были снабжены идентификаторами, то компьютеры могли бы управлять и инвентаризировать их. Помимо использования RFID, маркировка физических вещей может быть достигнута с помощью таких технологий, как ближняя связь, штрих-коды, QR-коды и цифровые водяные знаки. Одной из первых целей внедрения Интернета вещей путем оснащения всех объектов в мире миниатюрными устройствами идентификации было преобразование повседневной жизни, например, мгновенный и непрерывный контроль запасов станет доступным рядовому потребителю.
Массмедиа. Было сделано предположение, что данные в средствах массовой информации являются большими данными [10] и дают возможность оценки практических действий о миллионах людей. Как следствие, воздействие на общество отодвигается от традиционного подхода использованию конкретных медиа-сред, таких как газеты, журналы или телевизионные шоу. Эта технология воздействия на массы вообще. Вместо этого IoT использует потребителей с технологиями, которые достигают целевых потребителей в оптимальное время в оптимальных местах. Конечной целью IoT является обслуживание или передача сообщения или контента, которые статистически соответствуют менталитету потребителя. Например, издательская среда все чаще приспосабливает сообщения (рекламные объявления) и контент (статьи), чтобы обратиться к потребителям, сведения о которых были получены благодаря различным действиям по ведению данных о них. Например, интеллектуальные торговые системы могут отслеживать покупательские привычки конкретных пользователей в магазине, путем фиксации их мобильных телефонов. Тематическая база данных потребителей на этой основе формирует специальные предложения по любимым продуктам или даже расположение необходимых предметов, которые им нужны, путем автоматического сообщения в телефон [21]. Эта технология является типичным примером smart технологии IoT.
Мониторинг окружающей среды. В приложениях мониторинга окружающей среды IoT используют датчики для оценки состояния окружающей среды, контролируя качество воздуха или воды, атмосферные или почвенные условия. Технологии IoT могут включать такие области, как мониторинг перемещений живой природы и среды их обитания. Разработка устройств с ограниченными ресурсами, подключенных к сети, создает возможность раннего предупреждения о оползнях или цунами. Разработка систем датчиков оповещения может использоваться аварийными службами для обеспечения более эффективной помощи. IoT-устройства в таких приложениях занимают большую географическую область и могут также мобильными.
Управление инфраструктурой. Важным применением IoT, как распределенной системы управления , является распределенный мониторинг и контроль операций городских, транспортных и сельских инфраструктур. Инфраструктура IoT может использоваться для мониторинга любых событий или изменений, которые представляют угрозу безопасности или увеличивают риск. Он также может использоваться для эффективного планирования ремонтных работ, координируя задачи между поставщиками услуг и пользователями этих объектов [22]. IoT-устройства могут также использоваться для управления критической инфраструктурой, такой как мосты, для обеспечения доступа к судам. Использование устройств IoT для мониторинга и операционной инфраструктуры улучшает координацию управления инцидентами и реагирование на чрезвычайные ситуации. Использование устройств IoT повышает качество обслуживания, времени простоя и сокращения затрат на эксплуатацию во всех областях, связанных с инфраструктурой.
В 2013 году Глобальная инициатива по стандартизации в Интернете вещей (IoT-GSI) определила IoT как глобальную инфраструктуру для информационного общества, предоставляющую расширенные услуги путем объединения (физических и виртуальных) вещей на основе Существующие и развивающиеся интероперабельных систем.
Производство. Сетевое управление и управление производственным оборудованием, управление активами и ситуациями или управление производственным процессом приносят IoT в сферу промышленного применения и интеллектуального производства. Интеллектуальные системы IoT позволяют быстро создавать новые продукты, динамически реагировать на требования к продуктам и оптимизировать производственную цепочку и сеть цепей поставок в режиме реального времени с помощью сетевого оборудования, датчиков и систем управления [22].
Цифровые системы управления для автоматизированного управления процессами, инструментами оператора и информационными системами обслуживания для оптимизации безопасности и безопасности станции относятся к компетенции IoT. Технологии IoT также распространяются на управление активами посредством прогнозирования обслуживания, статистической оценки и измерений для обеспечения максимальной надежности. Интеллектуальные промышленные системы управления также могут быть интегрированы в Smart Grid, что позволяет оптимизировать энергопотребление в реальном времени. Измерения, автоматизированные системы управления, оптимизация установок, управление безопасностью и охраной труда и другие функции обеспечиваются большим количеством сетевых датчиков [22].
Термин IIoT (Industrial Internet of Things) часто встречается в обрабатывающих отраслях, ссылаясь на промышленный поднабор IoT. IIoT в обрабатывающей промышленности может генерировать столько бизнес-ценности, что в конечном итоге приведет к четвертой промышленной революции, так называемой Industry 4.0 . По оценкам, в будущем успешные компании смогут увеличить свои доходы за счет использования Интернета, создавая новые бизнес-модели и повышая производительность, используя аналитику для инноваций и трансформируя трудовые ресурсы.
Управление энергопотреблением. Интеграция управляющих систем, подключенных к Интернету, может оптимизировать потребление энергии в целом [22]. Ожидается, что устройства IoT будут интегрированы во все виды энергопотребляющих устройств (переключатели, розетки питания, лампы, телевизоры и т. д.). Устройства IoT смогут общаться с компанией-поставщиком энергоснабжения, чтобы эффективно сбалансировать производство электроэнергии. Такие устройства также предоставляют пользователям возможность удаленно управлять своими устройствами или централизованно управлять ими с помощью облачного интерфейса и включать такие расширенные функции, как планирование (например, дистанционное включение или выключение систем отопления, управление духовыми шкафами, изменение освещения и т. д.) [22].
Помимо домашнего управления энергией, IoT актуален для Smart Grid, так как он предоставляет системы для сбора и обработки информации об энергии и мощности в автоматическом режиме с целью повысить эффективность, надежность, экономичность и устойчивость производства и распределение электроэнергии. Используя устройства расширенной измерительной инфраструктуры, подключенные к магистральной сети Интернет, электрические утилиты могут не только собирать данные от конечных пользователей, но также управлять другими устройствами распределения, такими как трансформаторы и реклоузеры [22].
Медицина и здравоохранение. Устройства IoT могут использоваться для дистанционного мониторинга состояния и систем аварийного оповещения о состоянии пациентов. Специализированные датчики в жилых помещениях для наблюдения за состоянием здоровья и общего благополучия пожилых людей, а также для обеспечения надлежащего лечения и оказания помощи людям в восстановлении утраченной мобильности с помощью терапии. Эти устройства мониторинга работоспособности могут варьироваться от мониторов артериального давления и частоты сердечных сокращений до современных устройств, способных отслеживать специализированные имплантаты, такие как электронные кардиостимуляторы Fitbit или усовершенствованные слуховые аппараты [22].
Некоторые больницы начали внедрять «умные кровати», которые могут определять, когда они заняты и когда пациент пытается встать. Он может также регулировать себя, чтобы обеспечить соответствующее давление и поддержку, применяемую к пациенту без вмешательства медсестер вручную. С IoT также возможны другие потребительские устройства для стимулирования здорового образа жизни, такие как связанные весы или переносные мониторы сердца [86]. Все больше и больше сквозных мониторингов здоровья Платформы IoT подходят для антенатальных и хронических пациентов, помогая управлять жизненными функциями и повторяющимися потребностями в медицине.
Строительная и бытовая автоматизация. Устройства IoT могут использоваться для мониторинга и контроля механических, электрических и электронных систем, используемых в различных типах зданий (например, государственных и частных, промышленных, учебных заведений или жилых помещений) [22] в системах домашней автоматизации и автоматизации зданий. В этом контексте в литературе рассматриваются три основные области [23].
Интеграция интернета с системами энергоменеджмента зданий для создания энергоэффективных и интеллектуальных зданий, управляемых IOT.
Возможные средства мониторинга в режиме реального времени для снижения потребления энергии и мониторинга поведения пассажиров.
Интеграция интеллектуальных устройств во встроенную среду и то, как они могут использоваться в будущих приложениях.
IoT может помочь в интеграции средств связи, управления и обработки информации в различных транспортных системах. Применение IoT распространяется на все аспекты транспортных систем (т.е. транспортного средства, инфраструктуры и водителя или пользователя). Динамическое взаимодействие между этими компонентами транспортной системы обеспечивает внутри автомобильную связь, интеллектуальное управление трафиком, интеллектуальную парковку, электронные системы взимания дорожных сборов, логистику и управление автопарком, управление транспортным средством, безопасность и помощь на дороге [22].
Заключение
Интернет вещей является новой сетевой технологией управления основанной на распределении датчиков и физических устройств в объекте управления. Интернет вещей содержит несколько принципиально новых технологических решений, которые не содержат другие системы управления. Прежде всего, это возможность реконфигурирования управленческих информационных потоков в зависимости от трафика и нагрузки на узлы сети. Интернет вещей содержит интеллектуальные узлы, которые позволяют реализовывать распределенное управление. Интернет вещей содержит собственные вычислительные ресурсы. которые позволяют решать задачи оптимизации. Не прибегая к мощным центральным компьютерам. Интеллектуальные ресурсы Интернет вещей позволяют накапливать управленческий опыт и применять его в новых ситуациях.
Библиографический список:
- Кудрявцева Е. И. Психология управленческой эффективности в условиях распределенного управления //Управленческое консультирование. – 2013. – №. 9 (57). – с.22-32.
- Зеленин Д. В., Логинов Е. Л. Новая парадигма управления экономикой: переход к “умным сетям” различного управленческого назначения //Экономические науки. – 2010. – Т. 70. – №. 9. – С. 156-161
- Internet of things. https://en.wikipedia.org/wiki/Internet_of_things. Дата доступа 17.05.2017
- Tsvetkov V. Yа. Information interaction // European researcher. Series A. 2013. № 11-1 (62). С. 2573-2577/
- Brown, Eric (13 September 2016).»Who Needs the Internet of Things?» Linux.com
- International Telecommunication Union, Overview of the Internet of things, Recommendation ITU-T Y.2060, June 2012
- Nordrum, Amy (18 Aug 2016).»Popular Internet of Things Forecast of 50 Billion Devices by 2020 Is Outdated». IEEE.
- International Telecommunication Union, Overview of the Internet of things, Recommendation ITU-T Y.2060, June 2012
- Technical Report oneM2M Use Case collection. Режим доступа: http://www.etsi.org/deliver/etsi_tr/118500_118599/118501/01.00.00_60/tr_118501v010000p.pdf (дата обращения 06.03.2017).
- Чехарин Е.Е. Большие данные: большие проблемы // Перспективы науки и образования. — 2016. — №3. — с.7-11.
- The Internet of Things. Режим доступа: https://www.cisco.com/web/offer/emear/38586/images/Presentations/P11.pdf (дата обращения 06.03.2017).
- Цветков В. Я. Распределенное управление// Современные технологии управления. -2017. — №3(75). Режим доступа: https://sovman.ru/article/7602/
- Романов И.А. Применение информационных единиц в управлении// Перспективы науки и образования- 2014. — №3. – с.20-25.
- Tsvetkov V. Ya. Information Units as the Elements of Complex Models // Nanotechnology Research and Practice. — 2014, Vol.(1), № 1, р57-64
- V. Ya. Tsvetkov. Information Relations // Modeling of Artificial Intelligence, 2015, Vol.(8), Is. 4. – р.252-260. DOI: 10.13187/mai.2015.8.252 www.ejournal11.com
- Tsvetkov V. Ya. Information Constructions // European Journal of Technology and Design. -2014, Vol (5), № 3. — p.147-152
- Ожерельева Т.А. Информационная ситуация как инструмент управления // Славянский форум, 2016. -4(14). – с.176-181.
- Дешко И.П. Информационное конструирование: Монография. – М.: МАКСПресс, 2016. – 64с. ISBN 978 -5-317-05244-7
- Кудж С.А. Принципы сетецентрического управления в информационной экономике // Государственный советник. – 2013. — №4. – с30-33.
- Magrassi, P. (2 May 2002). «Why a Universal RFID Infrastructure Would Be a Good Thing». Gartner research report G00106518.
- CasCard; Gemalto; Ericsson. «Smart Shopping: spark deals»(PDF). EU FP7 BUTLER Project.
- Ersue, M.; Romascanu, D.; Schoenwaelder, J.; Sehgal, A. (4 July 2014). «Management of Networks with Constrained Devices: Use Cases». IETF Internet Draft.
- Swan, Melanie (8 November 2012). «Sensor Mania! The Internet of Things, Wearable Computing, Objective Metrics, and the Quantified Self 2.0». Sensor and Actuator Networks. 1 (3): 217–253. doi:10.3390/jsan1030217.
Интернет вещей как глобальная инфраструктура для информационного общества Читать далее »












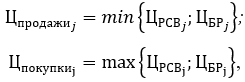
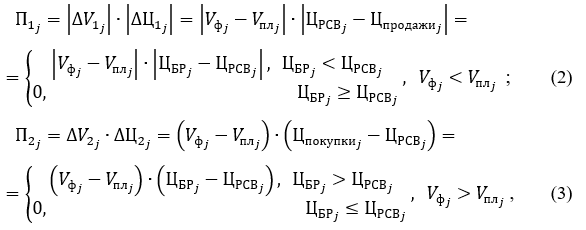

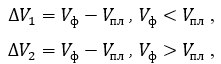







 , (1)
, (1)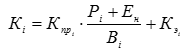 , (3)
, (3)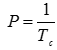 , (4)
, (4)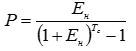 , (5)
, (5)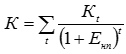 , (6)
, (6)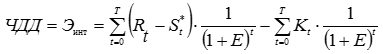 , (7)
, (7)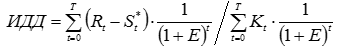 , (8)
, (8)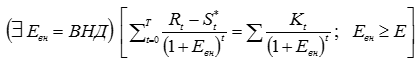 , (9)
, (9)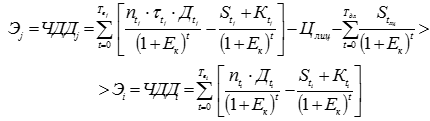 , (10)
, (10)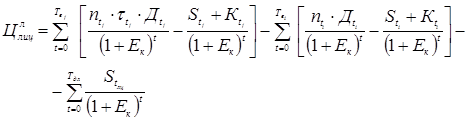 , (11)
, (11)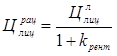
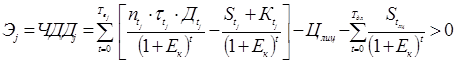 , (13)
, (13)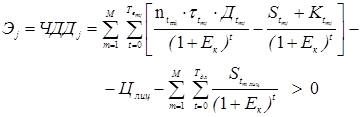 , (14)
, (14)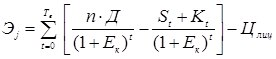
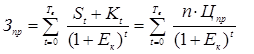 , (16)
, (16)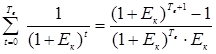 , (17)
, (17)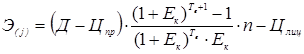 , (18)
, (18)